Splay 树：均摊时间下的平衡二叉搜索树

Splay 树的基本定义

关于平衡二叉搜索树，我们介绍过 AVL 树。AVL 树通过旋转来保证了相对严格的自平衡，这样操作复杂度是 O(logN)。

今天我们要介绍的 Splay 树也是一个平衡二叉树，但是它并没有像 AVL 树那样去严格地保证树的平衡性，每次当 AVL 树的结构发生变化，就找到相应的节点进行调整。对于 Splay 树来说，不管是什么样的操作，读、写、更新以及删除，Splay 树均会对树的结构进行调整，这个调整会通过类似 AVL 树的旋转的方式把被操作的节点给移到根节点处，在移动的过程中，树的整体结构被调整了，从而能保证 O(logN) 时间复杂度。但是这个时间复杂度是均摊时间复杂度，也就是说，对于连续的 M 个操作，Splay 保证最后的时间复杂度是 O(MlogN)，但是对于单一的操作，Splay 树并不保证 O(logN)。

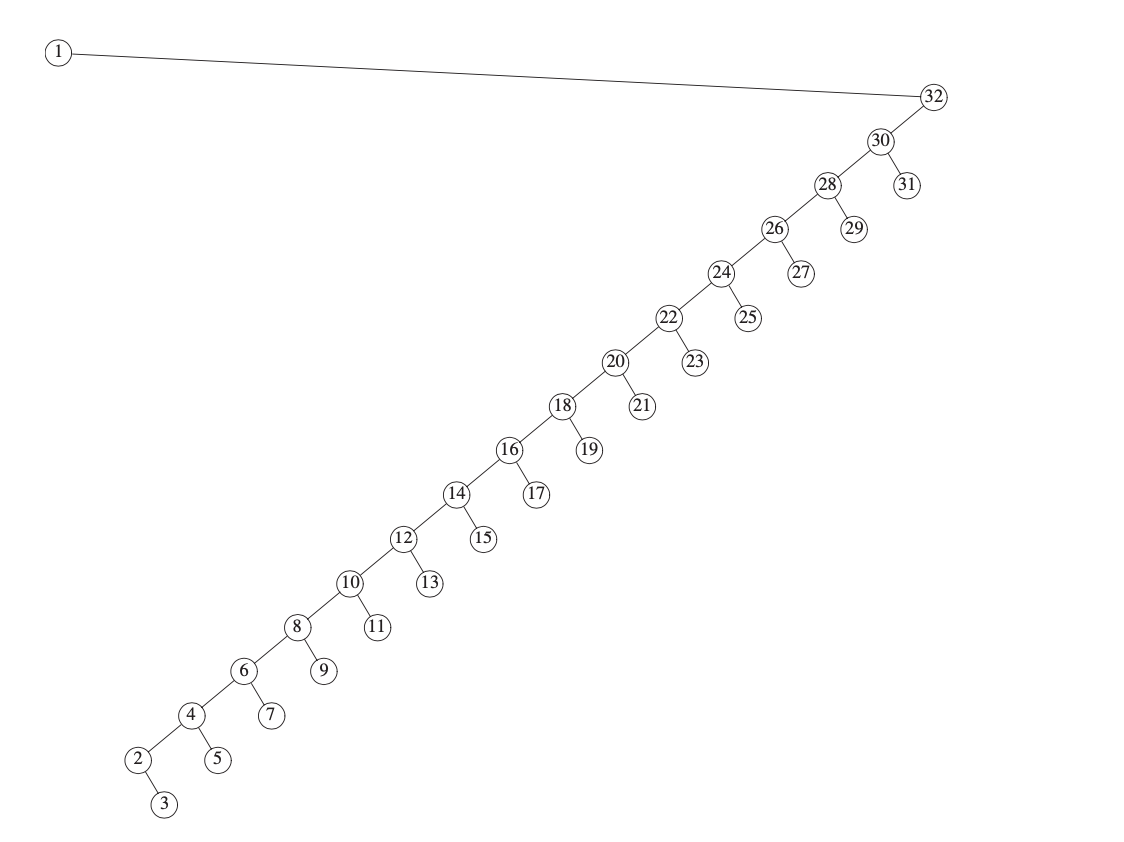
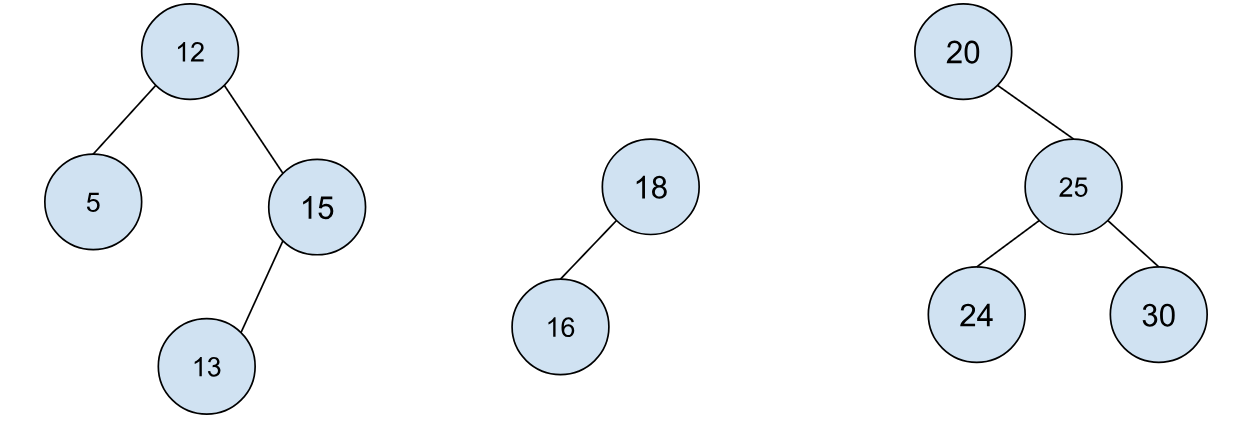
由于 Splay 树的对平衡性的定义，Splay 的结构并没有严格的规定，任何结构的树都可以是 Splay 树，让我们来看一个例子：

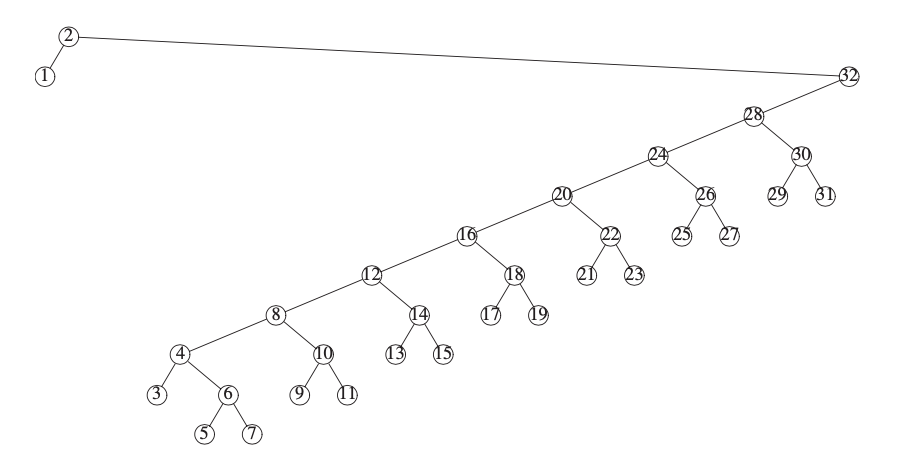
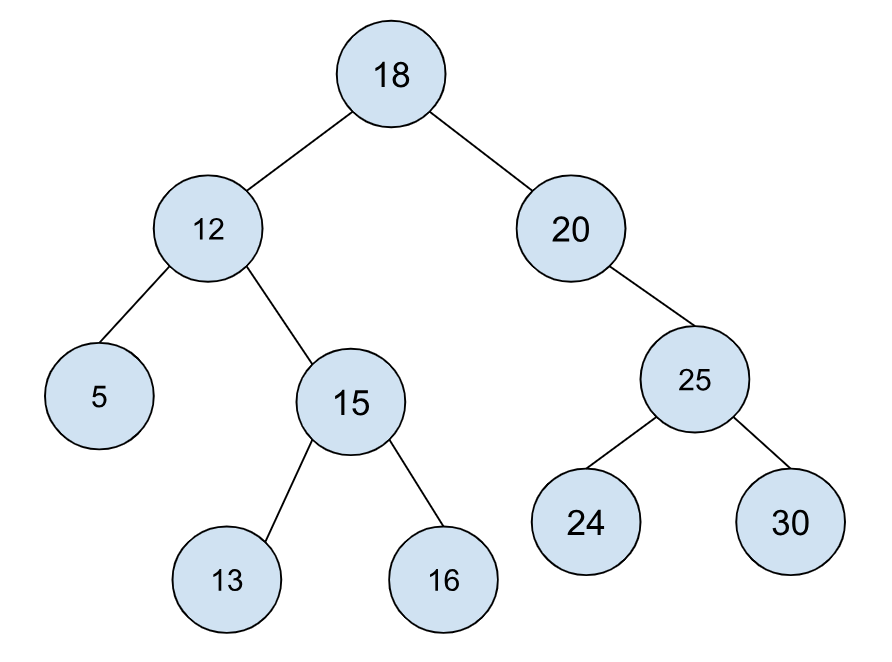
在这个例子中，当我们去获取 2 这个节点的信息，树的结构就会被调整成下图，可以很清晰地看到调整之后的树的整体的深度变小了，比如之前 4 这个节点要通过 16 次操作才能访问到，但是现在仅需 8 次操作：

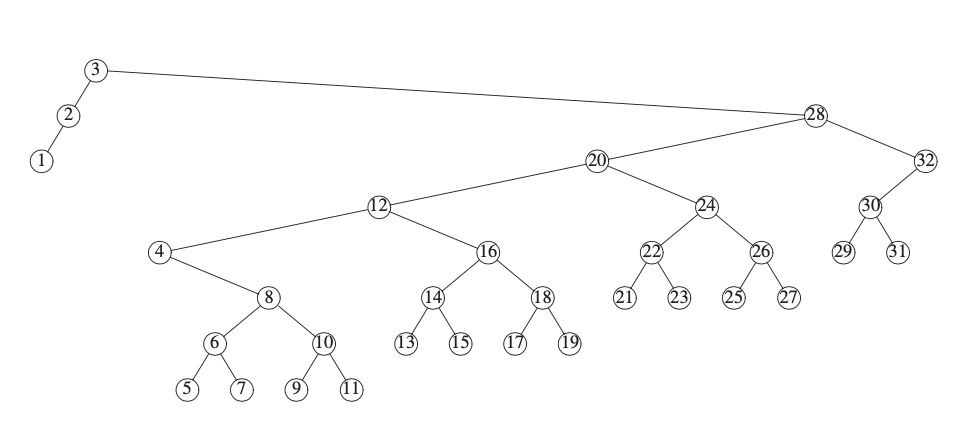
我们继续去获取 3 的节点信息，就会得到下图：

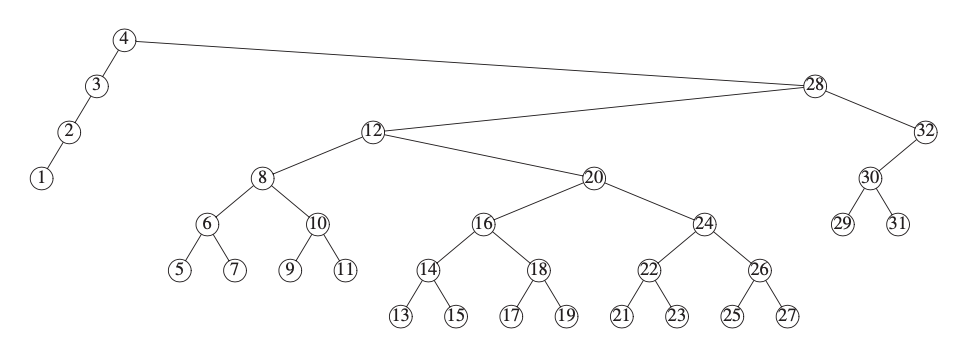
然后是获取 4 的节点信息：

通过上面这些图，我们可以直观地感受到 Splay 树并不仅仅针对某个节点或者某个子树进行调整，而是调整某个节点到根节点这条链上的所有节点，可以说是整个树的调整。而这样做有什么好处呢？

第一个好处就是简单直观，增删改查不会被区别对待，在后面的实现方式上，你也可以体会到这种简单。

第二个好处是在某些情况下，实际的时间开销会比较小。这个怎么理解呢？在实际生产中，当获取某个节点后，这个节点近期被再次获取的概率会很大，而 Splay 树把获取的节点移到根节点就会降低再次获取的时间。

Splay 树的实现

Splay 树的有多种实现方式，但是我们这次介绍的是一种 从上到下 的方式。就是当开始获取某个节点时，在向下寻找的过程中，我们就一遍定位，一边对树的结构进行调整。相比传统的 “找到节点，然后向上移动调整” 的方式，从上到下这种方式有 2 大好处：

• 我们不需要在节点中存放和维护额外的信息，诸如，父节点的引用，节点的高度等，实现会变的比较简单
• 在实际应用上，这种方式的运行效率更高，并且它也保证了 O(logN) 的均摊时间

旋转情况讨论

和 AVL 树类似，Splay 树也是通过旋转来对树节点进行移动和调整。其实 Splay 可以套用 AVL 树的旋转，但是这是对传统的从下往上的方式来说的。当我们选择了从上到下的调整方式，还需对其做一些改变，不然试想一下，你如何旋转才能将最后访问到的节点放到根节点上呢？

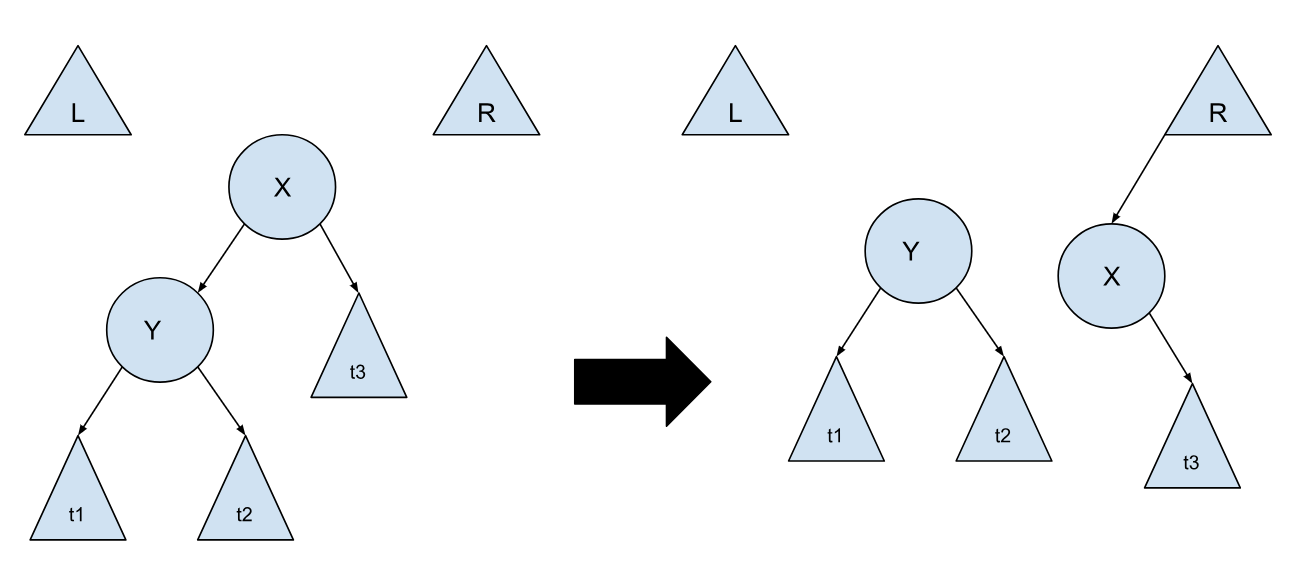
我们先来看第一种情况：

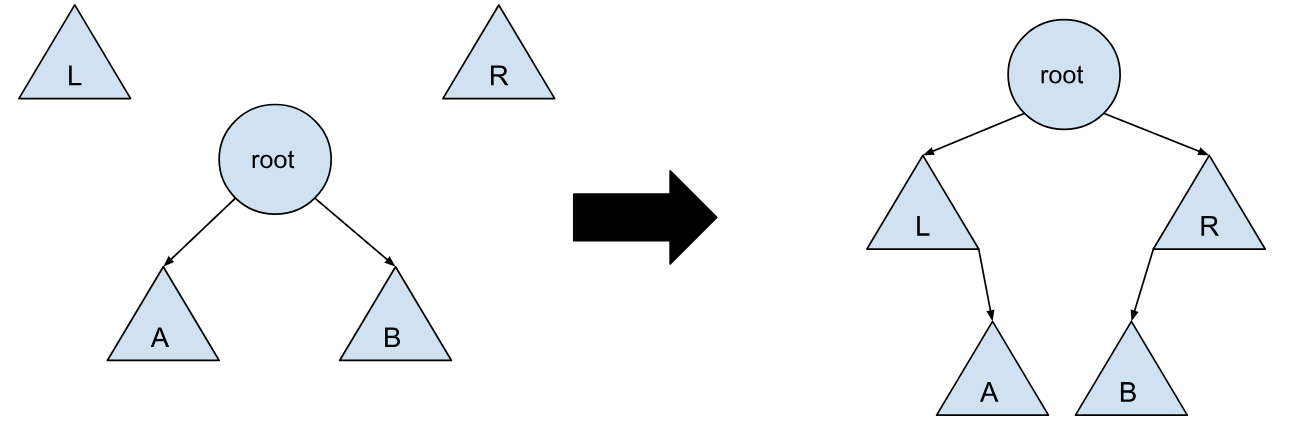
这里假设我们当前遍历到的节点是 X，我们需要去到 Y，我们想要做的是把 Y 的位置移到靠上面些。如果这里沿用之前的 AVL 树的旋转方式，势必树的结构会发生改变，从而导致接下来的遍历没法很好地进行。这里采取的措施是把以 Y 为根节点的这整颗树作为当前遍历的树，然后把 X 连同剩下的部分移到 R 下面。这里的 L 和 R 是我们创建出来的辅助树，L 存放的是树上比当前节点 X 小的部分，R 存放的是比当前节点 X 大的部分，在遍历开始时，L 与 R 均为空，在不断地向下遍历，不断地调整，L 与 R 上就会不断地有子树被加上。这种情况还有一个对称的情况，就是 Y 在 X 的右边，我们只需把 X 挂到 L 的最右边即可。

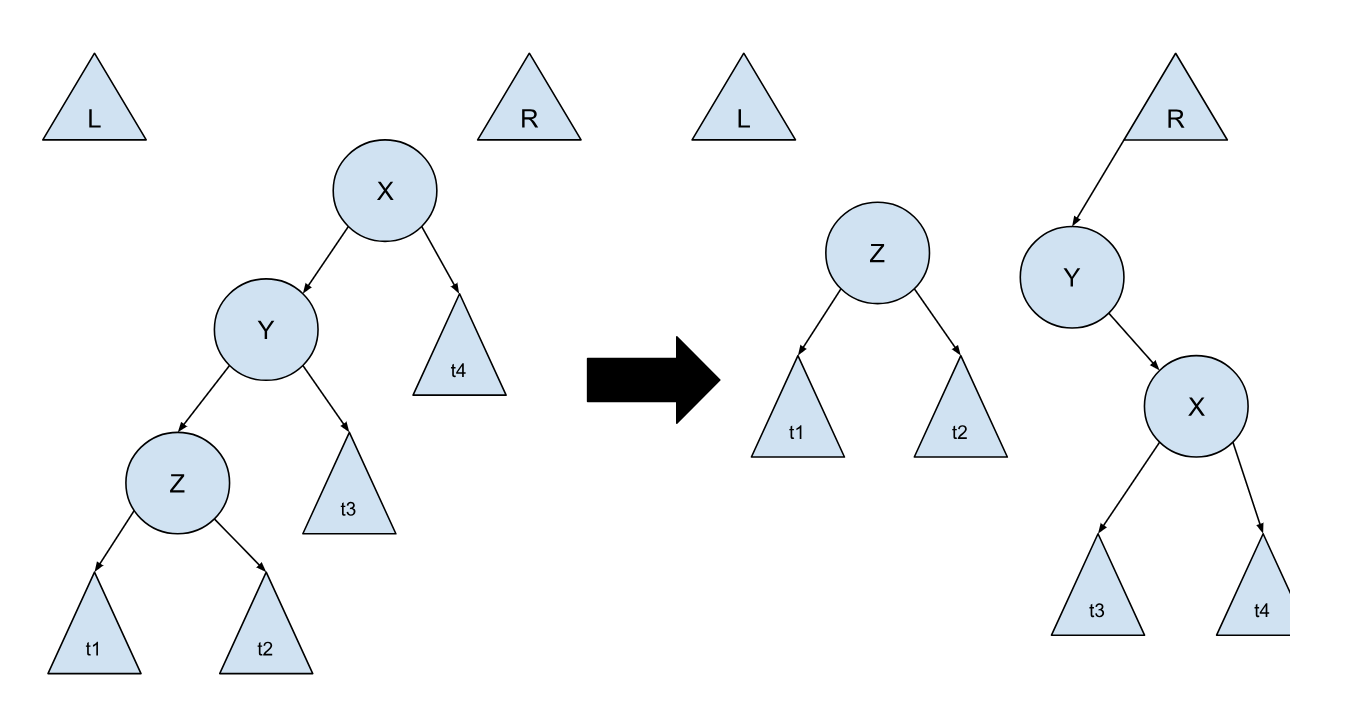
第二种情况和第一种很类似，不过这时我们需要去到更下面一层：

你可能会说，这种情况其实就是两次第一种情况啊，为什么要单独放出来讨论？因为如果都按照第一种情况，在特定的情况下并不能很好地压缩树结构，最后也就没法保证 O(logN) 的均摊时间。同理，和第一种情况一样，这里也有一个对称的情况，这里就不展开了，左右颠倒就好了。

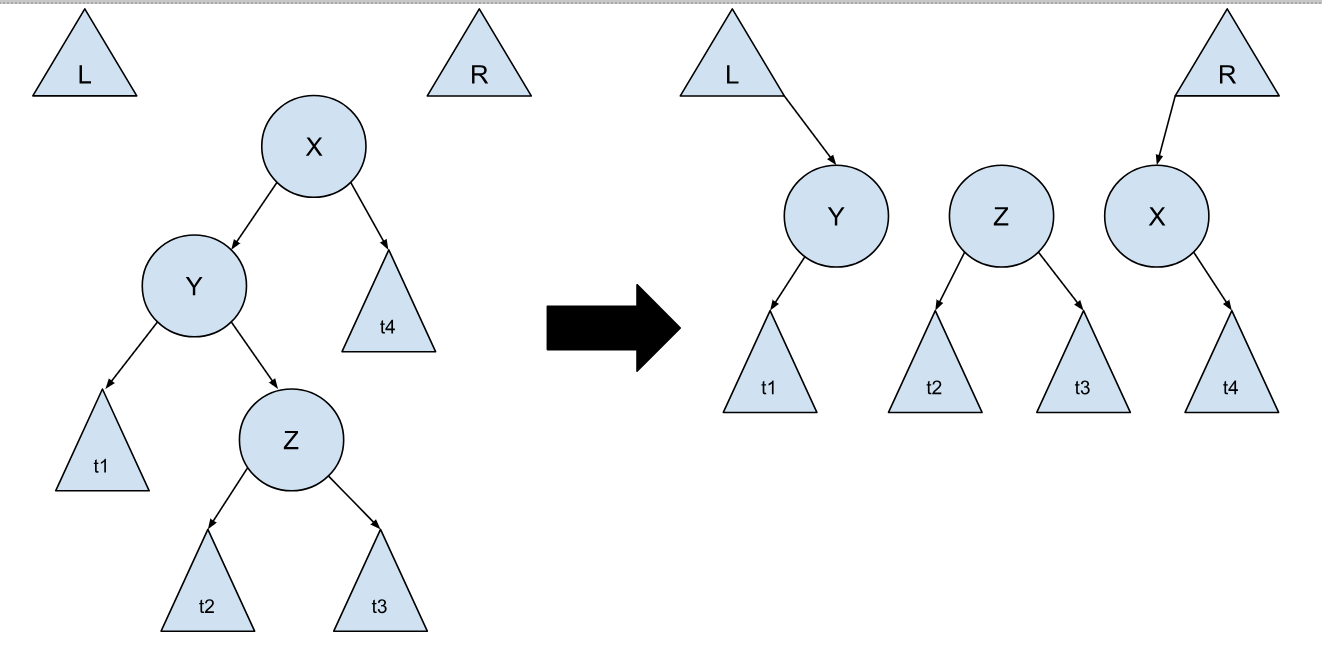
最后是第三种情况：

但其实这种情况，就是两个（对称的）第一种情况叠加而成的，我们只需将其看成是第一种情况就好了，不然情况太多，在实现的时候我们需要做很多的判断，这会增加代码的复杂度不说，还会影响程序的运行效率：

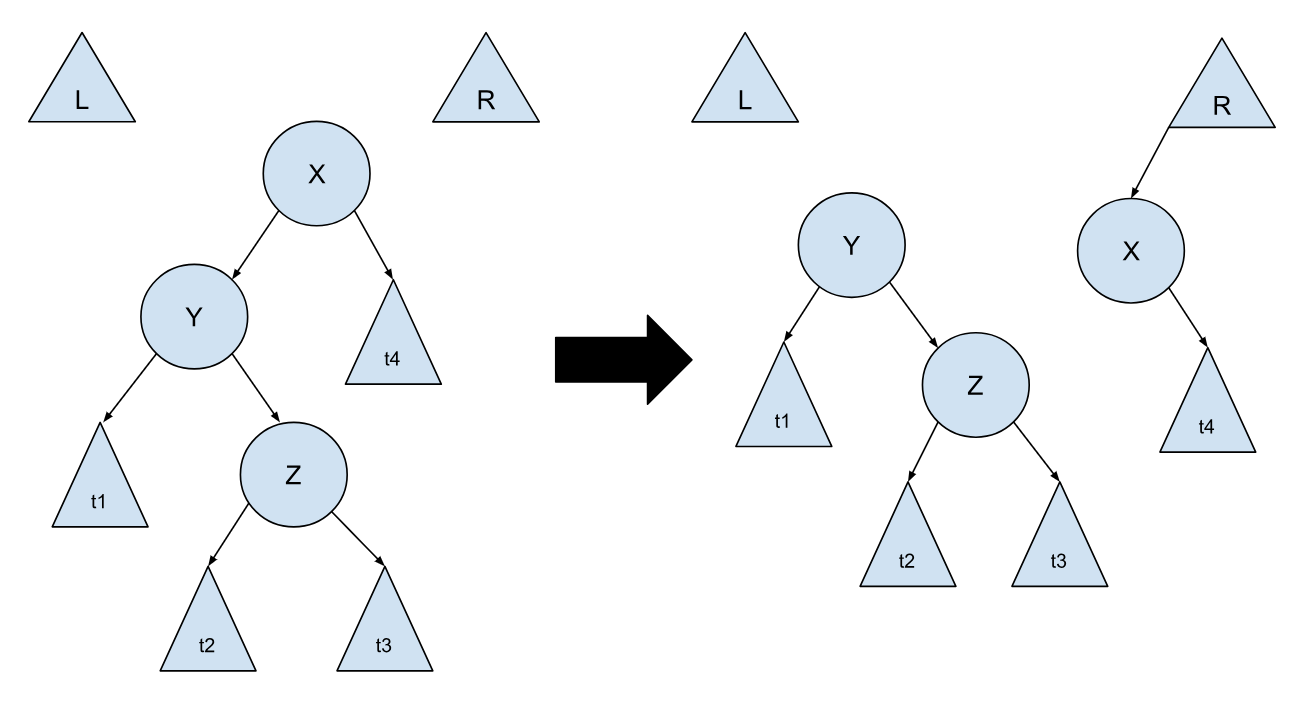
所以，整个旋转情况，其实就变成了 2 种（第一种与第二种）以及它们的对称情况。遍历到了最后，也就是找到了需要找的节点，我们还需要一个操作，就是将当前树与 L 树，还有 R 树进行合并，这个其实挺直观的，直接根据二叉搜索树的定义拼接起来即可：

这样，最后遍历到的节点就会成为新的树的根节点，在遍历的过程中，我们也依照相应的情况对树的结构进行了改变。

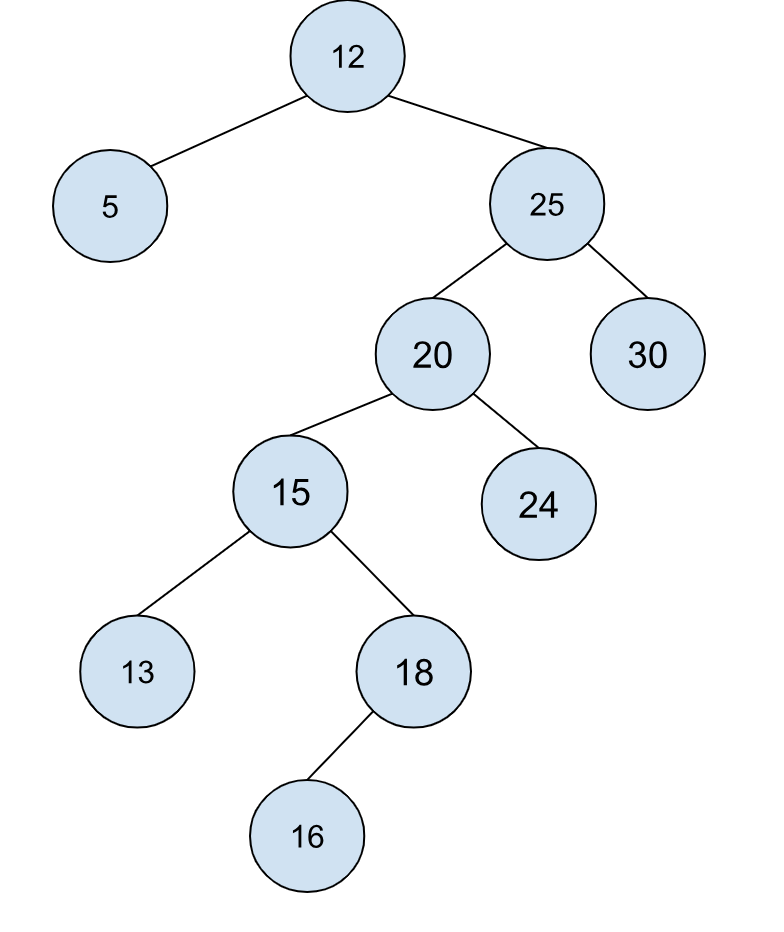
我们来看一个具体的案例，来体会一下这个算法给整个树带来的变化。有如下这颗树，我们想要查找值为 19 的树节点，一开始的时候我们的位置在根节点，也就是 12 处，两边的 L 与 R 树均为空：

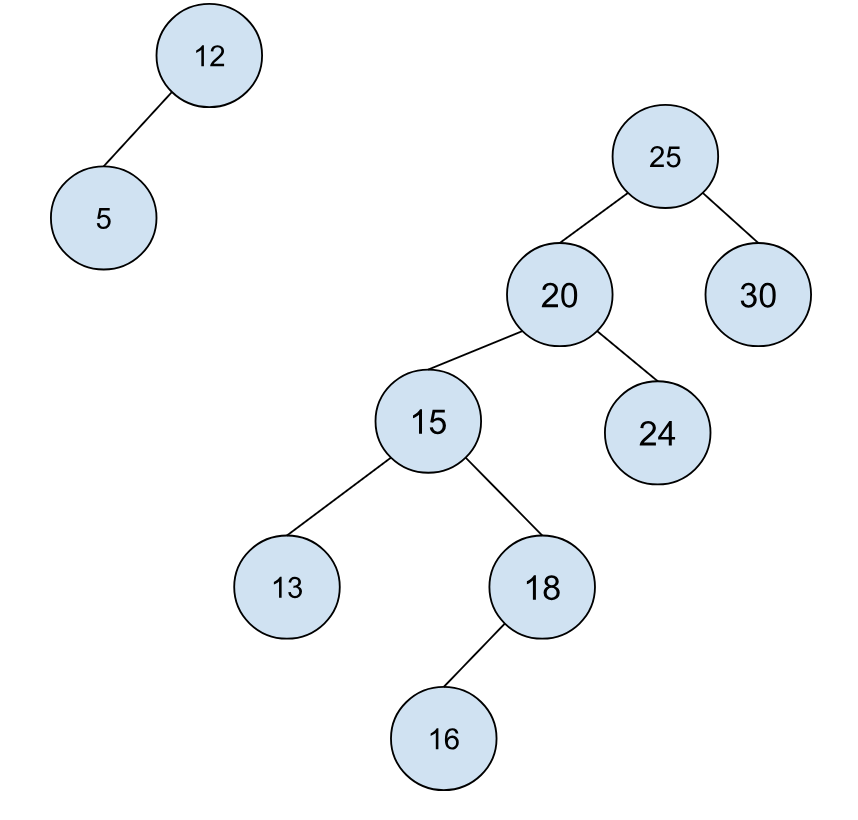
下一步我们要去的是节点 25，也就是我们之前讨论的第一种情况的对称情况，所以我们可以将树变成下面这样：

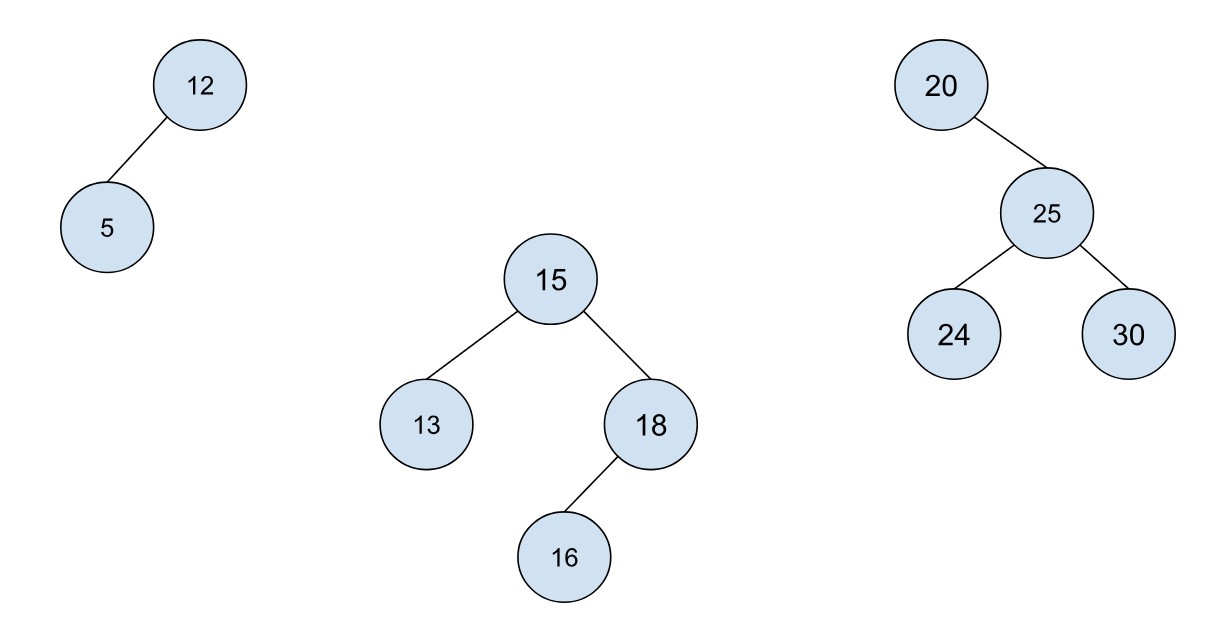
然后我们要去到节点 25，也就是我们之前讨论的第二种情况，旋转后可得：

最后我们要去到节点 18，这里还是第一种情况的对称情况，旋转可得：

虽然我们没有找到 19，但是我们的遍历终止在 18 处，这时我们进行最后的拼接就得到最后的树：

将变换后的树和原来的树比较，我们可以很容易看到树的深度被缩小了。

具体实现

在给出具体操作的实现前，我们先来定义一些辅助变量，这些辅助变量会让实现变得更加容易。

public class SplayTree<AnyType extends Comparable<? super AnyType>> {
  private class BinaryNode<AnyType> {
    BinaryNode(AnyType theElement) {
      this(theElement, null, null);
    }

    BinaryNode(AnyType theElement, BinaryNode<AnyType> lt, BinaryNode<AnyType> rt) {
      element = theElement;
      left = lt;
      right = rt;
    }

    AnyType element;
    BinaryNode<AnyType> left;
    BinaryNode<AnyType> right;
  }

  private BinaryNode<AnyType> root;
  private BinaryNode<AnyType> nullNode;
  private BinaryNode<AnyType> header = new BinaryNode<>(null);
  private BinaryNode<AnyType> newNode = null;
}

这里，我们定义了一个树节点 BinaryNode，就是普通的二叉树节点。紧接着，我们定义了几个变量，root 表示的是当前树的根节点，代表整颗树。nullNode 是一个哨兵节点，用来表示空，它可以简化代码。header 是用来存放我们上面讨论的 L 和 R 这两个中间生成的子树的。最后的 newNode 则是用来存放插入节点的，因为这里我们默认不重复插入相同的元素，这个变量可以看做是暂存。

查询

splay 树的查询操作是基础，它将我们需要查找的元素移到根节点处，以此同时树的结构也会发生改变

private BinaryNode<AnyType> splay(AnyType x, BinaryNode<AnyType> t) {
  BinaryNode<AnyType> leftTreeMax, rightTreeMin;

  header.left = header.right = nullNode;
  leftTreeMax = rightTreeMin = header;

  nullNode.element = x;

  while (true) {
    if (x.compareTo(t.element) < 0) {        // 情况一
      if (x.compareTo(t.left.element) < 0) { // 情况二
        t = rotateWithLeftChild(t);
      }
      if (t.left == nullNode) {
        break;
      }
      // 将遍历过的部分放到 R 上，以此同时在 R 的左子树上继续遍历
      // 也就是说 R 的左边空出来用于下次存放
      rightTreeMin.left = t;
      rightTreeMin = t;
      t = t.left;
    } else if (x.compareTo(t.element) > 0) {  // 情况一的对称情况
      if (x.compareTo(t.right.element) > 0) { // 情况二的对称情况
        t = rotateWithRightChild(t);
      }
      if (t.right == nullNode) {
        break;
      }
      leftTreeMax.right = t;
      leftTreeMax = t;
      t = t.right;
    } else { // 找到目标元素，停止查找
      break
    }
  }

  // 最终整合
  leftTreeMax.right = t.left;
  rightTreeMin.left = t.right;
  t.left = header.right;
  t.right = header.left;

  return t;
}

//      t          tl          t          tl   
//     / \     ->  / \    ->  / \    ->   / \  
//    tl  tr     tll tlr     tlr tr     tll  t
//   / \                                    / \
// tll tlr                                 tlr tr
private BinaryNode<AnyType> rotateWithLeftChild(BinaryNode<AnyType> t) {
  BinaryNode<AnyType> tl = t.left;
  t.left = tl.right;
  tl.right = t;
  return tl;
}

private BinaryNode<AnyType> rotateWithRightChild(BinaryNode<AnyType> t) {
  BinaryNode<AnyType> tr = t.right;
  t.right = tr.left;
  tr.left = t;
  return tr;
}

代码其实就是将之前的 2 种情况及其对称情况加以实现，重点在于节点的旋转以及变量的交替。

插入

有了查询，插入无非是先查询看要插入的节点是否存在于树中，如果有的话将其放置到根节点，没有的话也将临近的元素放到根节点，剩下的就是拼接了：

public void insert(AnyType x) {
  if (newNode == null) {
    newNode = new BinaryNode<>(null);
  }
  newNode.element = x;

  // 如果此时的树为空，那么插入的元素就是根节点
  if (root == nullNode) {
    newNode.left = newNode.right = nullNode;
    root = newNode;
  } else {
    // 先做查找，将相同或者接近的元素放到根节点处
    root = splay(x, root);

    // 查找在 root 处停止，说明
    // root 左子树上的元素一定比 x 小，root 右子树上的元素一定比 x 大，否则会继续查找

    if (x.compareTo(root.element) < 0) {
      newNode.left = root.left;
      newNode.right = root;
      root.left = nullNode;
      root = newNode;
    } else if (x.compareTo(root.element) > 0) {
      newNode.right = root.right;
      newNode.left = root;
      root.right = nullNode;
      root = newNode;
    } else {
      return;    // 为了保证树上没有重复的元素，直接返回
    }
  }

  // 将中间变量置空以便下次插入
  newNode = null;
}

删除

和插入操作类似，删除操作也是借助查询操作将对应的节点放置到根节点处。如果要删除的元素不存在，直接跳过。如果要删除的元素存在，直接将根节点删除，然后在左子树或者右子树中找一个元素来当作新的根节点：

public void remove(AnyType x) {
  BinaryNode<AnyType> newTree;

  root = splay(x, root);

  // 没有找到，直接返回
  if (root.element.compareTo(x) != 0) {
    return;
  }

  // 这里我们会在左子树中找一个最大的元素来当作根节点
  // 如果左子树为空，直接返回右子树
  if (root.left == nullNode) {
    newNode = root.right;
  } else {
    newTree = root.left;

    // 左子树中的所有元素均比 x 小，所以查询操作后新的左子树根节点一定是左子树中最大的
    // 其没有右子树，我们直接将删除操作后的右子树拼接到右边即可
    newTree = splay(x, newTree);
    newTree.right = root.right;
  }
  root = newTree;
}

splay 树的时间复杂度为均摊的 O(logN)，这个时间复杂度的证明需要复杂的数学公式推导，这部分内容我们以后找时间补上。