AVL树：古老的自平衡二叉搜索树

Posted Aug 3, 2023

By Yuhang Peng 13 min read

之前的文章介绍了什么是二叉搜索树，以及它的各项操作。但在代码实现的时候，只是给出了最简单的算法，并没有维持二叉搜索树的平衡。在极端情况下，二叉搜索树会退化为链表结构，从而导致搜索效率大幅下降，这是我们很不希望看到的。AVL 树就是一种自平衡二叉搜索树，也是最早的自平衡二叉搜索树，后面的很多平衡二叉树都是基于它来改进的，比如我们所熟知的红黑树，以及 splay 树等等。

AVL 树的基本定义

AVL 树的定义，其实是平衡性的定义。平衡这个概念，存在多种定义，AVL 树的平衡定义非常直接，每个节点的左右子树的高相差必须小于或等于 1。这个定义是比较严格的定义了，到 splay 树，平衡的定义又变了。

有人会对这个定义产生误解，认为整颗树上任意两个叶子节点的深度¹差也必须小于或等于 1。这个要求过于严厉了些，如果按照这个说法，二叉树得是一个完全二叉树或是满二叉树，这在实际的应用中难以达到。AVL 树的要求仅仅是每个节点的左右两颗子树的高相差 1 或等高即可，这一定要注意。

AVL 树的平衡性实现

之前的二叉搜索树的文章提到，树的结构的改变仅仅会发生在插入或删除操作，因为这些操作会增加或移除树上的某个节点，使某个或某些节点的左右子树的高的差从原来的 1 变为 2，从而打破了平衡，此时就需要对树进行调整来恢复平衡。

如何调整？思路又是什么？整体思路其实就是定位到不平衡的地方，然后将这个地方变为平衡。找的话很好找，只需要在做插入或删除操作时进行同步勘查即可（每个节点信息中记录了该节点高），在插入的地方向上顺着路径去找，第一个不满足平衡性的节点就是需要调整的地方。难点在于如何将其变为平衡。

因为是二叉树，无非是那么几种情况，这里还是对所有的情况进行列举。

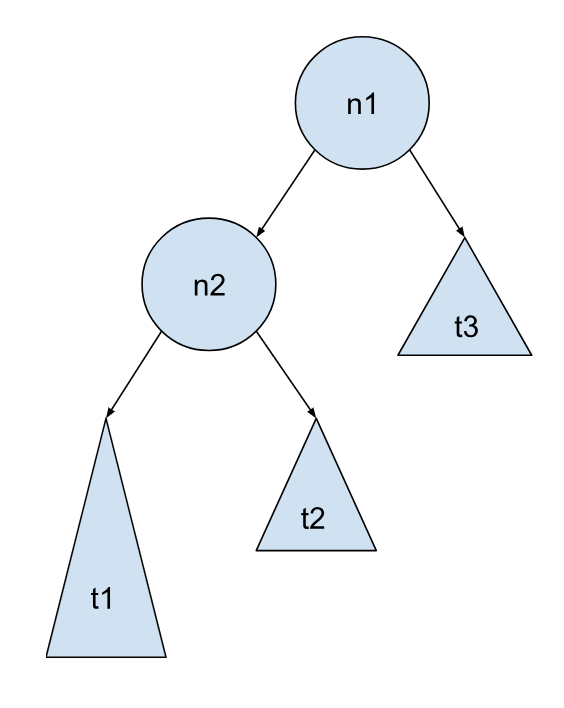
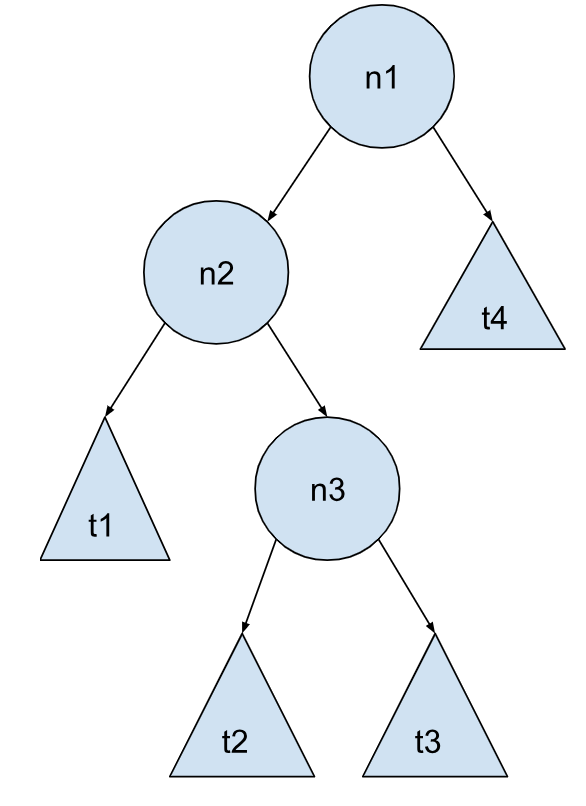
情况 1 - 插入发生在最左边的子树：

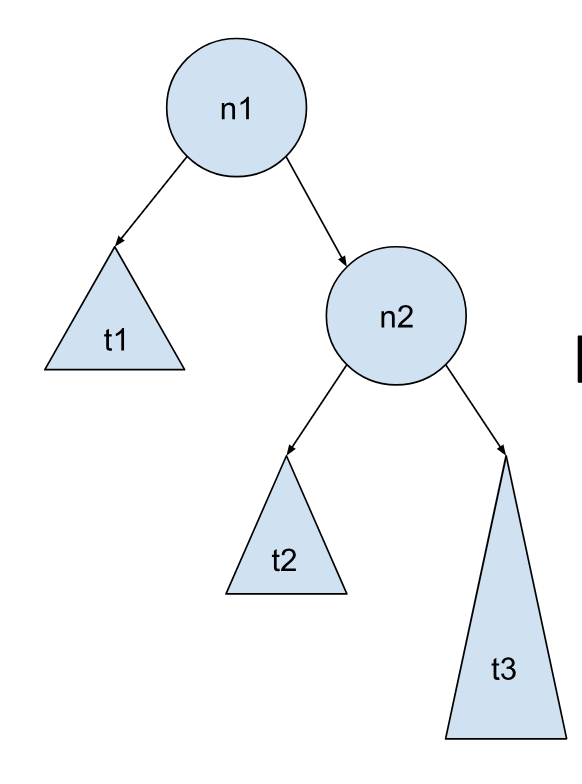
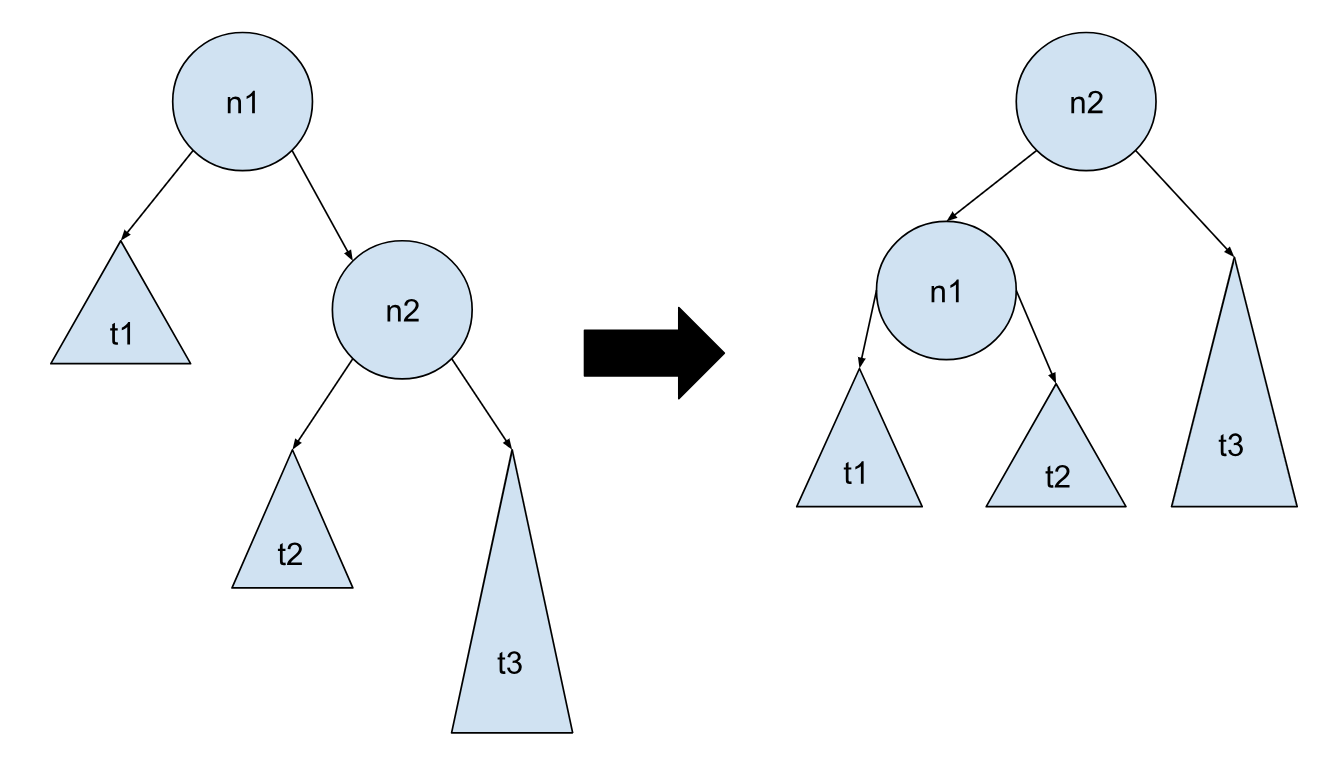
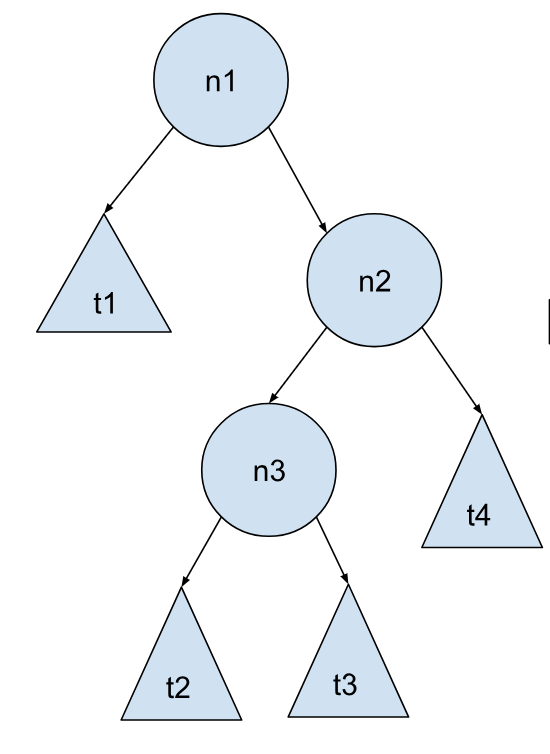
情况 2 - 插入发生在最右边的子树：

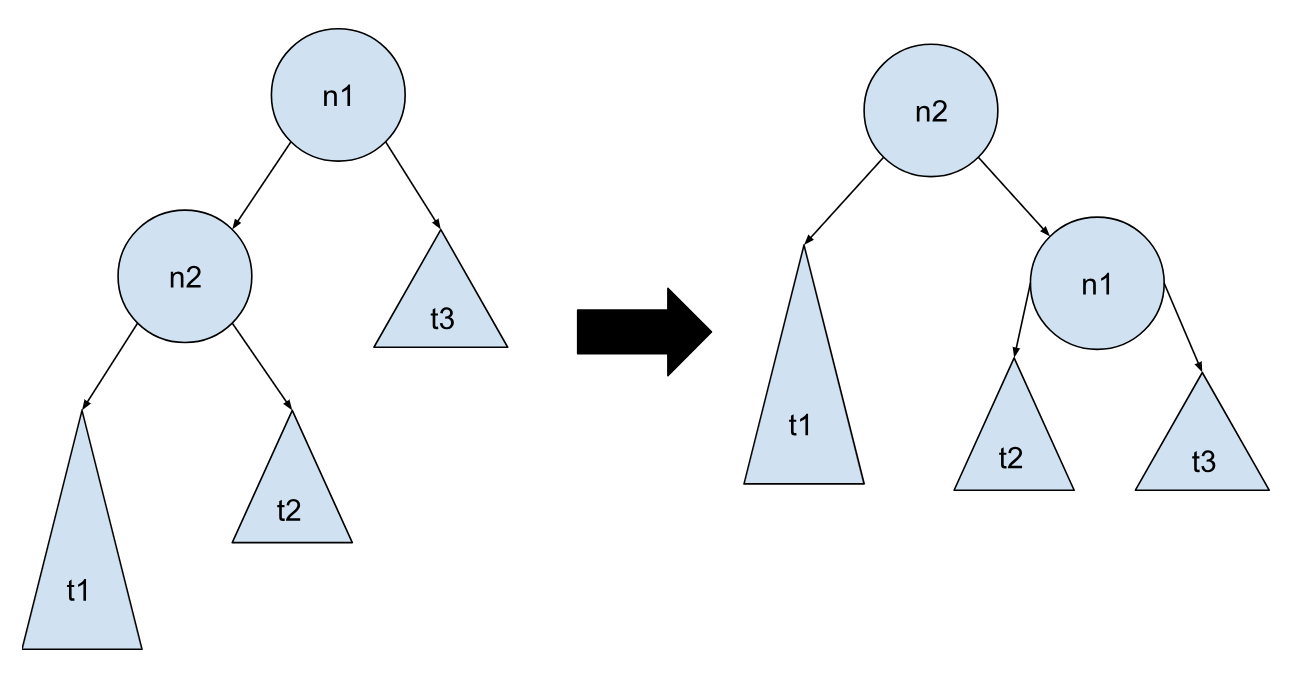
我们先来看看上面这两种情况，不平衡发生在 n1 节点处。拿情况 1 来说，这个高度差是由 t1 子树和 t3 子树造成的，需要尽量把 t1 子树上移，t3 子树下移。那具体怎么移呢？试着试着，就会发现，将 n1 节点和 n2 节点互换位置，答案便有了。在它们互换位置的同时，它们的子树也要根据二叉搜索树的定义进行相应的调整，对于情况 1 就如下图所展示的这样进行相应的变换就可以得到我们想要的结果：

情况 2 其实是情况 1 的对称情况，操作和情况 1 类似，把左右颠倒即可：

剩下还有两种情况，相比于上面的两种情况，会复杂些

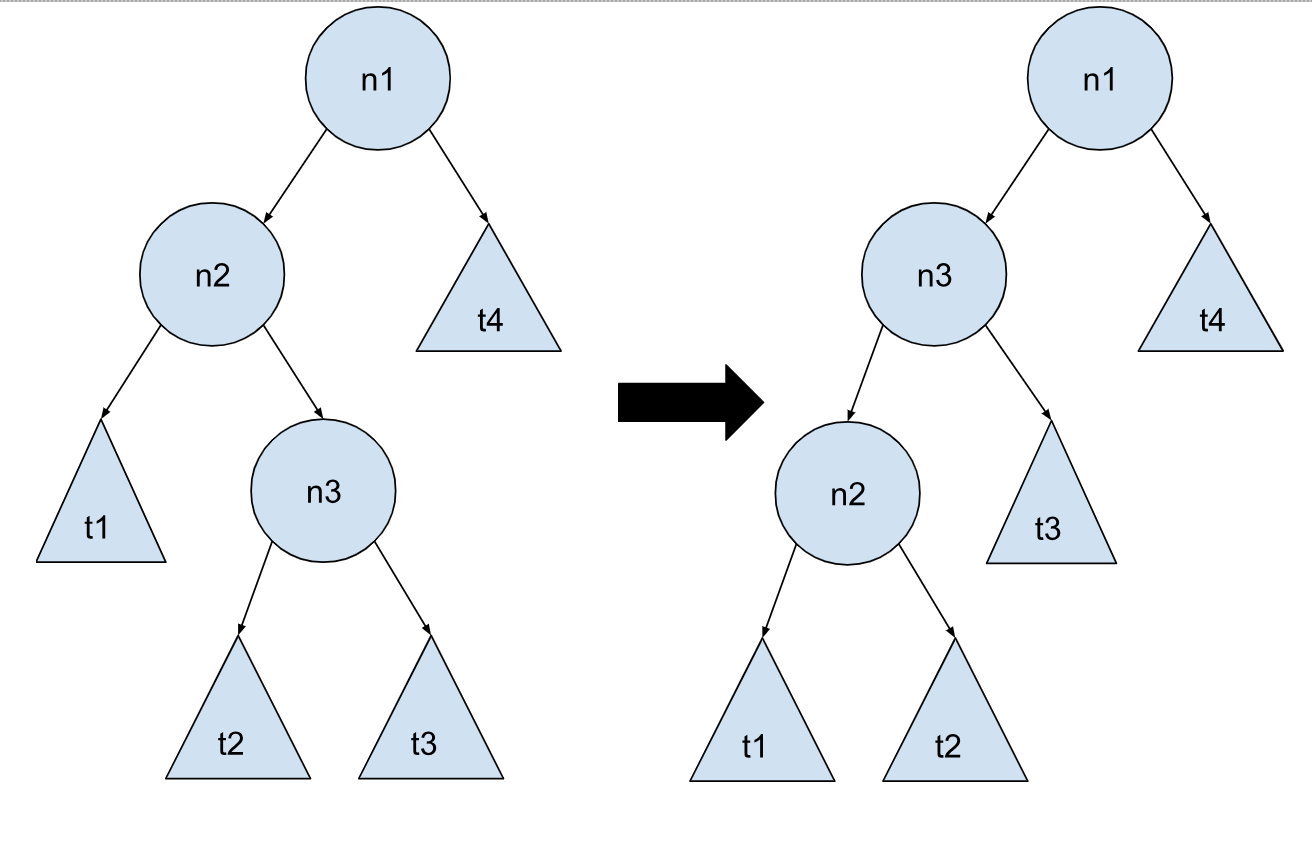
情况 3：

情况 4：

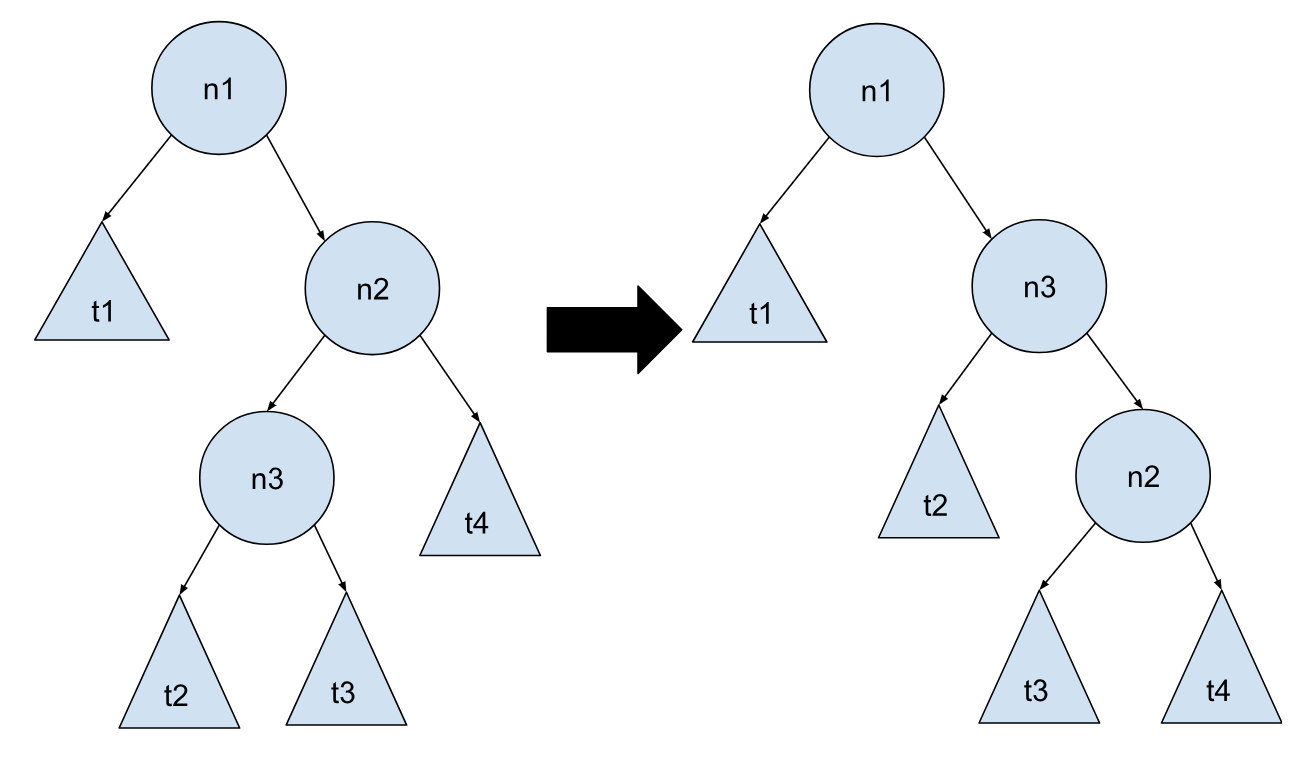
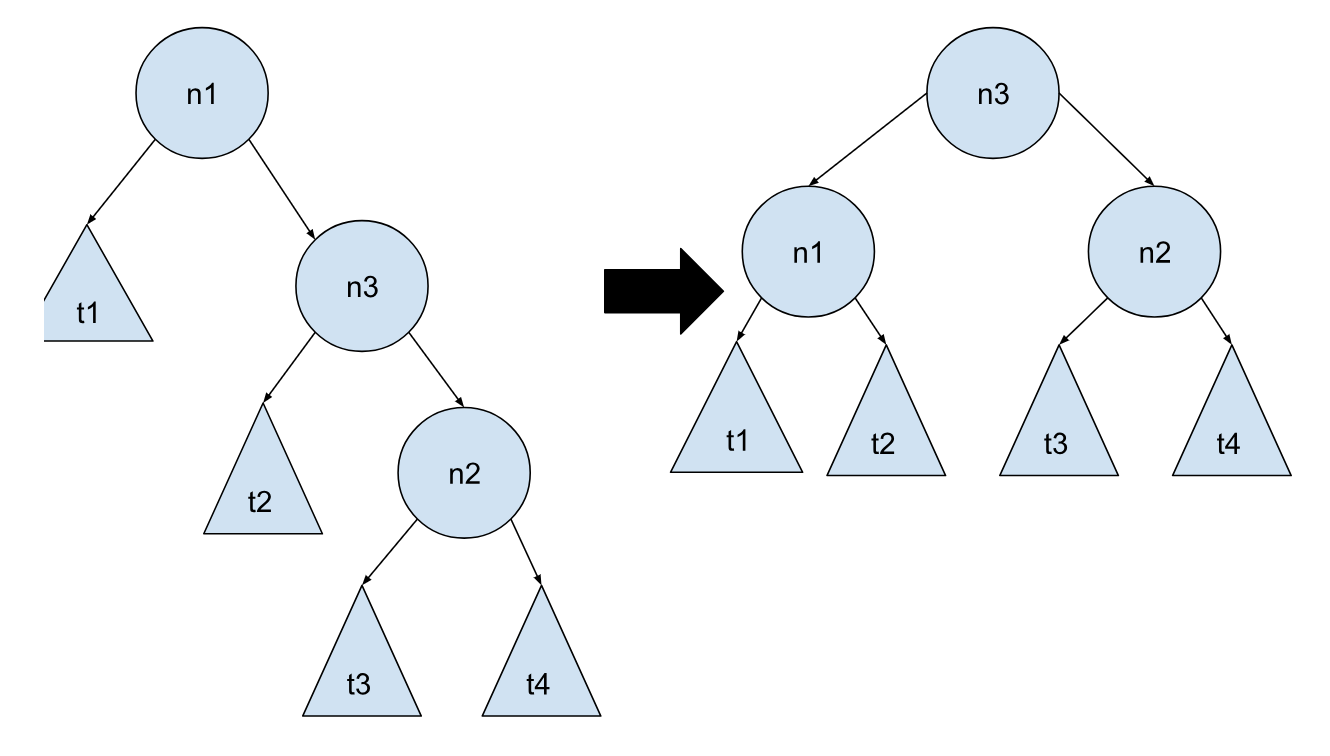
这两种情况和之前的一样，也是对称的，一种情况可以根据另一种情况如法炮制。之前的两种情况插入的点在最左边或最右边的子树，但是当插入的点在中间的时候，套用之前的方法就行不通了。为了方便展示节点的移动，这里把中间的子树画成是一个节点带两颗子树，这两颗子树我画的是一样高，但是他们按道理来说可以不一样高的，也可以是空的，但这都不是重点，重点是不平衡发生了，就拿情况 3 来举例，要尽量把 n3 所代表的子树往上移，把 t4 子树往下移。之所以会比前两个情况复杂，是因为现在有 3 个节点要考虑，但思路还是交换节点，这里我们想要尽量把 n3 往上移，最好是移到 n1 的位置。之前的例子中的交换是在父子之间进行的，那么这里有没有一种可能，我们进行两次交换，子节点先和父节点交换，然后再和祖父节点进行交换。尝试下来，最后的结果就是我们想要的：

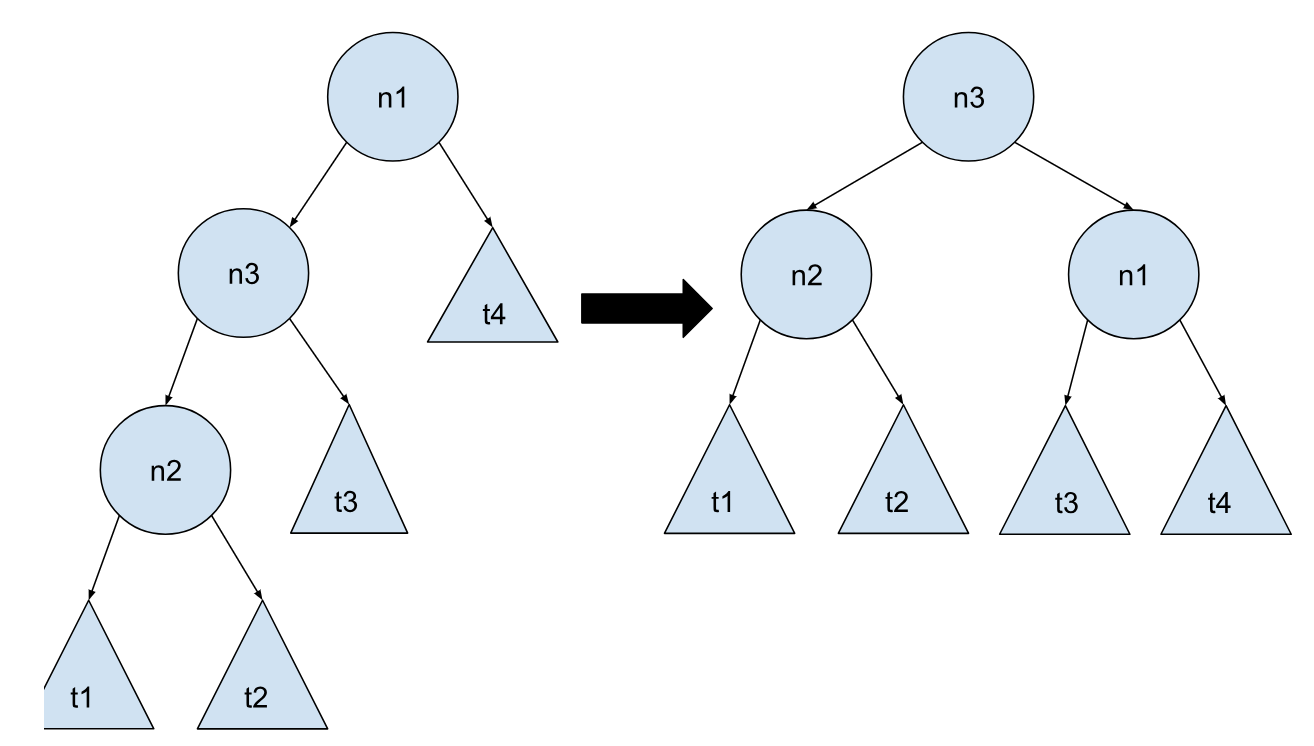
对于情况 3 来说，我们先进行一次交换，使 n3 和 n2 的位置发生交换，这一步做完，你再想想，这个是不是就是情况 1？

接着我们再让 n3 和 n1 进行位置交换

之前的 t2 t3 子树向上挪了一格，它们和 t4 子树的高度差也缩小了，我们的目的达到了。

情况 4 是和情况 3 一样的，无非是左右互换：

代码实现

我们先来看看有关平衡性调整的代码：

  
private int height(TreeNode<AnyType> t) {
  return t == null ? -1 : t.height;
}

private TreeNode<AnyType> balance(TreeNode<AnyType> t) {
  if (t == null) {
    return t;
  }

  if (height(t.left) - height(t.right) > 1) {
    if (height(t.left.left) >= height(t.left.right)) {
      // 情况 1
      t = rotateWithLeftChild(t);
    } else {
      // 情况 3
      t = doubleWithLeftChild(t);
    }
  } else if (height(t.right) - height(t.left) > 1) {
    if (height(t.right.right) >= height(t.right.left)) {
      // 情况 2
      t = rotateWithRightChild(t);
    } else {
      // 情况 4
      t = doubleWithRightChild(t);
    }
  }

  t.height = Math.max(height(t.left), height(t.right)) + 1;
  return t;
}

private TreeNode<AnyType> rotateWithLeftChild(TreeNode<AnyType> t) {
  TreeNode<AnyType> tl = t.left;
  t.left = tl.right;
  tl.right = t;
  t.height = Math.max(height(t.left), height(t.right)) + 1;
  tl.height = Math.max(height(t.left), t.height) + 1;
  return tl;
}

private TreeNode<AnyType> doubleWithLeftChild(TreeNode<AnyType> t) {
  t.left = rotateWithRightChild(t.left);
  return rotateWithLeftChild(t);
}

private TreeNode<AnyType> rotateWithRightChild(TreeNode<AnyType> t) {
  TreeNode<AnyType> tr = t.right;
  t.right = tr.left;
  tr.left = t;
  t.height = Math.max(height(t.right), height(t.left)) + 1;
  tr.height = Math.max(height(t.right), t.height) + 1;
  return tr;
}

private TreeNode<AnyType> doubleWithRightChild(TreeNode<AnyType> t) {
  t.right = rotateWithLeftChild(t.right);
  return rotateWithRightChild(t);
}

只需要对照之前的图进行条件判断，然后相对应地交换子树位置即可，这里就不过多赘述。现在的问题是，光有平衡性的调整还不够啊，还必须和二叉搜索树的插入和删除操作结合起来，毕竟还需要借助插入和删除来找到需要进行平衡性调整的子树。我们可以把之前二叉搜索树的插入和删除的代码照搬过来，然后我们在这两个操作的最后加上平衡性调整即可，完整代码如下：

  
public class AVLTree<AnyType extends Comparable<? super AnyType>> {
  private static class TreeNode<AnyType> {
    TreeNode<AnyType> left;
    TreeNode<AnyType> right;
    int height;
    AnyType val;
    TreeNode(AnyType val) {
      this(val, null, null);
    }
    TreeNode(AnyType val, TreeNode<AnyType> left, TreeNode<AnyType> right) {
      this.val = val;
      this.left = left;
      this.right = right;
      this.height = 0;
    }
  }

  private int height(TreeNode<AnyType> t) {
    return t == null ? -1 : t.height;
  }

  private static final int ALLOWED_IMBALANCE = 1;

  private TreeNode<AnyType> insert(AnyType x, TreeNode<AnyType> t) {
    if (t == null) {
      return new TreeNode<>(x, null, null);
    }

    int compareResult = x.compareTo(t.val);

    if (compareResult < 0) {
      t.left = insert(x, t.left);
    } else if (compareResult > 0) {
      t.right = insert(x, t.right);
    }

    return balance(t);
  }

  private TreeNode<AnyType> remove(AnyType x, TreeNode<AnyType> t) {
    if (t == null) {
      return t;
    }

    int compareResult = x.compareTo(t.val);

    if (compareResult < 0) {
      t.left = remove(x, t.left);
    } else if (compareResult > 0) {
      t.right = remove(x, t.right);
    } else if (t.left != null && t.right != null) {
      t.val = findMin(t.right).val;
      t.right = remove(t.val, t.right);
    } else {
      t = (t.left != null) ? t.left : t.right;
    }

    return balance(t);
  }

  private TreeNode<AnyType> balance(TreeNode<AnyType> t) {
    if (t == null) {
      return t;
    }

    if (height(t.left) - height(t.right) > ALLOWED_IMBALANCE) {
      if (height(t.left.left) >= height(t.left.right)) {
        // 情况 1
        t = rotateWithLeftChild(t);
      } else {
        // 情况 3
        t = doubleWithLeftChild(t);
      }
    } else if (height(t.right) - height(t.left) > ALLOWED_IMBALANCE) {
      if (height(t.right.right) >= height(t.right.left)) {
        // 情况 2
        t = rotateWithRightChild(t);
      } else {
        // 情况 4
        t = doubleWithRightChild(t);
      }
    }

    t.height = Math.max(height(t.left), height(t.right)) + 1;
    return t;
  }

  private TreeNode<AnyType> rotateWithLeftChild(TreeNode<AnyType> t) {
    TreeNode<AnyType> tl = t.left;
    t.left = tl.right;
    tl.right = t;
    t.height = Math.max(height(t.left), height(t.right)) + 1;
    tl.height = Math.max(height(t.left), t.height) + 1;
    return tl;
  }

  private TreeNode<AnyType> doubleWithLeftChild(TreeNode<AnyType> t) {
    t.left = rotateWithRightChild(t.left);
    return rotateWithLeftChild(t);
  }

  private TreeNode<AnyType> rotateWithRightChild(TreeNode<AnyType> t) {
    TreeNode<AnyType> tr = t.right;
    t.right = tr.left;
    tr.left = t;
    t.height = Math.max(height(t.right), height(t.left)) + 1;
    tr.height = Math.max(height(t.right), t.height) + 1;
    return tr;
  }

  private TreeNode<AnyType> doubleWithRightChild(TreeNode<AnyType> t) {
    t.right = rotateWithLeftChild(t.right);
    return rotateWithRightChild(t);
  }

  private TreeNode<AnyType> findMin(TreeNode<AnyType> t) {
    if (t == null) {
      return null;
    } else if (t.left == null) {
      return t;
    }
    return findMin(t.left);
  }

  // 测试用，可忽略
  public static void main(String[] args) {
    AVLTree<Integer> avl = new AVLTree();
    TreeNode root = new TreeNode(2, null, null);
    root.left = new TreeNode(1, null, null);
    root.right = new TreeNode(3, null, null);

    root = avl.insert(4, root);
    root = avl.insert(5, root);
    root = avl.insert(6, root);
    root = avl.insert(7, root);
    root = avl.insert(15, root);
    root = avl.insert(16, root);
    root = avl.insert(14, root);
    root = avl.insert(13, root);
    root = avl.insert(12, root);
    root = avl.insert(11, root);
    root = avl.insert(10, root);
    root = avl.insert(9, root);
    root = avl.insert(8, root);

    System.out.println(root.val);
    System.out.println(root.left.val);
    System.out.println(root.right.val);
  }
}

之前的文章中提到过 ↩

日志, 算法, 二叉树

算法二叉树

This post is licensed under CC BY 4.0 by the author.

AVL 树的基本定义

AVL 树的平衡性实现

代码实现

Trending Tags