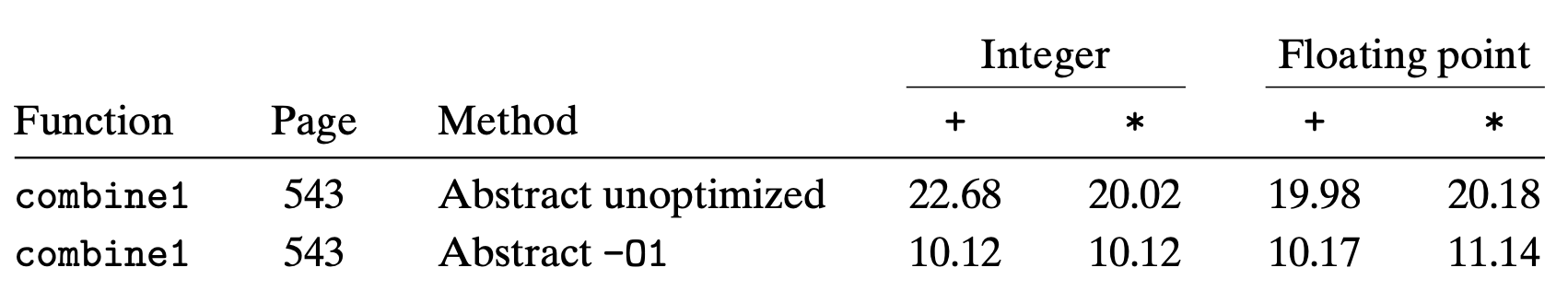运用计算机底层知识来优化程序性能
前言
这篇文章是对 CSAPP 第五章的总结回顾,所有的理论均出自该书第五章。我们前面学习了汇编指令,学习了处理器的体系结构,但是我们会发现这些东西好像离我们比较远,我们没法直接将这些知识运用到日常的编程中。那么这篇文章我们就来看看,如何运用这些底层的知识来帮助我们写出高效的程序。
编译器的瓶颈
总的说来,程序的运行效率是由下面这三个方面决定的:
- 算法和数据结构
- 编译器对源代码的优化
- 任务拆分与并行处理
这上面的第一点和第三点均不在我们的讨论范围内,我们来看看第二点。编译器会将我们写好的源码转化成机器码,也就是汇编程序,在这个转化过程中,编译器会根据我们设定的参数,对应地采取一些优化措施。这里你可能会觉得有点奇怪,优化就优化好了,为什么还需要我们设定参数?这个问题我们先放一放,来看看下面这个程序:
1
2
3
4
void twiddle1(long *xp, long *yp) {
*xp += *yp;
*xp += *yp;
}
上面这个函数执行了两次运算,按道理来说下面这个简化的函数也可得到相同的结果:
1
2
3
void twiddle2(long *xp, long *yp) {
*xp += 2* *yp;
}
但是这里我们还需要考虑一个问题,xp 和 yp 是否指向的是同一个地址,如果是同一个地址的话,假设 *xp == *yp == x,那么 twiddle1 算出来就是 4x,而 twiddle2 算出来是 3x。这种情况被称作是 memory aliasing,编译器没法对这种情况做优化。
我们再来看下面这个 C 函数:
1
2
3
4
5
6
7
8
/* Result of inlining f in func1 */
long func1in() {
long t = counter++; /* +0 */
t += counter++; /* +1 */
t += counter++; /* +2 */
t += counter++; /* +3 */
return t;
}
同样的,上面的函数可以被简化成下面这样:
1
2
3
4
5
6
/* Optimization of inlined code */
long func1opt() {
long t = 4 * counter + 6;
counter += 4;
return t;
}
因为优化过后的 C 程序更短,相对应地汇编程序也更短,指令更少,所以运行效率也更高,而且和上一个例子不同的是,这里两个函数不存在结果不一致的情况。但是这里需要注意的是,优化后的函数改变了原来的函数的代码结构,这会导致一些功能没法正常地运作,比如说设置测试断点。这种优化方式被称为 inline subsitution,编译器默认不启动,只有当我们指定时,编译器才会考虑。
因此,编译器并不是万能的,我们需要写出编译器能够优化的代码,下面我们就来看看有哪些常见的程序优化的技巧。
程序优化
我们还是先来看一个例子,然后给予这个例子一步步优化得到最终我们希望看到的程序:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
typedef long data_t;
#define IDENT 1
#define OP *
/* Create abstract data type for vector */
typedef struct {
long len;
data_t *data;
} vec_rec, *vec_ptr;
/*
* Retrieve vector element and store at dest.
* Return 0 (out of bounds) or 1 (successful)
*/
int get_vec_element(vec_ptr v, long index, data_t *dest) {
if (index < 0 || index >= v->len)
return 0;
*dest = v->data[index];
return 1;
}
/* Return length of vector */
long vec_length(vec_ptr v) {
return v->len;
}
void combine1(vec_ptr v, data_t *dest) {
long i;
*dest = IDENT;
for (i = 0; i < vec_length(v); i++) {
data_t val;
get_vec_element(v, i, &val);
*dest = *dest OP val;
}
}
这里的重点是 combine1 函数,更进一步,重点是这个函数中的循环语句,它遍历一个数组,并对数组中的每个元素挨个做运算(具体运算依照 OP 的定义),并将计算的结果保存在 dest 中。
当我们启动编译器优化,程序的性能确实有所提升,具体可以参考下表
有两点要提醒的:
- 这里的单位是 CPE(clock cycle per element)
- 这里面的数字表示的是单次循环所消耗的处理器时钟周期,而不是整个循环,因为整个循环执行是由测试数据的大小决定的,不能用于衡量性能
可以看到,在启动了编译器优化后,程序的执行效率确实有提升,我们继续看看有没有其他可以优化的地方。因为程序中的瓶颈主要是循环,因此我们把目光主要放在优化循环上。
消除循环内的函数调用
回看之前的代码,vec_length 每次循环都会执行,但是每次执行的结果都是一样的,我们可以考虑在循环前就执行,这样可以提升效率:
1
2
3
4
5
6
7
8
9
10
11
/* Move call to vec_length out of loop */
void combine2(vec_ptr v, data_t *dest) {
long i;
long length = vec_length(v);
*dest = IDENT;
for (i = 0; i < length; i++) {
data_t val;
get_vec_element(v, i, &val);
*dest = *dest OP val;
}
}
和前面的对比如下:
这个优化技巧是 code motion,也就是把那些执行多次但是并不改变结果的计算提取出来,放在循环之前执行一次就好。从上表中来看,虽然这个提升并不明显,那是因为这个函数仅仅是返回结果,并没有做其他的运算,试想一下,如果 vec_length 是下面这个 strlen 的话:
1
2
3
4
5
6
7
8
size_t strlen(const char *s) {
long length = 0;
while (*s != '\0') {
s++;
length++;
}
return length;
}
这等于说是每次循环都要将这个字符串便利一遍,这个开销是巨大的。另外,虽说 vec_length 操作简单,但是函数调用本身就会存在栈操作,最优的选项还是在循环前就把结果存在寄存器内。
除此之外,我们还可以继续优化,将循环内的另一个函数 get_vec_element 也给提取出来:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
data_t *get_vec_start(vec_ptr v) {
return v->data;
}
/* Direct access to vector data */
void combine3(vec_ptr v, data_t *dest) {
long i;
long length = vec_length(v);
data_t *data = get_vec_start(v);
*dest = IDENT;
for (i = 0; i < length; i++) {
*dest = *dest OP data[i];
}
}
但是这个优化从结果上来看,就没有起到效果:
这并不是说这个技巧没用,而是这里面有一些其他的因素限制的原因,我们后面会回过头再来看这个问题。
移除没有必要的内存引用
汇编程序往往可以给出一些优化方向,combine3 的循环内的汇编代码如下所示:
1
2
3
4
5
6
7
8
9
# Inner loop of combine3. data_t = double, OP = *
# dest in %rbx, data+i in %rdx, data+length in %rax
.L17: # loop:
vmovsd (%rbx), %xmm0 # Read product from dest
vmulsd (%rdx), %xmm0, %xmm0 # Multiply product by data[i]
vmovsd %xmm0, (%rbx) # Store product at dest
addq $8, %rdx # Increment data+i
cmpq %rax, %rdx # Compare to data+length
jne .L17 # If !=, goto loop
可以看到的是循环最后的结果是保存在 %rdx 中,而 vmovsd (%rbx), %xmm0 和 vmovsd %xmm0, (%rbx) 两条指令执行后改变了 %rbx,这个并不影响最后的结果,这两条语句可以删除,下面是优化后的代码:
1
2
3
4
5
6
7
# Inner loop of combine4. data_t = double, OP = *
# acc in %xmm0, data+i in %rdx, data+length in %rax
.L25: # loop:
vmulsd (%rdx), %xmm0, %xmm0 # Multiply acc by data[i]
addq $8, %rdx # Increment data+i
cmpq %rax, %rdx # Compare to data+length
jne .L25 # If !=, goto loop
我们也可以写出对应的 C 代码:
1
2
3
4
5
6
7
8
9
10
11
/* Accumulate result in local variable */
void combine4(vec_ptr v, data_t *dest) {
long i;
long length = vec_length(v);
data_t *data = get_vec_start(v);
data_t acc = IDENT;
for (i = 0; i < length; i++) {
acc = acc OP data[i];
}
*dest = acc;
}
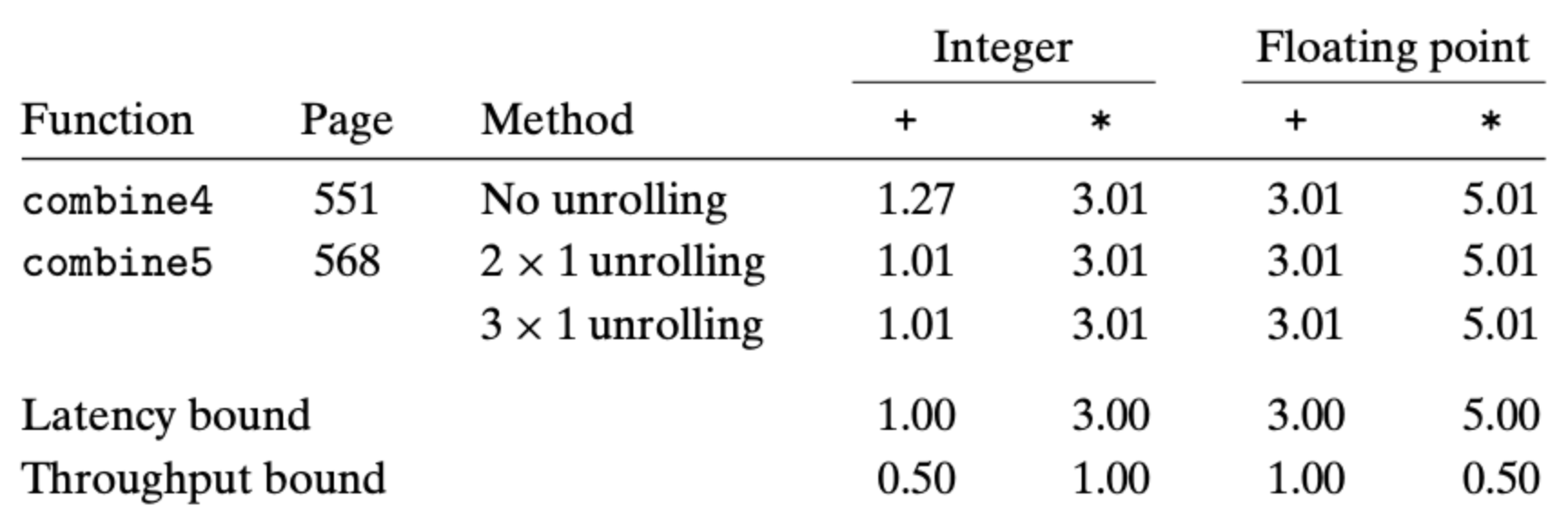
优化结果对比:
可以看到性能显著提升,之前的 combine3 每次循环都会去到内存中寻址,并将每次循环后的结果更新到这个地址上,而 combine4 中我们先将结果保存在本地变量中(寄存器),到最后循环结束才将其同步到内存中。不得不说,过多的内存操作也是循环性能低下的一个原因。
现代处理器的结构
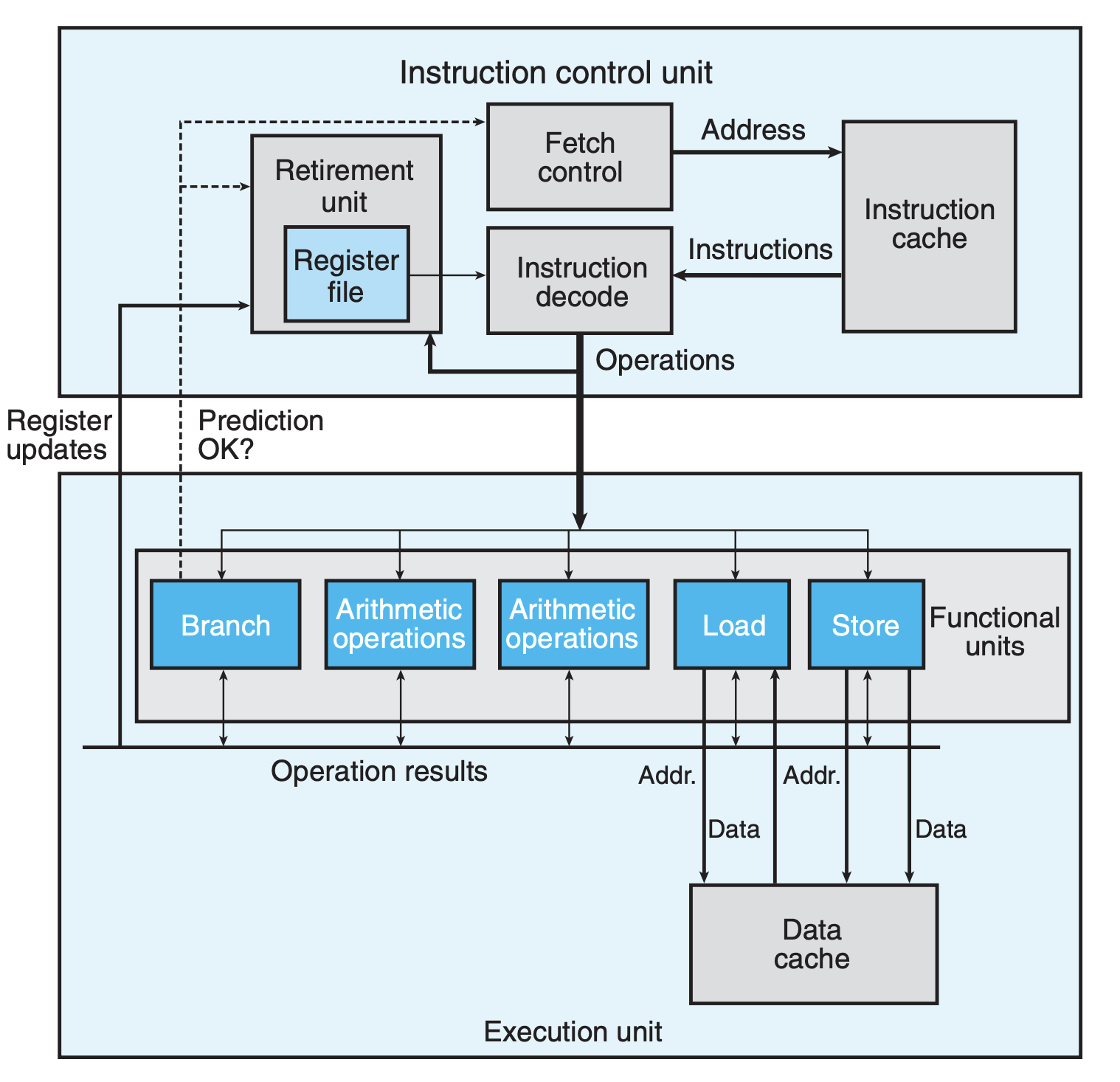
之前在 计算机处理器体系结构 我们详细地介绍了处理器的结构,这里我们再做一个简单的回顾,下图列出了现代处理器的一个大致框架:
和之前不同的是,这里我们仅仅列出了几个抽象的模块,并没有对细枝末节的东西进行展开。总体来看,有两个单元——控制单元与执行单元,控制单元决定要执行什么样的指令以及将指令发送给那个模块来执行,而执行单元主要负责执行。我们可以看到的是,像是 Arithmetic Operations 模块不止一个,多个处理单元可以为处理器并行执行提供可能。
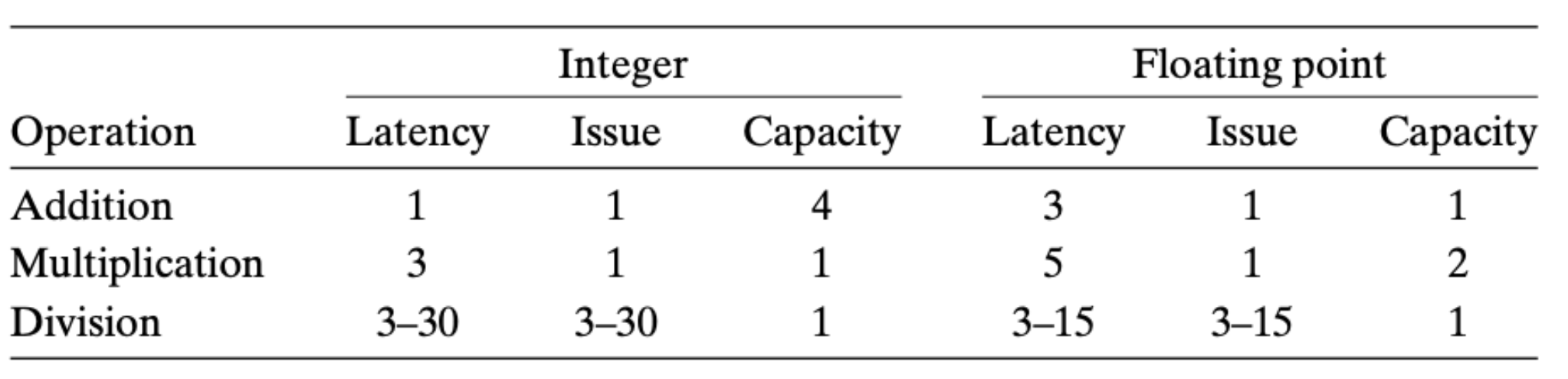
我们再来看看在这个体系下,我们如何衡量计算的性能,以 Intel i7(Haswell) 处理器为例:
这里解释下上表中出现的三个术语:
- Latency:指的是单个执行单元执行对应的算术指令所需要的时钟周期
- Issue:在单个执行单元执行时,相同类型的指令之间的最少间隔时间
- Capacity:对应的执行单元的数量
假设对于某个算术运算,I 表示的是 issue time,C 表示的是 capacity,那么我们可以得到整个处理器吞吐量为 C/I。当然了,这个不是绝对的,因为算术运算有时还会受到其他因素的影响,比如内存的 load 和 store。
知道上面这些东西有什么用呢?我们能够更清楚地知道优化的瓶颈在哪。比如对于 combine4 函数来说,从延迟(Latency)的角度来看,除了整形的加法运算,其他的类型运算已经算是最优的了:
我们还是再来看看 combine4 函数中的循环对应的汇编程序:
1
2
3
4
5
6
7
# Inner loop of combine4. data_t = double, OP = *
# acc in %xmm0, data+i in %rdx, data+length in %rax
.L25: # loop:
vmulsd (%rdx), %xmm0, %xmm0 # Multiply acc by data[i]
addq $8, %rdx # Increment data+i
cmpq %rax, %rdx # Compare to data+length
jne .L25 # If !=, goto loop
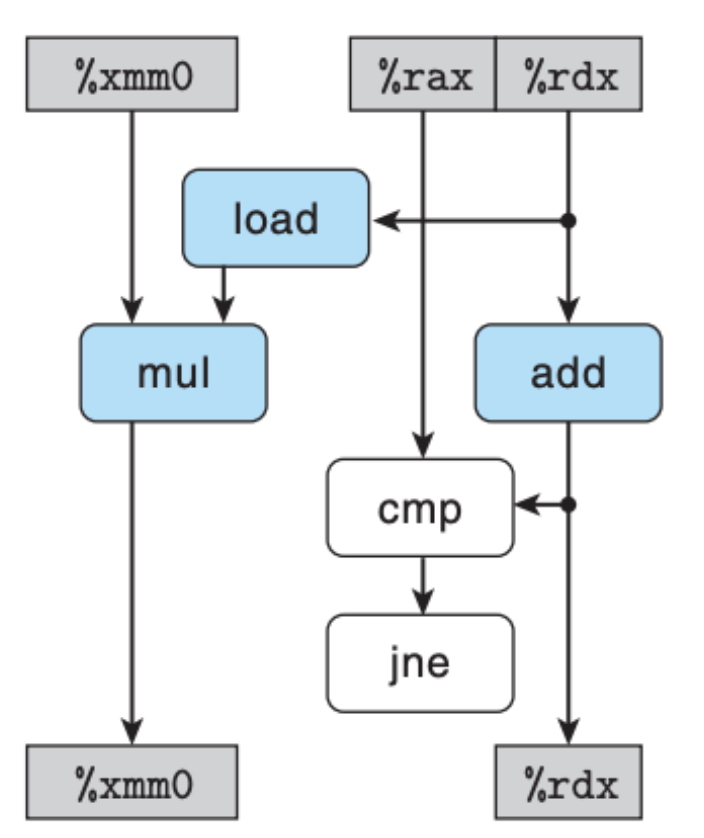
我们需要缕清的是,这里面有哪些寄存器,又有哪些操作,它们之间的关系又是什么,回答完这些问题,我们可以得到下图:
首先寄存器方面,%rax 存放的是整个数组的长度,它不会被更新,仅仅是用来比较,%rdx 可以被看作是当前数组的下标,每次循环都会更新,%xmm0 存放的是一个最终的计算累积结果,也是每次循环都会更新。
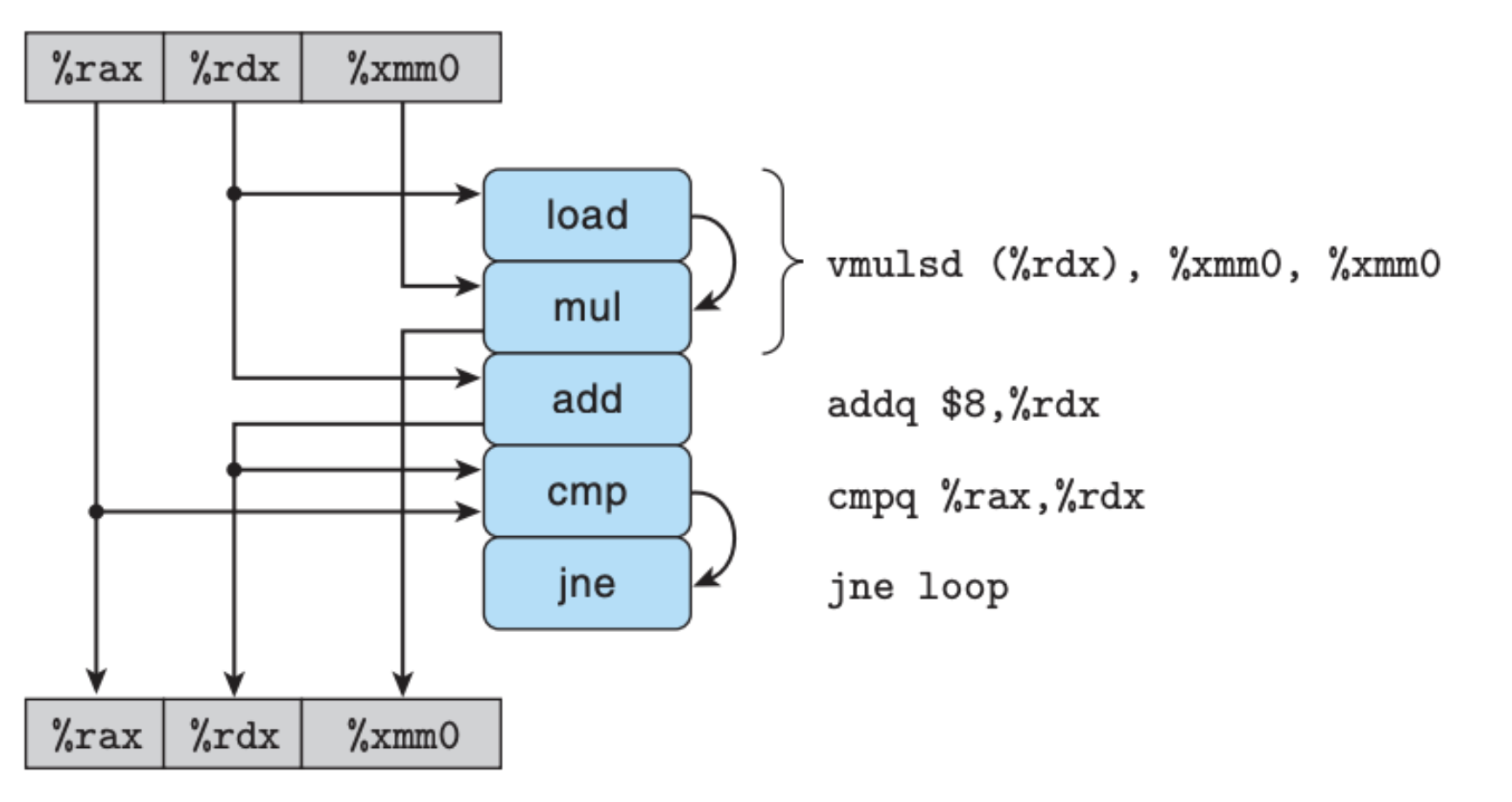
虽然说我们知道了这些信息,但是这图这么看还是比较乱,看不清依赖关系,我们将图稍作修改,就有了下面这张图:
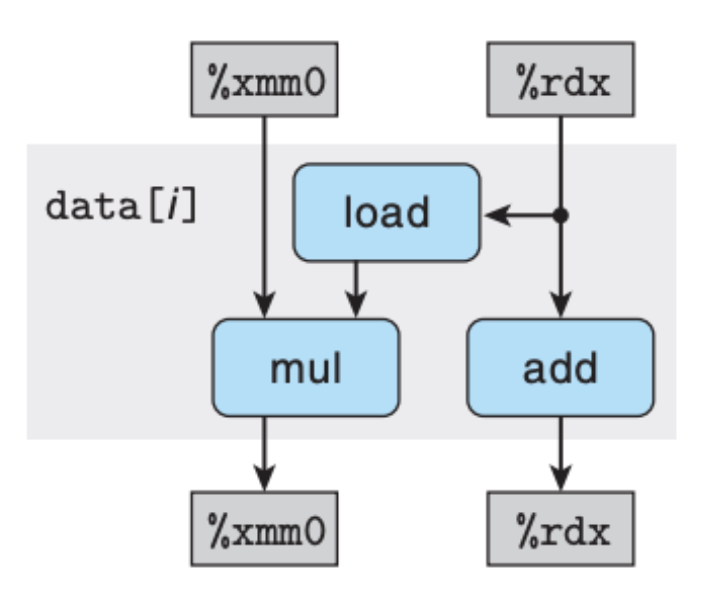
这张图中的白色方框中的操作是可以被忽略的,一个是比较操作 cmp,另一个是跳转操作 jne,这两个操作不会设计到算术运算或是操作内存,并不是影响程序性能的主要因素,这里忽略不计,于是我们还可以继续简化:
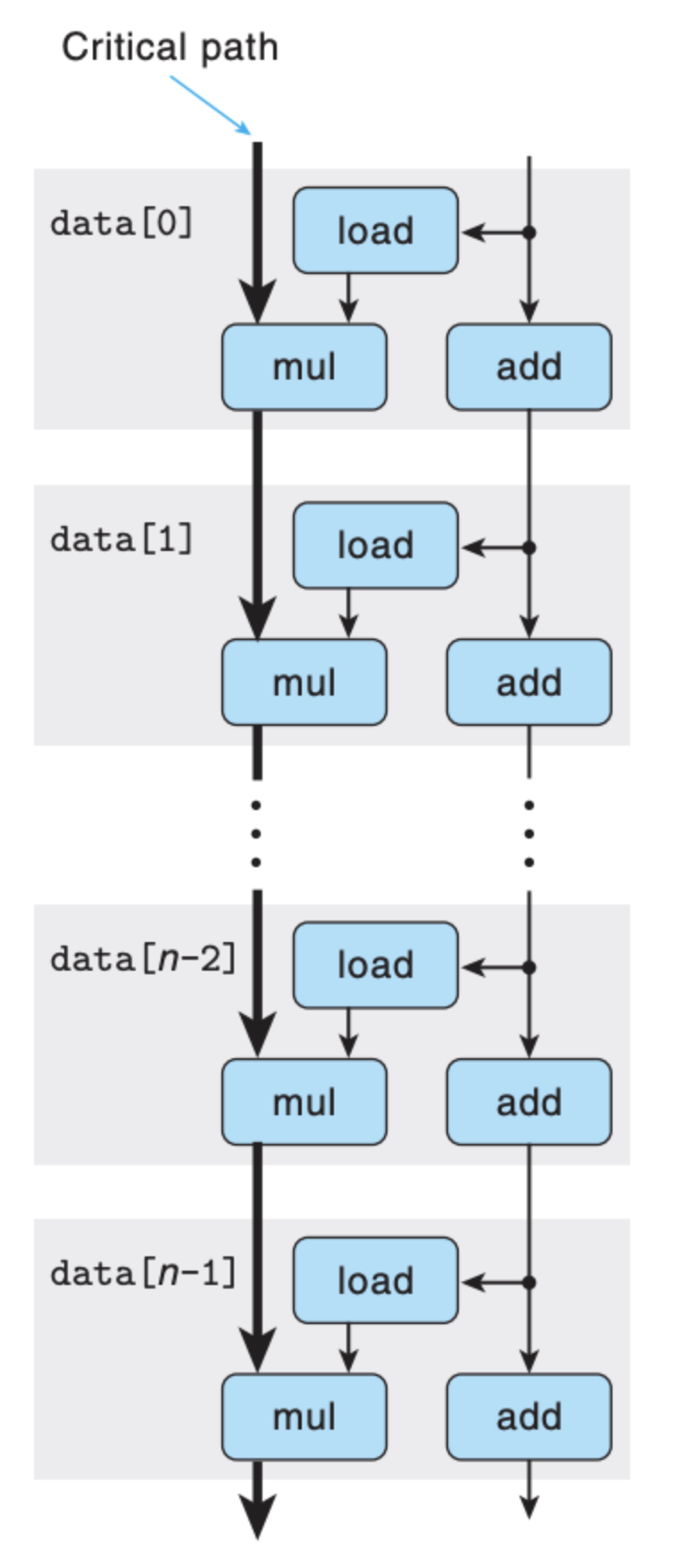
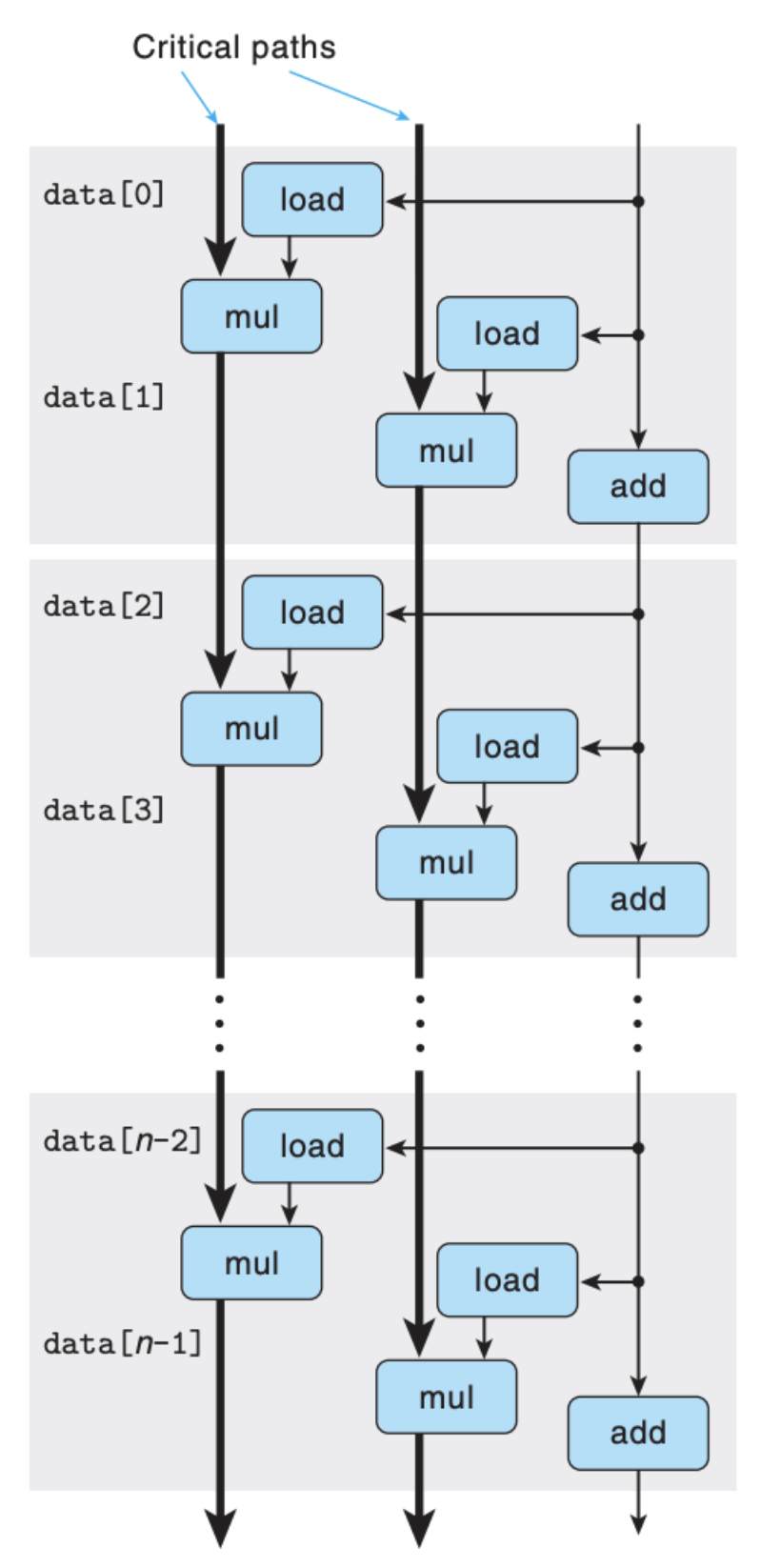
这里的依赖关系就非常明显了,并且结合每个操作所需要的时钟周期,我们可以清楚地发现 mul 操作是瓶颈,每次循环的时间是由 mul 决定的,我们还可以从整个循环来看:
当循环的次数足够多,所有的 mul 的执行时间就是整个循环的执行时间,而当 mul 执行完,load 和 add 早就执行完毕了,所以这两个操作并不决定程序运行的效率。
回到之前的问题——为什么整形的加法运算不是最优的呢? 你将依赖图中的 mul 替换成 add,相信答案是很明显的,因为这里的 add 并不构成瓶颈,整个程序的性能瓶颈是由 load+add 决定的。
循环展开(Loop Unrolling)
我们清楚了如何判定循环中的瓶颈,那么我们就可以尝试进一步去优化了,如何优化呢?还是从前面的依赖图入手,依赖图告诉我们,在每次循环中,load 操作赶不上 add 的计算,我们是否可以考虑在每次循环中多 load 几次?沿着这个思路,我们可以得到下面的 C 程序:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/* 2 x 1 loop unrolling */
void combine5(vec_ptr v, data_t *dest) {
long i;
long length = vec_length(v);
long limit = length-1;
data_t *data = get_vec_start(v);
data_t acc = IDENT;
/* Combine 2 elements at a time */
for (i = 0; i < limit; i+=2) {
acc = (acc OP data[i]) OP data[i+1];
}
/* Finish any remaining elements */
for (; i < length; i++) {
acc = acc OP data[i];
}
*dest = acc;
}
对应的汇编程序如下:
1
2
3
4
5
6
7
8
# Inner loop of combine5. data_t = double, OP = *
# i in %rdx, data %rax, limit in %rbx, acc in %xmm0
.L35: # loop:
vmulsd (%rax,%rdx,8), %xmm0, %xmm0 # Multiply acc by data[i]
vmulsd 8(%rax,%rdx,8), %xmm0, %xmm0 # Multiply acc by data[i+1]
addq $2, %rdx # Increment i by 2
cmpq %rdx, %rbp # Compare to limit:i
jg .L35 # If >, goto loop
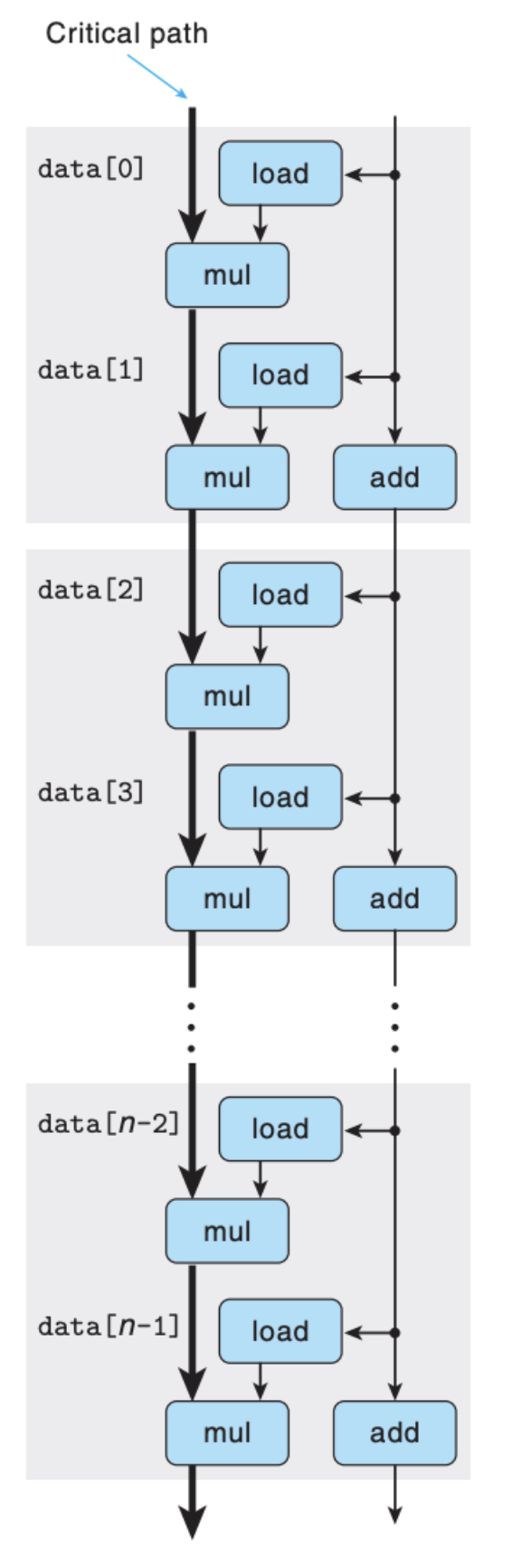
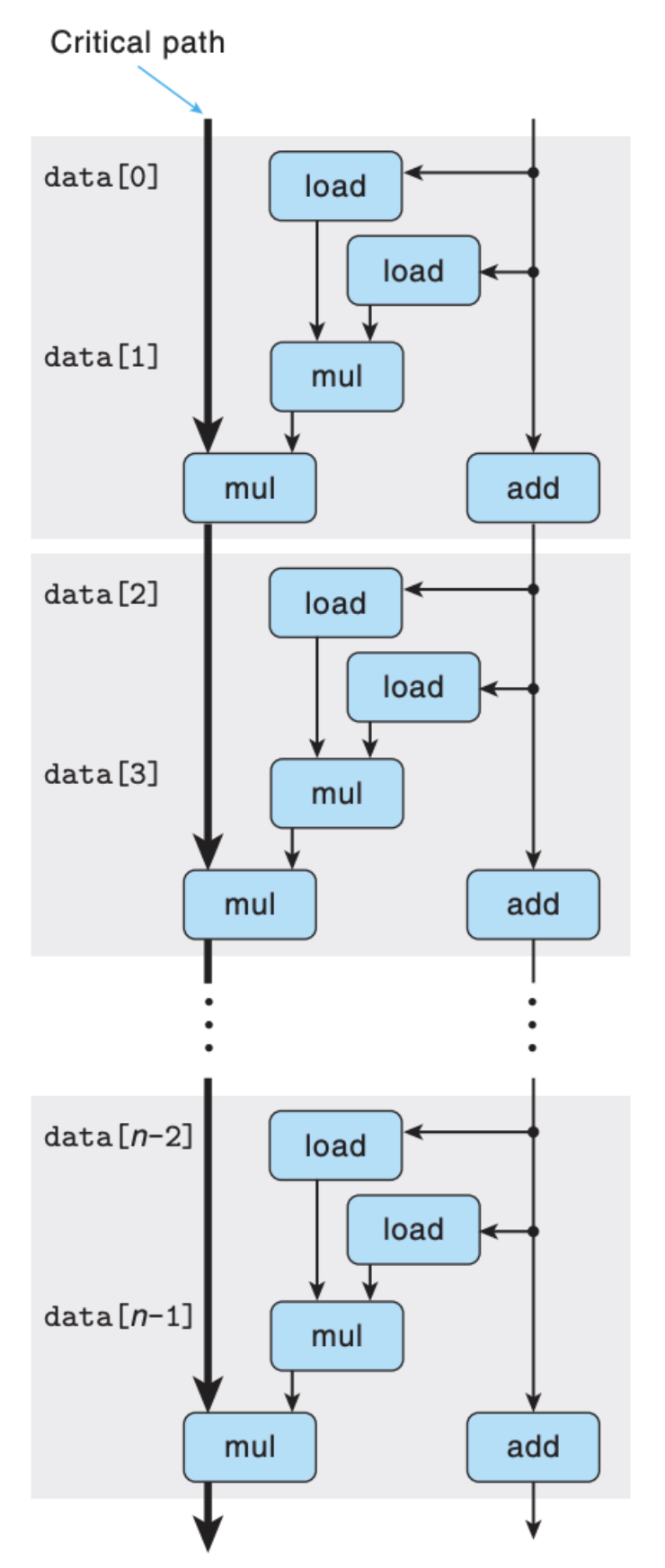
可以看到的是,在每次的循环中,我们做了两次的运算,其实整个程序做的事情总量还是一样的,只不过我们调整了依赖关系和运算的先后次序,换成依赖图就会更加清晰:
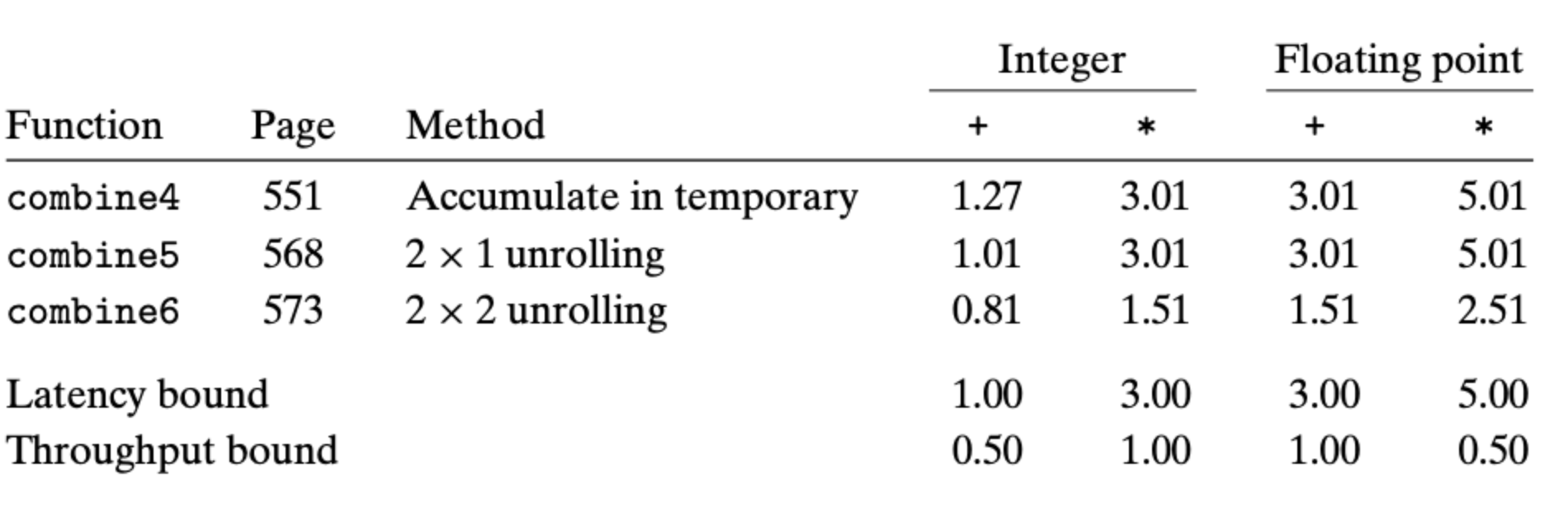
即使把图中的 mul 换成 add,瓶颈(Critical Path)依然在 add 上,这里不存在 load 不过来的情况。结果比较如下:
上表中的 2 X 1 表示的是将两次循环的合并成一次循环,也就是我们上面的代码,而 3 X 1 则是更进一步,将三次循环合并成一次循环。从表中的数据也可以看出,2 X 1 足够让我们达到最优。
多个累积变量(Multiple Accumulators)
虽然说 combine5 达到了 Latency 的瓶颈,但是从之前的架构图也可以知道,一个处理器里有多个运算单元,这里我们还需要试着增加吞吐量,让吞吐量也达到上限。于是我们可以基于 combine5 继续优化,让代码可以并行执行:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/* 2 x 2 loop unrolling */
void combine6(vec_ptr v, data_t *dest) {
long i;
long length = vec_length(v);
long limit = length-1;
data_t *data = get_vec_start(v);
data_t acc0 = IDENT;
data_t acc1 = IDENT;
/* Combine 2 elements at a time */
for (i = 0; i < limit; i+=2) {
acc0 = acc0 OP data[i];
acc1 = acc1 OP data[i+1];
}
/* Finish any remaining elements */
for (; i < length; i++) {
acc0 = acc0 OP data[i];
}
*dest = acc0 OP acc1;
}
这里我们利用了两个临时变量存放结果,并在最后将结果统一,这个方法成立的前提是运算的交换律(比如加法交换律和乘法交换律)。我们可以得到下面的表格:
同样的,我们也可以得出依赖图:
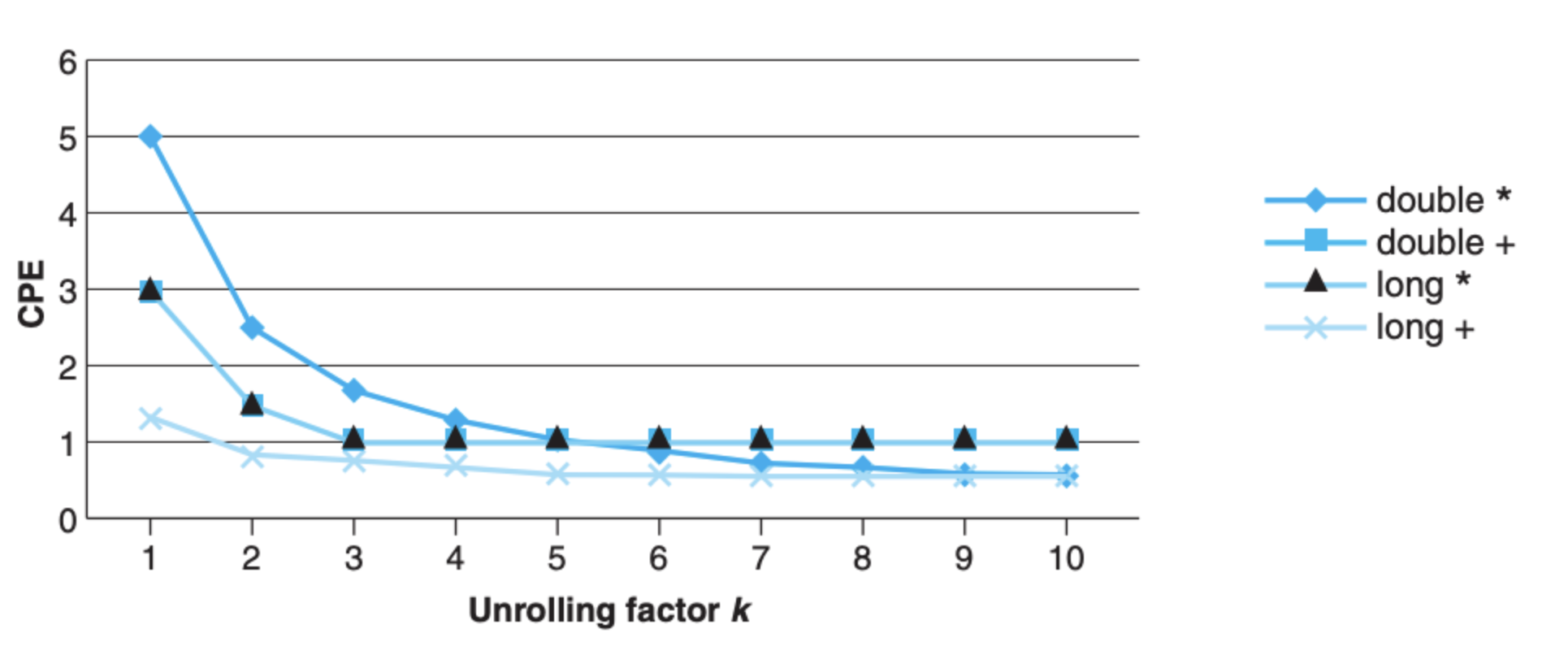
你可能会说,这也没有达到吞吐量的上限,是不是我们还有优化的空间?是的,想要增加吞吐量,就必须不间断地让执行单元执行,而上面 2 X 2 其实还不够,我们需要把这里的 2 变成 k,这个系数 k 越大,就越接近上限:
从上图中,以及结合前面的依赖图,只要能保证 k >= L * C,那么我们就可以让程序运行拥有最佳效率,但是这里也有牺牲,那就是代码的可读性。
重新结合变换(Reassociation Transformation)
上面的 combine6 是通过用多个变量来并行计算,类似的,我们也可以使用从新结合的方式来达到相同的效果:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/* 2 x 1a loop unrolling */
void combine7(vec_ptr v, data_t *dest) {
long i;
long length = vec_length(v);
long limit = length-1;
data_t *data = get_vec_start(v);
data_t acc = IDENT;
/* Combine 2 elements at a time */
for (i = 0; i < limit; i+=2) {
acc = acc OP (data[i] OP data[i+1]);
}
/* Finish any remaining elements */
for (; i < length; i++) {
acc = acc OP data[i];
}
*dest = acc;
}
你可能好奇为什么变换一下运算顺序就可以提高效率,重点在 load 操作上,可以从下面的依赖图略知一二:
上面 combine7 的运行效率和 combine6 是类似的。
优化的注意事项
寄存器的限制
过度优化可能会适得其反,比如下面这个表格显示的:
具体原因是寄存器的数量限制,在 10 X 10 下,寄存器勉强够用,所以运算可以通过下面这一条指令来完成:
1
2
# Updating of accumulator acc0 in 10 x 10 urolling
vmulsd (%rdx), %xmm0, %xmm0 # acc0 *= data[i]
而 20 X 20 的话,没有那么多的寄存器来存放临时结果,于是我们需要借助栈,这样一个运算就需要下面三个指令来完成:
1
2
3
4
# Updating of accumulator acc0 in 20 x 20 unrolling
vmovsd 40(%rsp), %xmm0
vmulsd (%rdx), %xmm0, %xmm0
vmovsd %xmm0, 40(%rsp)
这也就不难理解为什么 20 X 20 效果反而没有 10 X 10 来的好。
存取依赖
从前面的例子中,我们可以看到,很多时候我们需要从内存中加载(load)数据到处理器中,我们也需要将计算好的结果存放(store)到内存中。如果把这两个操作分开来看,事情会很简单,但是实际情况并不是这样,我们还是来看一个例子:
1
2
3
4
5
6
7
8
9
10
11
/* Write to dest, read from src */
void write_read(long *src, long *dst, long n) {
long cnt = n;
long val = 0;
while (cnt) {
*dst = val;
val = (*src)+1;
cnt--;
}
}
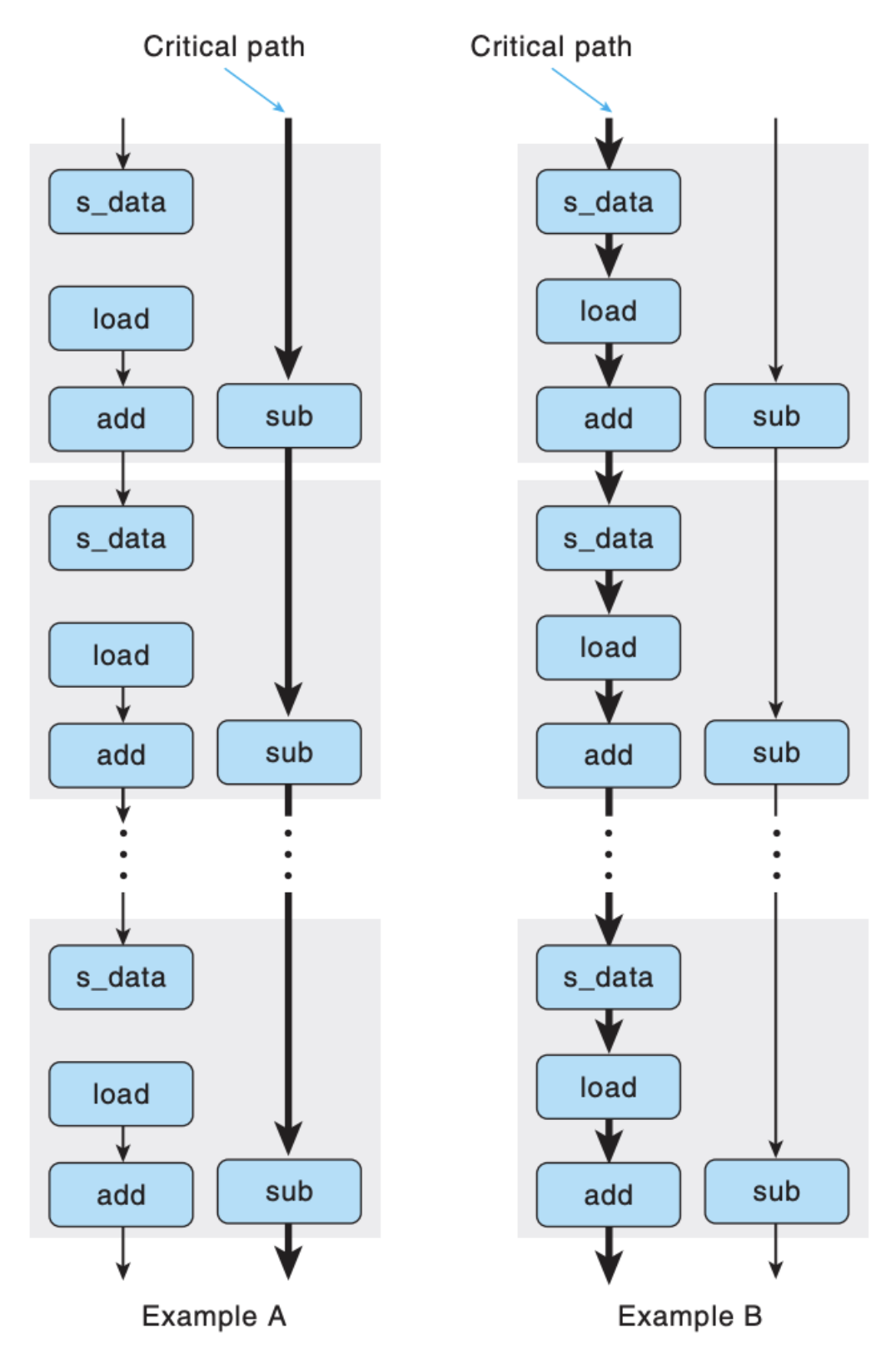
上面是一个简单的读写操作的例子,这个例子中,我们对 dst 进行写操作,对 src 进行读的操作。如果说 dst 和 src 指向的是不同的地址,那么整个程序没有任何的问题,结果也和我们设想的一样,但是如果说 dst 和 src 指向的是相同的地址,我们会得到截然不同的结果:
结果不一样是显而易见的,但是这里我们好奇的是上面两个例子的运行效率,例子 A 的 CPE 是 1.3,而例子 B 的 CPE 则是 7.3,因为例子 B 中的存取存在依赖关系。
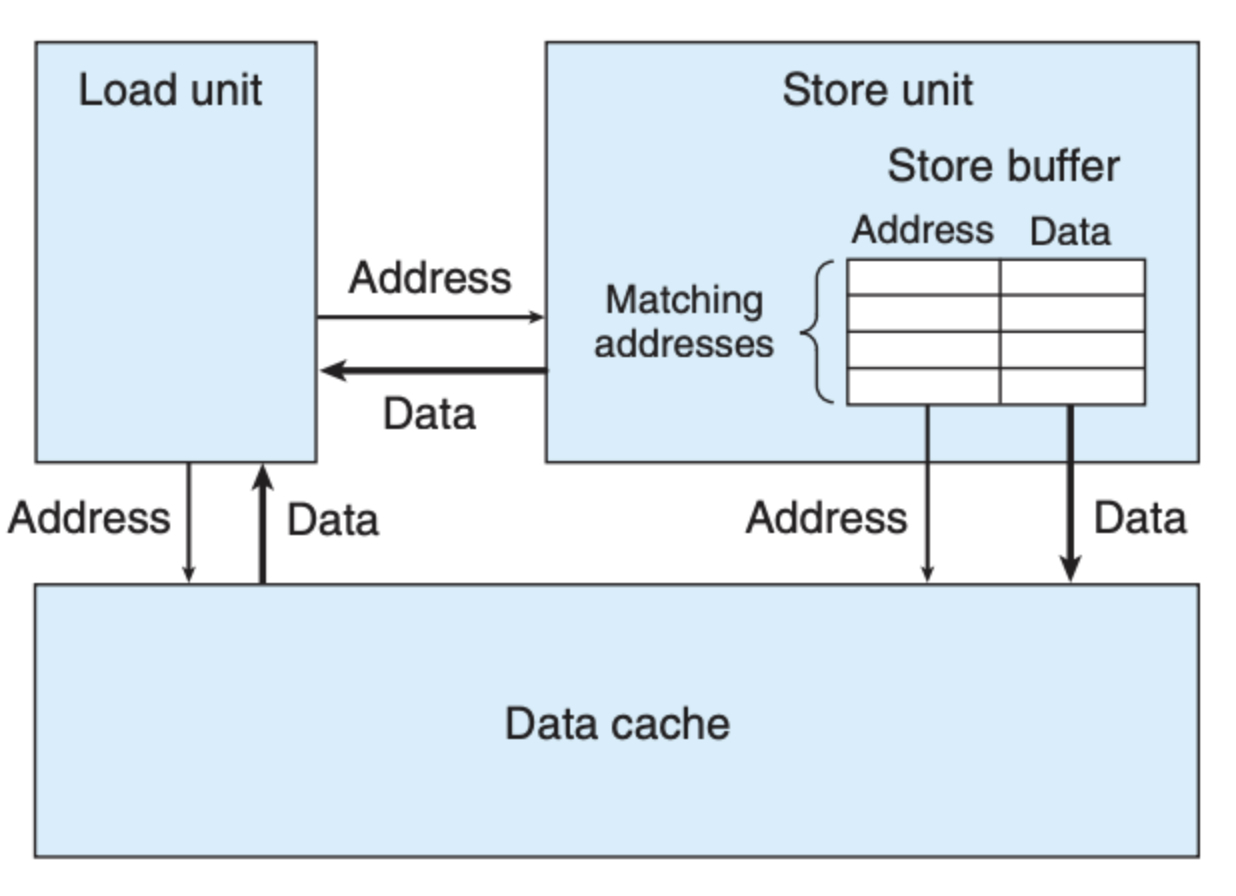
为了进一步阐述这里面的关系,我们需要了解存取单元之间的关系:
可以看到,在 store 单元内维护着一个 buffer 表,这个表中存放的是将要执行但是还未执行 store 操作的数据,功能相当于队列。每次 load 操作在执行时,需先去查看所要 load 的地址在不在 store 的 buffer 数组中,如果在的话,则需要等待地址更新后在读取。
基于此,我们也可以画出两个例子的依赖图:
两个例子的瓶颈(Critical Path)是不一样的,对于 B 来说,读写相互依赖,每一次循环的 load 操作依赖于上一次循环的 store,因而形成了瓶颈,而 A 就不存在这个问题。
条件判断
在循环里面引入条件判断会增加程序的复杂度,同时也会影响程序的运行效率。在前面的 计算机处理器体系结构 中,我们在说流水线设计的时候,我们提到条线判断靠猜,如果预测对了,那么正在流水线中执行的指令就不会被丢弃,但如果预测错了,就意味着之前的指令要被丢弃,从而影响效率。
但是这个预测是我们没有办法决定的,相比于正常的条件分支判断,更好的一种替代方式是借助条件数据移动。比如下面这个例子
1
2
3
4
5
6
7
8
9
10
11
/* Rearrange two vectors so that for each i, b[i] >= a[i] */
void minmax1(long a[], long b[], long n) {
long i;
for (i = 0; i < n; i++) {
if (a[i] > b[i]) {
long t = a[i];
a[i] = b[i];
b[i] = t;
}
}
}
毫无疑问,我们在循环中使用的条件分支,循环的 CPE 是 13.5,但是我们可以将其改写成下面这样:
1
2
3
4
5
6
7
8
9
10
/* Rearrange two vectors so that for each i, b[i] >= a[i] */
void minmax2(long a[], long b[], long n) {
long i;
for (i = 0; i < n; i++) {
long min = a[i] < b[i] ? a[i] : b[i];
long max = a[i] < b[i] ? b[i] : a[i];
a[i] = min;
b[i] = max;
}
}
上面的函数干的事情和前面的 minmax1 是一样的,但是它的循环的 CPE 是 4.0,大大优于前者。最起原因就是这里我们并没有使用分支判断,我们借助的仅仅是条件移动指令。
总结
总的来说,程序的优化可以从下面 2 个方面入手
- 遵循基本的编码原则,比如不在循环中调用函数,减少循环中的内存引用
- 借助一些底层的优化技巧,比如我们前面讲的循环展开,创建多个累积变量,将分支条件判断转化为条件移动指令等等
当然了,选择合适的算法和数据结构也是重中之重。在做优化的时候,我们可以借助一些 profiling 工具,这些工具可以帮助我们发现一个复杂的程序的瓶颈在哪,我们需要从开销大,对性能影响显著的地方入手,这样优化才会事半功倍。