计算机的机器级指令
学习汇编的意义
在说这部分内容前,先讨论一个问题,就是在当今新技术成出不穷,编程变得越来越便捷的大前提下,我们还有没有必要抽出时间来学习汇编呢?显然,如果答案是否定的,我就没必要写这篇文章了。有人会说,现在 C++ 这种语言都被归为系统级语言了,不常用了,你还学汇编,搞笑呢吧?
确实,越底层的东西越来越不适合拿来进行快节奏的开发,这其实是好事,因为编程的门槛变低了,这会让更多的人参与到编程中来。可当你把编程作为一个兴趣爱好时,你会觉得业务代码写久了也没啥意思。学习计算机专业应该是学习并理解计算机,可好像我们每天做的事情就是打开电脑,写写程序,计算机仅仅是运行我们写的东西,产生我们想要的结果,说白了,我们其实和上网炒股、看剧、买菜的大爷大妈没啥区别,他们用计算机娱乐,我们用计算机工作,二者都不了解计算机。
那怎么才算是了解计算机呢?我觉得至少得清楚它的工作原理,比如它是如何操作数据的?如何计算?如何管理内存?又是如何处理错误的?就好像一句简单的 print('Hello World!') 的背后,是计算机执行了成百上千条指令才显示在你面前的,你难道一点都不好奇这是怎么实现的吗?
要更进一步去了解计算机,汇编是少不了的,汇编说白了就是机器码,等同于二进制流,只不过为了易读,把一些指令码显示成了文本形式。相比于高级语言,汇编能够揭示很多计算机硬件相关的部件,比如寄存器、程序指针、程序栈、虚拟内存地址等等。当你了解了汇编,你其实还可以发现平时的编程中存在的问题。逆向工程(Reverse Engineering) 告诉我们,在软件开发中,可以从计算机最终产生的 0,1 二进制流,也就是这些汇编指令入手,倒推整个计算机的运行与设计原理。这其实也是学习并理解计算机最有效的途径。
话不多说,我们直接进入主题。
程序编译的几个阶段
当我们使用 gcc 来对一个 C 或 C++ 程序进行编译,到最终产生可执行的文件,这中间其实有下面几个阶段:
- 阶段一:预处理,处理文件中的外部引用(
#include)或是宏定义(#define),让源码把这部分的信息也囊括进来 - 阶段二:编译,将阶段一中产生的源码编译为汇编指令,并添加辅助信息,方便后续阶段执行
- 阶段三:产生二进制流,汇编器会依照阶段二中产生的汇编指令产生二进制流
- 阶段四:链接,最后一个阶段,将不同的二进制流文件组合起来,生成可执行文件
举个例子,有下面这段 C 程序,存储在文件 mstore.c 中
1
2
3
4
5
6
7
// mstore.c
long mult2(long, long);
void multstore(long x, long y, long *dest) {
long t = mult2(x, y);
*dest = t;
}
通过执行下面 2 个的命令,我们就可以获得阶段二、三的结果:
1
2
$> gcc -Og -S mstore.c # 获得汇编文件 -> mstore.s
$> gcc -Og -c mstore.c # 获得二进制流文件 -> mstore.o
使用下面的命令,我们就可以看到与二进制流对应的汇编指令了:
1
$> objdump -d mstore.o
文件内容:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
mstore.o: file format mach-o 64-bit x86-64
Disassembly of section __TEXT,__text:
0000000000000000 <_multstore>:
0: 55 pushq %rbp
1: 48 89 e5 movq %rsp, %rbp
4: 53 pushq %rbx
5: 50 pushq %rax
6: 48 89 d3 movq %rdx, %rbx
9: e8 00 00 00 00 callq 0xe <_multstore+0xe>
e: 48 89 03 movq %rax, (%rbx)
11: 48 83 c4 08 addq $8, %rsp
15: 5b popq %rbx
16: 5d popq %rbp
17: c3 retq
可以看到,汇编其实就是二进制流,比如 addq $8, %rsp 对应到二进制流就是 48 83 c4 08,其中 48 83 是指令 addq 的编码,c4 是寄存器 %rsp 的编码,而最后的 08 就是这条指令要操作的数了,这条指令前面的 11 表示这个指令在内存中存放的地址,当然这时还不是最终的可执行文件,没有经过最后的链接,这里的地址显示的不是真实的虚拟地址。经过链接阶段,二进制流与汇编就会是下面这样的(经过链接后,除了这个片段,还会有其他的片段,比如 main 函数,以及用到的库函数等等,这里我们就暂且略过):
1
2
3
4
5
6
7
8
9
10
11
12
0000000100003f60 <_multstore>:
100003f60: 55 pushq %rbp
100003f61: 48 89 e5 movq %rsp, %rbp
100003f64: 53 pushq %rbx
100003f65: 50 pushq %rax
100003f66: 48 89 d3 movq %rdx, %rbx
100003f69: e8 e2 ff ff ff callq 0x100003f50 <_mult2>
100003f6e: 48 89 03 movq %rax, (%rbx)
100003f71: 48 83 c4 08 addq $8, %rsp
100003f75: 5b popq %rbx
100003f76: 5d popq %rbp
100003f77: c3 retq
因为处理器的不同,关于汇编,存在着不同的版本,这里我们使用的是 ATT 版本。
寄存器与数据类型
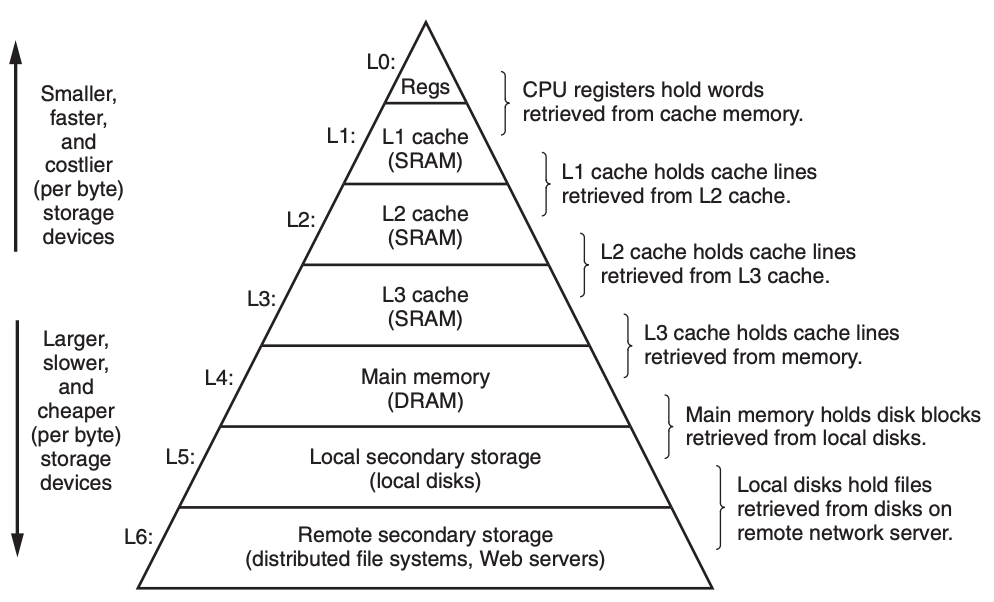
在说具体的汇编指令之前,我们有必要说一说寄存器(Register),要知道计算机的信息存储是分层的,下面这张图可以很好地反应存储层级结构:
寄存器位于图中金字塔尖,下来是一至三级缓存,然后才是内存,硬盘,最后是外部存储(也就是通过网络将信息存在其他设备,比如云存储)。金字塔越往上,存储单元的速度就越快,比如这里的寄存器就是所有存储部件中最快的,但是成本更昂贵,存储的信息就更少,所以寄存器仅仅是用来存储 CPU 当前需要马上用到的信息,并不作持久化保存。
从这张图可以衍生出 缓存(cache) 这个概念,我们平时所说的缓存并不指一个特定的存储结构,任何设备均可以当缓存,比如寄存器可以当 CPU 的缓存,内存可以当硬盘的缓存,本地硬盘又可以当其他远程设备的缓存。总的来说,高层次存储结构可以充当低层次存储结构的缓存,理解了这一点,我们就清楚在设计系统的时候,什么样的存储结构才是合理的,越高层次的存储结构应该存储越常用的信息。
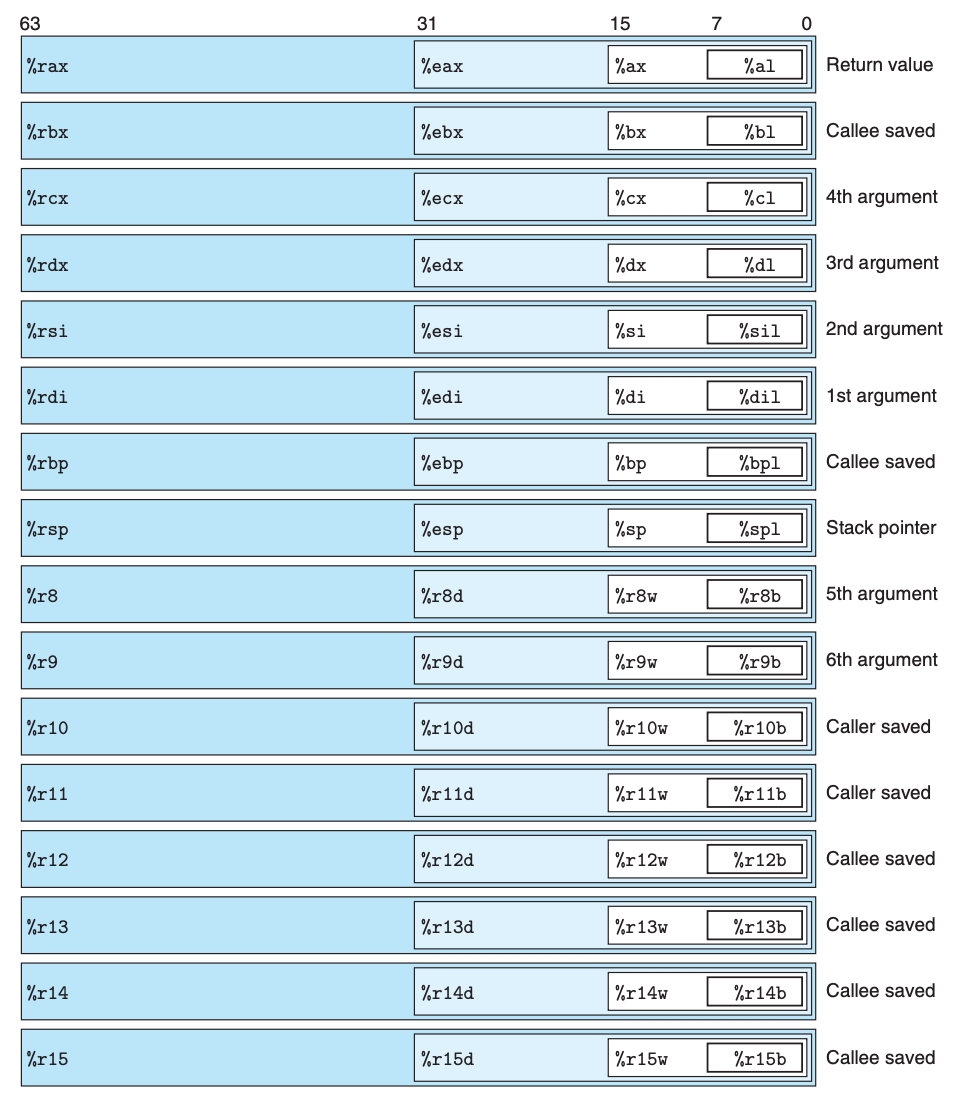
扯的有点远了,说回到寄存器,因为最早的 x86 架构是单字节的,那个时候的寄存器的存储容量就是单字节,后来慢慢演变到了 8 字节,寄存器存储的容量变大了,可是我们也需要向下兼容老版本,因此一个寄存器被拆分成不同的部分,x86-64 里有如下这些整形寄存器:
比如 %rax 寄存器是 8 字节的,%eax 可以指代它的前 32 位,%ax 可以指代它的前 16 位,%al 可以指代前 8 位。这里有一个问题,当计算机往寄存器里面写数据时,比如写进 4 字节的数据,也就是前 32 位会被使用,那另外 32 位该如何处理呢?这里有两个惯例:
- 如果写进的数据是 1 字节或者是 2 字节,那么另外的 7 字节或者 6 字节不做改变
- 如果写进的数据是 4 字节,那么另外 4 字节会被设为 0
面对不同大小的数据,汇编指令的后缀也会不同,因而同样的操作,会有多个不同的指令,下面这张表把 C 中的数据类型与汇编中的做了对照:
| C 中声明的类型 | 汇编中的类型 | 汇编指令后缀 | 大小(bytes) |
|---|---|---|---|
| char | Byte | b | 1 |
| short | Word | w | 2 |
| int | Double word | l | 4 |
| long | Double word | q | 8 |
| char * | Quad word | q | 8 |
| float | Single precision | s | 4 |
| double | Double precision | l | 8 |
类型的名称是由 Intel 公司起的,这不重要,重要的是指令的后缀,后面我们会看到一种操作有好多种版本,比如,mov 操作对应的实际指令就有 movb, movw, movl, movq,它们的功能没有区别,只不过是针对的数据类型(大小)不一样。
常见的汇编指令
寻址操作
很多时候,数据在内存中,寄存器当中存放的是内存的地址。这个时候就需要使用寻址操作,格式如下:
\[Imm(r_b,r_i,s)\]其中,
- Imm 表示的是偏移量
- $r_b$ 寄存器中存放的是基准值(base register)
- $r_i$ 寄存器中存放的是索引值(index register)
- $s$ 表示的模值(scale factor)
上式所代表的地址可以通过下面的计算得出:
\[Imm+R[r_b]+R[r_i]*s\]这看的是不是很奇怪,这都是些啥啊?一个寻址都搞的这么复杂,有必要吗?上面的式子只是一个通用的写法,为了表明所有的情况,这里面的所有的元素都可以缺省,这样的话其实就有下面这些情况:
| 类型 | 格式 | 操作值 | 名称 |
|---|---|---|---|
| Immediate | $Imm | Imm | Immediate |
| Register | $r_a$ | $R[r_a]$ | Register |
| Memory | Imm | $M[Imm]$ | Absolute |
| Memory | $(r_a)$ | $M[R[r_a]]$ | Indirect |
| Memory | $Imm(r_b)$ | $M[Imm+R[r_b]]$ | Base + Displacement |
| Memory | $(r_b,r_i)$ | $M[R[r_b]+R[r_i]]$ | Indexed |
| Memory | $Imm(r_b,r_i)$ | $M[Imm+R[r_b]+R[r_i]]$ | Indexed |
| Memory | $(,r_i,s)$ | $M[R[r_i]*s]$ | Scaled indexed |
| Memory | $Imm(,r_i,s)$ | $M[Imm+R[r_i]*s]$ | Scaled indexed |
| Memory | $(r_b,r_i,s)$ | $M[R[r_b]+R[r_i]*s]$ | Scaled indexed |
| Memory | $Imm(r_b,r_i,s)$ | $M[Imm+R[r_b]+R[r_i]*s]$ | Scaled indexed |
把这个表格多看几遍,重点在格式与操作值的对应关系上,你一定能看出规律:
- 操作符的类型就 3 种,常量,寄存器以及内存。常量在这里不表示任何意义,就是一个数,比如之前的
addq $8, %rsp中的$8就是一个常量 - 寄存器和常量的格式都只有一种,剩下的全是内存寻址
- 数字带不带 $ 来区别是常量还是内存寻址
- 寄存器带不带括号
()来区别是直接操作寄存器还是用寄存器中的数据来做内存寻址
可为什么有这么多种类的内存寻址呢?可以想想数组和指针,说的更准确些,C 语言当中的数组和指针。每当我们需要操作或者查看一个连续区域时,这些内存寻址操作就能派上用场。
数据移动指令
数据移动指令是汇编中最常见的指令,格式是 mov S,D,最终是把 S 中的数据移到 D 中,依照操作数类型的不同,有下面这些指令:
| 指令 | 描述 |
|---|---|
| movb | 移动单字节数据 |
| movw | 移动双字节数据 |
| movl | 移动四字节数据 |
| movq | 移动八字节数据 |
| movzbw | 移动单字节数据到双字节寄存器中,并将高位置 0 |
| movzbl | 移动单字节数据到四字节寄存器中,并将高位置 0 |
| movzwl | 移动双字节数据到四字节寄存器中,并将高位置 0 |
| movzbq | 移动单字节数据到八字节寄存器中,并将高位置 0 |
| movzwq | 移动双字节数据到八字节寄存器中,并将高位置 0 |
| movsbw | 移动单字节数据到双字节寄存器中,并将高位置成符号位(最高位) |
| movsbl | 移动单字节数据到四字节寄存器中,并将高位置成符号位(最高位) |
| movswl | 移动双字节数据到四字节寄存器中,并将高位置成符号位(最高位) |
| movsbq | 移动单字节数据到八字节寄存器中,并将高位置成符号位(最高位) |
| movswq | 移动双字节数据到八字节寄存器中,并将高位置成符号位(最高位) |
| movslq | 移动四字节数据到八字节寄存器中,并将高位置成符号位(最高位) |
| cltq | 效果等同于 movslq %eax, %rax,但是指令占用空间更少 |
这里面 movz 打头的指令主要针对的是无符号数,而 movs 打头的指令针对的是有符号数。之所以弄出这么多个版本,主要是为了解决两个问题:
- 操作不同大小的数据类型对寄存器的改变是不一样的
- 是否需要用大的寄存器指代小寄存器中存放的值?(比如是否需要使
%rax和%ax中的数据表示的内容一致)
说白了就是,同样的操作,但是对象不同,生成了这么多的指令。很多人可能会觉得,这不是在把简单的问题复杂化吗?计算机难道自己不能去判断操作数的类型吗?要知道,这些都是最底层的东西,计算机会根据这些指令直接改变门电路,如果这里还要计算机自己去判断,那么本来一条指令的工作,最后会增加到 4 条甚至更多,而底层操作就那么些,它们出现的频率相当高,这等于说是把一个程序的执行时间乘上了 4,属实不是我们希望的。
这里我们来看下面这个 C 程序:
1
2
3
4
5
long exchange(long *xp, long *yp) {
long x = *xp;
*xp = y;
return x;
}
上面的程序会对应生成如下的汇编指令:
1
2
3
4
exchange:
movq (%rdi), %rax
movq %rsi, (%rdi)
ret
从中我们也可以发现,C 语言的指针其实就是单纯的内存地址,按照惯例,类似函数中 x 这样的局部变量大多会优先保存在寄存器中,而不是内存中,因为这样速度更快,当然,这其实是编译器决定的。
栈操作指令
关于栈,大多数人首先想到的是它的先进先出(LIFO)的特质,可它的用途却不止这么简单,它是计算机中非常重要的一个结构,我们后面还会介绍各种栈的知识,这里只需要知道下面几点:
- x86-64 中,栈也是存放在内存中的,说的更清楚些,和数组类似,栈也是内存中的一段连续区域
%rsp寄存器中存放的是栈顶的内存地址,栈操作都会涉及到更新%rsp寄存器- 往栈中插入元素,内存地址向下递减
- 从栈中删除元素,内存地址向上递增
栈的两个操作——插入和删除,分别对应的下面两个指令:
| 指令 | 功能 | 描述 |
|---|---|---|
| pushq S | R[%rsp] <- R[%rsp]-8; M[R[%rsp]] <- S | 向栈顶插入元素 |
| popq D | D <- M[R[%rsp]]; R[%rsp] <- R[%rsp]+8 | 从栈顶移除元素 |
可以看到不管是插入还是删除,指令干了两件事,向内存中存取数据,以及更新 %rsp 寄存器。栈操作的都是 8 字节的数据,因而不存在不同类别的指令,每个操作仅对应一个指令,相比于 mov 操作,看着让人舒服了不少。
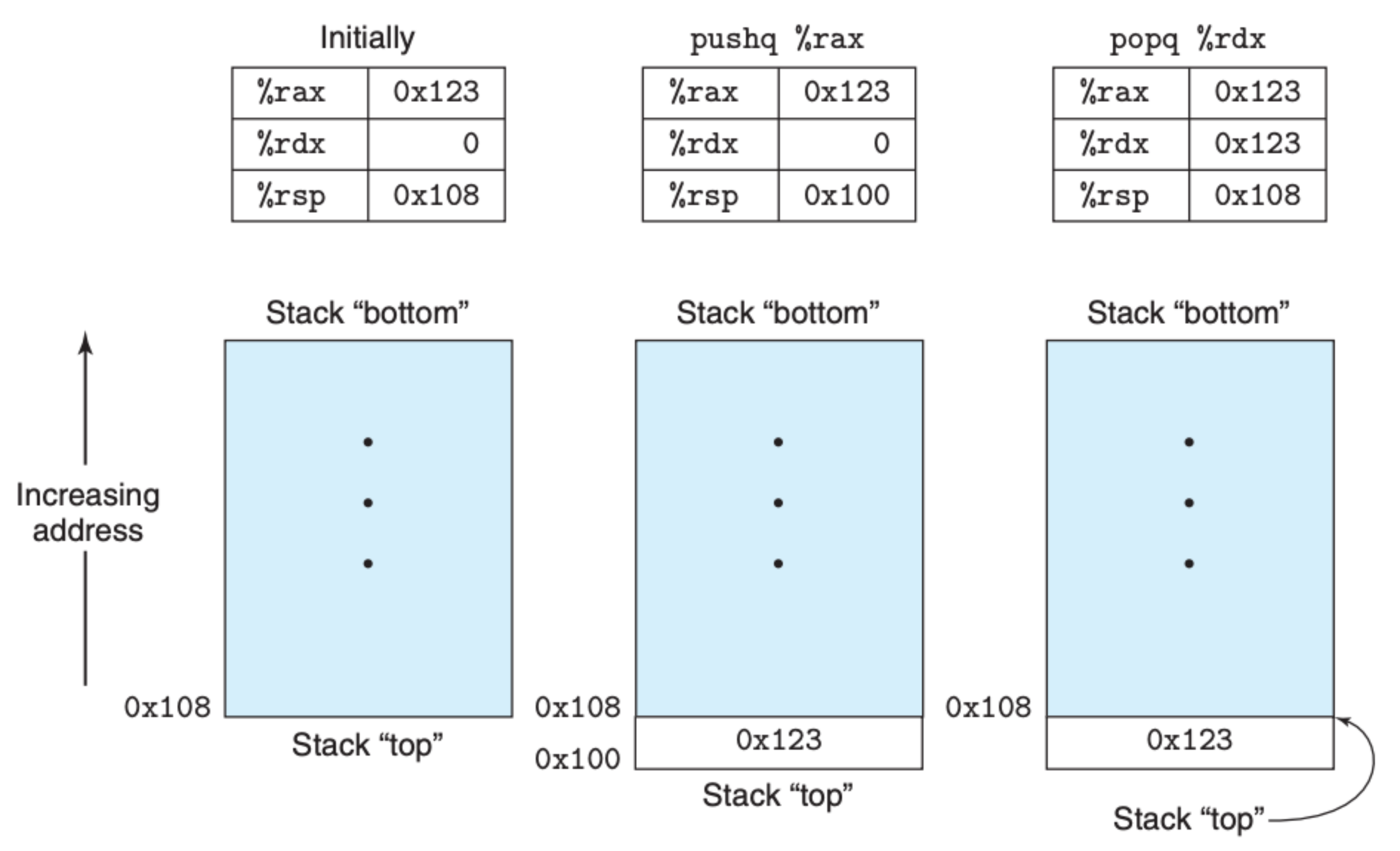
下图显示的就是栈操作的直观情况:
因为栈在内存中,所以我们也可以通过 mov 指令拿到栈中的数据,比如 movq 8(%rsp), %rdx。当然栈操作也可以写成其他的形式,比如 pushq %rbp 可以写成下面两个指令的组合:
1
2
subq $8, %rsp
movq %rbp, (%rsp)
popq %rax 可以写成:
1
2
movq (%rsp), %rax
addq $8, %rsp
是先更新 %rsp 还是先操作内存,这个顺序很重要,这个我们在说指令执行的时候会重点提到。
运算指令
x86-64 有下面这些与计算相关的指令:
| 指令 | 功能 | 描述 |
|---|---|---|
| leaq S,D | D <- &S | 存取内存地址 |
| INC D | D <- D+1 | 自增 |
| DEC D | D <- D-1 | 自减 |
| NEG D | D <- -D | 取负 |
| NOT D | D <- ~D | 取非 |
| ADD S,D | D <- D+S | 加法运算 |
| SUB S,D | D <- D-S | 减法运算 |
| IMUL S,D | D <- D*S | 乘法运算 |
| XOR S,D | D <- D^S | 异或运算 |
| OR S,D | D <- D \| S | 或运算 |
| AND S,D | D <- D&S | 与运算 |
| SAL k,D | D <- D << k | 左移 |
| SHL k,D | D <- D << k | 左移(与 SAL 一样) |
| SAR k,D | D <- D >> k | 算术右移 |
| SHR k,D | D <- D >> k | 逻辑右移 |
上面的指令中,除了 leaq 外,其余的指令都存在多个版本(类似 mov),主要看指令的后缀。
leaq 和 movq 类似,但是它仅仅是计算地址,并将其存放到寄存器中,并不会读取内存中的内容,比如下面的 C 函数:
1
2
3
4
long scale(long x, long y, long z) {
long t = x + 4 * y + 12 * z;
return t;
}
转换为汇编就是:
1
2
3
4
5
6
x in %rdi, y in %rsi, z in %rdx
scale:
leaq (%rdi,%rsi,4), %rax
leaq (%rdx,%rdx,2), %rdx
leaq (%rax,%rdx,4), %rax
ret
要知道运算指令,尤其是乘法和除法是开销很大的,leaq 指令在一定程度上提升了效率。
控制指令
程序中有很多的条件判断以及循环,这些结构的实现主要是依赖于底层的控制逻辑。CPU 中维护着下列条件码:
| 条件位 | 描述 |
|---|---|
| CF | 表示无符号操作是否溢出 |
| ZF | 表示最近的一次操作是否产生的结果为 0 |
| SF | 表示最近的一次操作是否产生了负数 |
| OF | 表示有符号操作是否溢出 |
这些条件码其实就是单个的 bit 位,用来表示当前操作的情况,前面说的运算操作的结果会改变这些条件位,还有就是下面两个操作也会改变这些条件位:
| 指令 | 功能 | 描述 |
|---|---|---|
| CMP S1,S2 | S2 - S1 | 比较两数大小,更新条件位 |
| TEST S1,S2 | S1 & S2 | 两数相与,更新条件位 |
这有什么用呢?我们的控制指令都会依照这些条件位,进行程序逻辑的控制,比如非常常见的 jump 指令:
| 指令 | 条件 | 描述 |
|---|---|---|
| jmp Label | 1 | 直接跳转 |
| jmp *Operand | 1 | 间接跳转(跳转目标从寄存器或者内存中读取) |
| je Label | ZF | 条件跳转(等于 0 时跳转) |
| jne Label | ~ZF | 条件跳转(不等于 0 时跳转) |
| js Label | SF | 条件跳转(负数时跳转) |
| jns Label | ~SF | 条件跳转(不为负数时跳转) |
| jg Label | ~(SF^OF)&~ZF | 条件跳转(有符号数大于 > 时跳转) |
| jge Label | ~(SF^OF) | 条件跳转(有符号数大于等于 >= 时跳转) |
| jl Label | SF^OF | 条件跳转(有符号数小于 < 时跳转) |
| jle Label | (SF^OF)|ZF | 条件跳转(有符号数小于等于 <= 时跳转) |
| ja Label | ~(SF^OF)&~ZF | 条件跳转(无符号数大于 > 时跳转) |
| jae Label | ~(SF^OF) | 条件跳转(无符号数大于等于 >= 时跳转) |
| jb Label | SF^OF | 条件跳转(无符号数小于 < 时跳转) |
| jbe Label | (SF^OF)|ZF | 条件跳转(无符号数小于等于 <= 时跳转) |
除了跳转指令,还有条件移动指令,和跳转指令类似,就是当满足条件的时候才进行 mov 操作,这里就不过赘述。我们重点来看看,如何用这些控制指令实现程序中的条件语句以及循环语句。
比如下面这个 C 函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
long lt_cnt = 0;
long ge_cnt = 0;
long absdiff_se(long x, long y)
{
long result;
if (x < y) {
lt_cnt++;
result = y - x;
} else {
ge_cnt++;
result = x - y;
}
return result;
}
我们其实可以用 goto 语句将其改写(这里只是出于演示目的,在实际生产中并不建议使用 goto):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
long lt_cnt = 0;
long ge_cnt = 0;
long gotodiff_se(long x, long y)
{
long result;
if (x >= y)
goto x_ge_y;
lt_cnt++;
result = y - x;
return result;
x_ge_y:
ge_cnt++;
result = x - y;
return result;
}
从改写的版本出发,我们就可以很容易读懂原程序对应的汇编指令:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
long absdiff_se(long x, long y)
x in %rdi, y in %rsi
absdiff_se:
cmpq %rsi, %rdi
jge .L2
addq $1, lt_cnt(%rip)
movq %rsi, %rax
subq %rdi, %rax
ret
.L2: x_ge_y:
addq $1, ge_cnt(%rip)
movq %rdi, %rax
subq %rsi, %rax
ret
循环也是类似的道理,比如下面这段 C 语言:
1
2
3
4
5
6
7
8
long fact_while(long n) {
long result = 1;
while (n > 1) {
result *= n;
n = n-1;
}
return result;
}
我们也是先考虑把它转化成 goto 的版本,这样更好理解最后生成的汇编指令
1
2
3
4
5
6
7
8
9
10
11
long fact_while_jm_goto(long n) {
long result = 1;
goto test;
loop:
result *= n;
n = n-1;
test:
if (n > 1)
goto loop;
return result;
}
对照着上面的 goto 版本,汇编指令可以直接写出:
1
2
3
4
5
6
7
8
9
10
fact_while:
movl $1, %eax
jmp .L5
.L6:
imulq %rdi, %rax
subq $1, %rdi
.L5
cmpq $1, %rdi
jg .L6
rep; ret
使用上述方式,我们还可以实现例如 for 循环,switch 控制语句,这里就不过多赘述,原理是一样的。
过程(Procedure)
一说过程,你可能一脸懵逼,这其实是一个抽象的说法,它有着诸多表现形式,常见的有函数、方法、执行单元等等,过程可以帮助我们对一些实现细节进行封装,以便于理解。一说到函数调用,估计人人都清楚,可是你知道计算机底层是如何处理函数调用的吗?我们需要从以下 3 方面入手:
- 控制逻辑是如何实现函数调用的
- 参数是如何传递的
- 函数调用是如何改变内存中的数据的
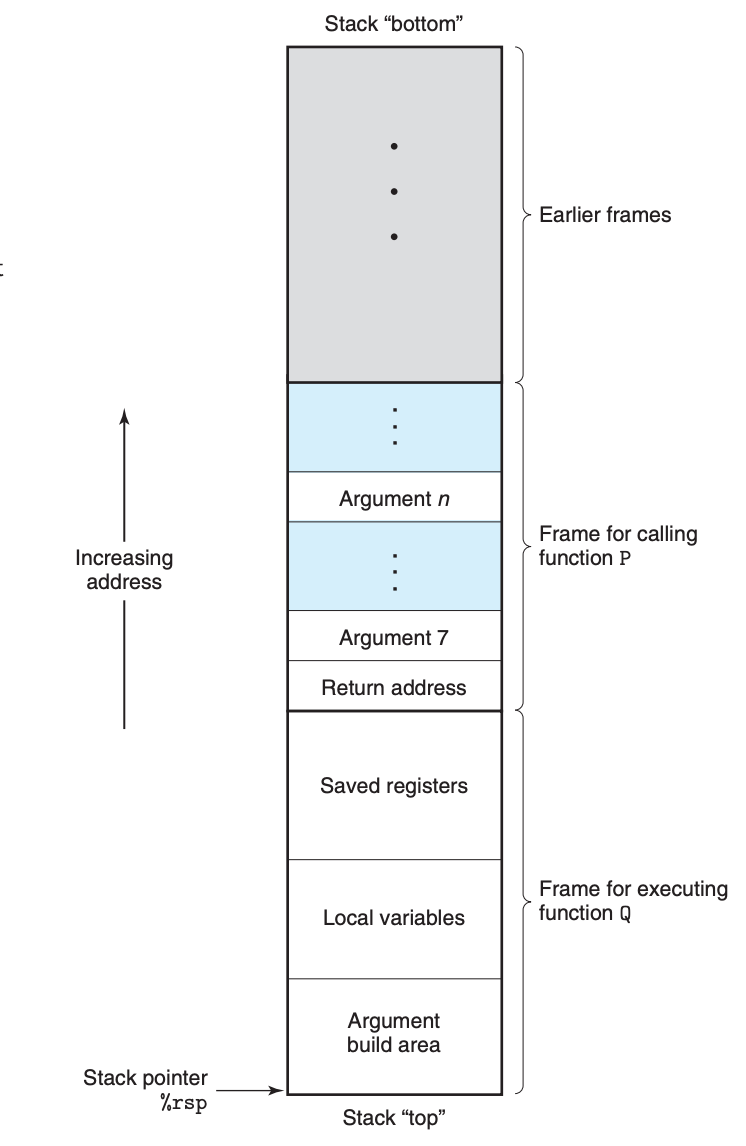
我们知道,函数调用离不开栈,那么在函数调用时,到底发生了什么,栈又是被如何更改的呢?下面这张图表示了栈上存储的和函数执行相关的元素:
其中,
- Argument 表示的是函数的参数,默认前 6 个参数存放在寄存器中,如果参数的个数超过 6 个,超过的部分会被放在栈上,并且可以看到,第 7 个参数被放到了栈顶,往上是第 8,第 9,以此类推。
- Return Address 表示的是当函数执行完毕,下一个要执行的指令的位置。
- Saved registers 指的是当函数要使用某些寄存器(callee-saved registers)时,在使用前,需要把这些寄存器上原有的数据存放在栈上,函数结束时再用栈上的数据对其恢复。这样在函数执行前后,寄存器中原有的数据就没有变化。
- Local variables 表示的是函数中的局部变量,当然局部变量也可以存放在寄存器中,这得视变量的数量以及编译器而定。
- Argument build area 是指当函数继续调用其他函数时,如果参数超过了 6 个,这一在这一区域继续类似前面 Argument 的操作。
可以看到,如果函数的参数和局部变量较少,并且也不调用其他的函数的话,其实是不需要用到栈的,完全依赖于寄存器即可,这也是最高效的方式。这么看来,简单短小的函数不仅仅更便于理解,运行效率也更高。
寄存器 %rbx,%rbp 还有 %r12 ~ %r15 被归为 callee-saved registers,也就是说被调用的函数需要保证这些寄存器在调用前后的数据一致。其他寄存器是 caller-saved registers,也就是调用的发起方需要去保证数据一致。
为了更好地理解函数调用和栈的关系,我们来看下面这个 C 程序:
1
2
3
4
5
6
7
long call_proc()
{
long x1 = 1; int x2 = 2;
short x3 = 3; char x4 = 4;
proc(x1, &x1, x2, &x2, x3, &x3, x4, &x4);
return (x1+x2)*(x3-x4);
}
上面的程序会生成如下的汇编代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
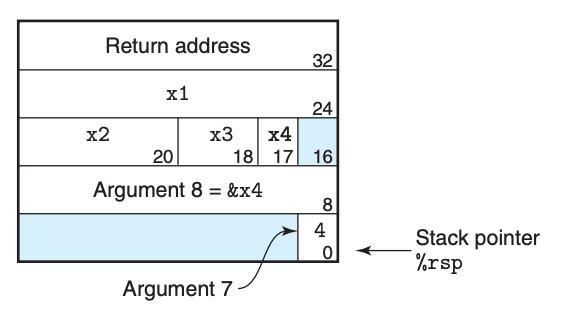
call_proc:
# 创建函数调用的变量
subq $32, %rsp
movq $1, 24(%rsp) # Store 1 in &x1
movl $2, 20(%rsp) # Store 2 in &x2
movw $3, 18(%rsp) # Store 3 in &x3
movb $4, 17(%rsp) # Store 4 in &x4
leaq 17(%rsp), %rax # Create &x4
# 参数传递 - 存在栈上
movq %rax, 8(%rsp) # Store &x4 as argument 8
movl $4, (%rsp) # Store 4 as argument 7
# 参数传递 - 存在寄存器中
leaq 18(%rsp), %r9 # Pass &x3 as argument 6
movl $3, %r8d # Pass 3 as argument 5
leaq 20(%rsp), %rcx # Pass &x2 as argument 4
movl $2, %edx # Pass 2 as argument 3
leaq 24(%rsp), %rsi # Pass &x1 as argument 2
movl $1, %edi # Pass 1 as argument 1
call proc
movslq 20(%rsp), %rdx # Get x2 and convert to long
addq 24(%rsp), %rdx # Compute x1+x2
movswl 18(%rsp), %eax # Get x3 and convert to int
movsbl 17(%rsp), %ecx # Get x4 and convert to int
subl %ecx, %eax # Compute x3-x4
cltq # Convert to long
imulq %rdx, %rax # Compute (x1+x2) * (x3-x4)
addq $32, %rsp # Deallocate stack frame
ret # Return
其中 call_proc 函数的调用栈就如下图所示:
另外一个问题就是,递归在底层又是如何实现的呢?其实递归就是函数调用自身,本身还是函数调用,比如下面这个 C 程序:
1
2
3
4
5
6
7
8
long rfact(long n) {
long result;
if (n <= 1)
result = 1;
else
result = n* rfact(n-1);
return result;
}
回生成如下的汇编代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# long rfact(long n)
# n in %rdi
rfact:
pushq %rbx # Save %rbx
movq %rdi, %rbx # Store n in callee-saved register
movl $1, %eax # Set return value = 1
cmpq $1, %rdi # Compare n:1
jle .L35 # If <=, goto done
leaq -1(%rdi), %rdi # Compute n-1
call rfact # Call rfact(n-1)
imulq %rbx, %rax # Multiply result by n
.L35: # done:
popq %rbx # Restore %rbx
ret # Return
可以看到,递归调用和其他函数调用没有任何区别,该做的事还是一样做。函数调用,本质上就是执行跳转指令,不同的是函数调用最后要回到函数调用处,并且会依赖于栈结构来存放临时信息。
数组的分配和访问
相比于其他语言,C 和底层接触的比较紧密。如果你了解 C 的话,应该清楚,C 中的数组和指针其实是一个东西,它们都是地址。假设一个数组 $x_A$,我们可以通过 $x_A + L * i$ 来访问下标为 $i$ 的元素。这个式子其实隐含着两个概念:
- $x_A$ 是数组的地址,也是数组中第一个(下标为 0)元素的地址
- $L$ 是数组中存放的数据类型的大小,比如对于一个类型为
int整形数组,$L$ 的大小就是 4
我们假设数组 E 的地址存放在 $\%rdx$ 寄存器中,它的下标 $i$ 存放在 $\%rcx$ 寄存器中。这样,我们可以将一些常见的 C 表达式对应到相应的汇编指令(表达式的结果存放在 $\%rax$ 中):
| 表达式 | 类型 | 值 | 汇编指令 |
|---|---|---|---|
| E | int * | $x_E$ | movl %rdx, %rax |
| E[0] | int | $M[x_E]$ | movl (%rdx), %eax |
| E[i] | int | $M[x_E + 4i]$ | movl (%rdx,%rcx,4), %eax |
| $\&E[2]$ | int * | $x_E + 8$ | leaq 8(%rdx), %rax |
| E+i-1 | int * | $x_E + 4i - 4$ | leaq -4(%rdx,%rcx,4), %rax |
| *(E+i-3) | int | $M[x_E + 4i - 12]$ | movl -12(%rdx,%rcx,4), %eax |
| &E[i]-E | long | $i$ | movq %rcx, %rax |
可以看到,这些数组/指针的操作在机器级指令中就是之前讲的 寻址操作,虽说我们计算地址时使用了类似加减法这样的算术运算,但是最终对应到汇编指令依旧是简单的移动和地址操作,这也是为什么使用指针或者数组会比其他数据结构更加高效的原因。
但是这里我们讲到的数组都是固定长度的,对于可变长度的数组,那么就没那么高效了,比如下面这个例子:
1
2
3
int var_ele(long n, int A[n][n], long i, long j) {
return A[i][j];
}
其中 n 是一个变量,并且 A 还是一个二维数组,上面的代码会生成下面的汇编代码:
1
2
3
4
5
6
7
# int var_ele(long n, int A[n][n], long i, long j)
# n in %rdi, A in %rsi, i in %rdx, j in %rcx
var_ele:
imulq %rdx, %rdi # Compute n * i
leaq (%rsi,%rdi,4), %rax # Compute xA + 4(n * i)
movl (%rax,%rcx,4), %eax # Read from M[xA + 4(n * i) + 4 * j ]
ret
其中的乘法指令 imulq %rdx, %rdi 会大大降低程序的效率,可这也是避免不了的。对于在循环中使用变量数组,编译器会做一些优化,比如下面这段 C 函数:
1
2
3
4
5
6
7
8
9
10
/* Compute i,k of variable matrix product */
int var_prod_ele(long n, int A[n][n], int B[n][n], long i, long k) {
long j;
int result = 0;
for (j = 0; j < n; j++)
result += A[i][j] * B[j][k];
return result;
}
首先编译器会将这段代码给优化成下面这样:
1
2
3
4
5
6
7
8
9
10
11
12
/* Compute i,k of variable matrix product */
int var_prod_ele_opt(long n, int A[n][n], int B[n][n], long i, long k) {
int *Arow = A[i];
int *Bptr = &B[0][k];
int result = 0;
long j;
for (j = 0; j < n; j++) {
result += Arow[j] * *Bptr;
Bptr += n;
}
return result;
}
提前把数组的地址计算出来,这样在后面的循环中,就不需要重复通过乘法指令来计算数组地址了,这段代码中循环对应的汇编指令如下:
1
2
3
4
5
6
7
8
9
10
# Registers: n in %rdi, Arow in %rsi, Bptr in %rcx
# 4n in %r9, result in %eax, j in %edx
.L24: loop:
movl (%rsi,%rdx,4), %r8d # Read Arow[j]
imull (%rcx), %r8d # Multiply by *Bptr
addl %r8d, %eax # Add to result
addq $1, %rdx # j++
addq %r9, %rcx # Bptr += n
cmpq %rdi, %rdx # Compare j:n
jne .L24 # If !=, goto loop
异质的数据结构
数组中的元素的类型统一,因而我们只需要知道元素的类型,很容易通过操作地址来访问数组中的元素。可是我们平常接触到的数据结构往往都可以存放多种类型的数据,常见的有链表的节点、树节点、图节点等等,那么这些数据结构在内存中又是如何存放的呢?我们如何定位呢?
这里介绍两个 C 中常见的数据结构—— structures 和 unions
Structures
在 struct 中,可以定义任意数量和类型的成员,这就类似于 C++ 和 Java 中的类(class),只不过类中还增加了方法。比如下面这个 struct:
1
2
3
4
5
6
struct rec {
int i;
int j;
int a[2];
int *p;
};
上面的结构所代表的连续空间就如下面这样:
如何操作这个结构中的各项元素呢?可以参照下面这段 C 代码:
1
2
3
int cal(struct rec *rp) {
return (*rp).i * (*rp).j;
}
因为这个操作太常见了,C 中也提供了一个简便的语法:
1
2
3
int cal(struct rec *rp) {
return (rp->i) * (rp->j);
}
那你可能会问,这个结构也是连续的,是不是我们也可以像操作数组那样,通过地址的计算来获取到具体的数据呢?理论上可以,但并不推荐,因为结构里面存放的成员都有着不同的大小,而且还会存在数据对齐的问题,这会导致地址的计算过于复杂。
不管是数组还是结构,到了机器指令层级(汇编层级),都没有任何的区别,机器指令仅仅需要知道的是,它需要操作某个寄存器,还是通过地址来操作内存。而如何将我们在高级语言(类似 C)中定义的这些结构,高效合理地转化成一条条机器指令,这都是编译器需要考虑的事。
Unions
union 可以说是 C 中一个非常古老的数据类型,这种类型在更高级的语言中基本已经看不到了。它可以让多个变量分享同一段数据,换句话说就是一段数据多重定义,比如下面这个例子:
1
2
3
4
5
6
7
8
unsigned long double2bits(double d) {
union {
double d;
unsigned long u;
} temp;
temp.d = d;
return temp.u;
}
上面的函数 double2bits 中的 temp 就是一个 union。它有两种表现形式,一个是 double,另一个是 unsigned long,也就是说这段 8 字节的数据(union 的大小为它表示的所有的成员中最大的),可以被解析为一个整数,也可以被解析为一个浮点数。当然,这段代码没有任何的意义,因为整形和浮点数的编码完全不一样,这里仅仅是为了做展示。
关于 union,还需要注意大小端的问题(我们在之前的文章中提到过大小端),比如下面这段代码:
1
2
3
4
5
6
7
8
9
double uu2double(unsigned word0, unsigned word1) {
union {
double d;
unsigned u[2];
} temp;
temp.u[0] = word0;
temp.u[1] = word1;
return temp.d;
}
上面这段代码在大端系统和小端系统上分别运行,会产生截然不同的结果。因为虽然都是更改 u 数组,但是最后 d 的解析顺序存在差异。这也是在使用 union 时需要注意的。
数据对齐
数据对齐指的是地址的对齐,主要是为了降低寻址操作的复杂性,从而提升效率。想象一下,在 64 位系统上,一块内存单元的大小就是 8 字节,CPU 每次都读取一块内存单元中的数据,这些数据的起始地址也当然都是 8 的倍数。如果说这时我们把一个 double 类型的数据存放在一个内存区块中,这样不管是读还是写,一条 mov 指令就够了,但是如果把这个数据放在起始位置不是 8 的地址上,也就是说这个数据被分割并存放在两个内存单元中,那样不管是读还是写,一条指令肯定不够,得两条。这里可能有个疑问,难道 CPU 就不能读起始地址不是 8 的倍数的数据吗?当然可以,但这就需要额外的判断了,增加了操作,降低了效率。
数据对齐的原则是,任何 K 字节的原型(primitive)对象,必须存放在为 K 的倍数的地址上。那如果不满足条件呢?那就往后推移,直到找到满足条件的地址。
比如说下面这个结构:
1
2
3
4
5
struct S1 {
int i;
char c;
int j;
};
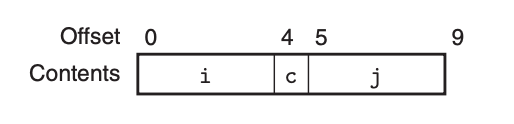
正常来说的话,也就是不考虑数据对齐,9 字节的空间足够了:
可问题是,第三个数据成员 j 存放的地址并没有对齐,因此我们需要填补空档,让其对齐:
可以看到,本来只有 9 字节的结构,考虑了数据对齐,最后的实际大小有 12 字节。其实我们完全可以调整数据成员的定义顺序来节省这部分空间,比如下面这样:
1
2
3
4
5
struct S2 {
int i;
int j;
char c;
};
S2 仅仅需要 9 字节,并且里面的每个成员都满足数据对齐的要求。这里有个优化技巧就是,将成员按照所占空间从大到小摆放,这样能保证最后的结果是最优的,也就是所需空间最少。
指针
上面我们说了各种各样的数据结构,这些数据结构都可以用指针来操作,而且我们也说过指针就是地址。很多人包括我自己会都会觉得指针就是汇编中我们看到的地址,然而实际上,C 中的指针是一层抽象,它并不直接等同于机器码中的地址。
这可以从下面这些特性看出:
- 如果一个指针的值为空,也就是
NULL(0),那么它并不指向任何地方。 - 类似于数组,指针运算会自动乘上模值,比如假设有一个指针
p它的值为q, 那么p+i的计算结果是q + L * i,其中L为这个指针所指向的元素的类型大小。 - 改变指针的类型并不会改变指针的值,假设指针
p的类型是char *,值为q,表达式(int *) p + 7的计算结果是q + 28,而表达式(int *) (p + 7)的计算结果是q + 7。 - 指针也可以指向函数,比如
int (*fp)(int, int *),这也好理解,函数其实就是代码在内存中的位置(地址)。
可以看到,即使是指针这么原始且底层的东西,依旧是层抽象,主要目的还是为了使用方便,并减少不必要的错误。
浮点数汇编指令集
上面我们所说的汇编指令集,包括寄存器单元都是针对整数的。而浮点数有另外一套指令集和寄存器单元。
首先来看寄存器单元:
这里每个寄存器的大小为 32 字节,即使是小的寄存器也有 16 字节,你可能会觉得奇怪,我们也没有这么大的数据类型啊?其实这主要是为一些并行处理提供方便,就是一个寄存器中存放多个数据,然后支持多条数据的读写。
再来看看浮点数的计算指令集,首先是移动指令:
| 指令 | 源 | 目的地 | 描述 |
|---|---|---|---|
| vmovss | $M_{32}$ | X | 针对单精度浮点数 |
| vmovss | X | $M_{32}$ | 针对单精度浮点数 |
| vmovsd | $M_{64}$ | X | 针对双精度浮点数 |
| vmovsd | X | $M_{64}$ | 针对双精度浮点数 |
| vmovaps | X | X | 寄存器对应位置的移动(单精度) |
| vmovapd | X | X | 寄存器对应位置的移动(双精度) |
浮点数之间的移动好说,但是平时计算少不了整形和浮点型之间的类型转换,这又如何处理呢?其实也简单,有专门的指令负责这个事情:
浮点数到整形的转化:
| 指令 | 源 | 目的地 | 描述 |
|---|---|---|---|
| vcvttss2si | X/$M_{32}$ | $R_{32}$ | 将单精度浮点数转化成 4 字节的整形 |
| vcvttsd2si | X/$M_{64}$ | $R_{32}$ | 将双精度浮点数转化成 4 字节的整形 |
| vcvttss2siq | X/$M_{32}$ | $R_{64}$ | 将单精度浮点数转化成 8 字节的整形 |
| vcvttsd2siq | X/$M_{64}$ | $R_{64}$ | 将单精度浮点数转化成 8 字节的整形 |
整形到浮点数的转化(因为我们只使用浮点数寄存器中前 32 个 bit 位,所以 源 2 并不会被用到):
| 指令 | 源 1 | 源 2 | 目的地 | 描述 |
|---|---|---|---|---|
| vcvtsi2ss | $M_{32}$/$R_{32}$ | X | X | 将 4 字节的整形转化成单精度浮点数 |
| vcvtsi2sd | $M_{32}$/$R_{32}$ | X | X | 将 4 字节的整形转化成双精度浮点数 |
| vcvtsi2ssq | $M_{64}$/$R_{64}$ | X | X | 将单精度浮点数转化成 8 字节的整形 |
| vcvtsi2sdq | $M_{64}$/$R_{64}$ | X | X | 将单精度浮点数转化成 8 字节的整形 |
除此之外浮点数也有类似的算数计算指令:
| 指令(单精度) | 指令(双精度) | 功能 | 描述 |
|---|---|---|---|
| vaddss | vaddsd | D <- S2 + S1 | 浮点数加法 |
| vsubss | vsubsd | D <- S2 - S1 | 浮点数减法 |
| vmulss | vmulsd | D <- S2 x S1 | 浮点数乘法 |
| vdivss | vdivsd | D <- S2 / S1 | 浮点数除法 |
| vmaxss | vmaxsd | D <- max(S2,S1) | 浮点数取最大值 |
| vminss | vminsd | D <- min(S2,S1) | 浮点数取最小值 |
| sqrtss | sqrtsd | D <- sqrt(S1) | 浮点数取平方根 |
比如说下面这个 C 函数:
1
2
3
double funct(double a, float x, double b, int i) {
return a*x - b/i;
}
生成的汇编代码如下:
1
2
3
4
5
6
7
8
9
10
11
# double funct(double a, float x, double b, int i)
# a in %xmm0, x in %xmm1, b in %xmm2, i in %edi
funct:
# The following two instructions convert x to double
vunpcklps %xmm1, %xmm1, %xmm1
vcvtps2pd %xmm1, %xmm1
vmulsd %xmm0, %xmm1, %xmm0 # Multiply a by x
vcvtsi2sd %edi, %xmm1, %xmm1 # Convert i to double
vdivsd %xmm1, %xmm2, %xmm2 # Compute b/i
vsubsd %xmm2, %xmm0, %xmm0 # Subtract from a*x
ret # Return
另外,在 x86-64 中,浮点数指令并不能直接处理常量,浮点数常量需要借助代码寄存器(%rip)。比如下面这个 C 函数:
1
2
3
double cel2fahr(double temp) {
return 1.8 * temp + 32.0;
}
生成的汇编代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
# double cel2fahr(double temp)
# temp in %xmm0
cel2fahr:
vmulsd .LC2(%rip), %xmm0, %xmm0 # Multiply by 1.8
vaddsd .LC3(%rip), %xmm0, %xmm0 # Add 32.0
ret
.LC2:
.long 3435973837 # Low-order 4 bytes of 1.8
.long 1073532108 # High-order 4 bytes of 1.8
.LC3:
.long 0 # Low-order 4 bytes of 32.0
.long 1077936128 # High-order 4 bytes of 32.0
除了上面列的这些,浮点数也需要考虑诸如函数参数传递、比较、位移等等整形当中的常规操作,这些都大同小异,这里就不展开了。最主要的是要清楚,浮点数和整数的指令集完全是不同的,并且浮点数的指令集要复杂的多,效率相对来说也比较低。因此,在实际当中,能用整形解决的问题就不要用浮点数了。