计算机中的数据表示
前言
这篇文章的所有内容均出自 CSAPP 的第二章,主要讲解数据的存储和表示,算是对这部分内容的总结回顾。我们知道,计算机中的数据说到底都是 0,1 这样的二进制流,而这样的二进制流是如何表示我们熟悉的事物的呢?比如程序中的整形、浮点数以及字符串,还有二进制是如何支持变量计算的呢?这篇文章通通会给出答案。
关于这部分内容,很多书籍都会给出一句话,如果你接触过计算机,相信你或多或少也听过,这句话是 “负数的补码是正数的原码取反再加一”,如果细挖,什么是补码?什么是原码?为什么可以这样转化?它们互相转化的意义何在?当你没有了解底层逻辑时,你是回答不上这些问题的,这句话也就只能对照着帮你做做简单练习题,但想要正真理解这句话所反应的本质,我们就需要追根溯源,学习二进制流的存储以及表示。
数据的存储
字长
计算机系统中有个 字长(word size) 的概念,可能你没有太多印象,但是一说到 32 位的系统,64 位的系统,你应该就懂了,这里的 32 和 64 就是计算机的字长。那这个字长表示的又是什么呢?
计算机中的一个重要概念就是 地址,C 和 C++ 这种比较偏底层的语言允许程序直接操作地址(指针就是地址)。但是这个地址其实是内存的虚拟地址(virtual memory address),并不是实际的物理地址,这个解释起来比较复杂,你可以简单吧虚拟地址理解为一层抽象,操作系统将虚拟地址和实际的物理地址一一映射起来,上层用户(程序)只需提供虚拟地址给操作系统,其他的交由操作系统处理即可。字长则决定了计算机的整个虚拟地址的长度,虚拟地址的范围是 $ 0 ~ 2^w - 1 $ 其中 $ w $ 是计算机的字长,也就是说字长也决定了实际地址的访问长度。
也就是十几年前,个人电脑普遍使用的还是 32 位的系统,整个虚拟地址的长度是 $ 2^32 $ 也就是 4 GB,所以那个时候内存所支持的最大容量就是 4 GB。但是随着科技,尤其互联网技术的发展,这么点内存肯定不够啊,所以字长增加到了 64,可支持的虚拟地址的长度是 16777216 TB,在目前看来,这完全够用了。同时,64 位的系统其实是兼容 32 位的,32 位系统上编写的程序放到 64 位系统上依然可以照常运行,因为 32 位系统里的所有地址都可以在 64 位系统中表示,但反过来就不行,这也好理解。
字节
位(bit)是计算机中的最小单位,这没错,但是要说数据存储和表示的最小单位,那就得是字节(Byte),一个字节由 8 个 bit 组成。编程语言中的数据类型的大小也是以字节为基本单位,就拿 C 语言来说,int 的大小是 4 bytes,char 的大小是 1 bytes,double 的大小是 8 bytes 等等。有时我在想为什么是字节呢?一个字节为什么会有 8 个 bit 呢?
这其实就相当于一个协议,单个 bit 只能表示 0,1 两种情况,如果以 bit 为数据表示的基本单位,那数据的长度就太不好统一了,这会给数据的读取造成不小的麻烦,就比如 CPU 跑到内存中读取一个数据,那到底是读取几个 bit 呢,1 个?2 个?32 个?还是更多?以字节为单位可以大大缩小情况的个数。你也许会说,本来 0 这个数值用 1 个 bit 就可以表示,但是你却非要用 8 个 bits 甚至更多的空间来表示,这不是存在着空间的浪费吗?的确,但这其实是在用空间换时间,底层计算机指令只需去到对应的地址获取固定大小的数据即可,不需要再进行任何的转换或者判断。
再比如我们常说的存储单位,比如 KB、MB、GB、TB 等等,这里的 B 就是指的字节,可见字节这个概念是计算机数据存储与表示的基本单位。
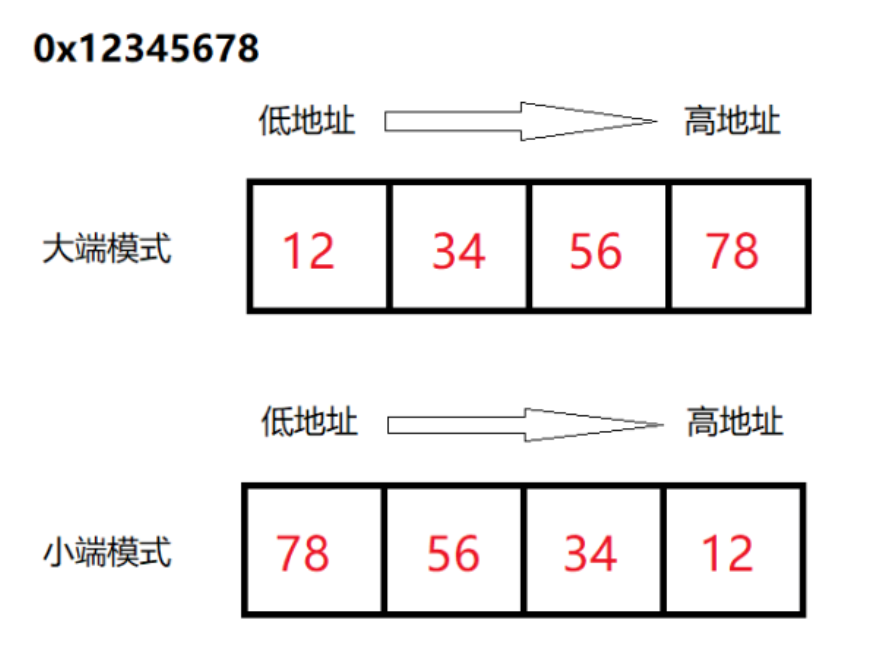
大小端
清楚了字节的概念,大小端这个东西就好解释了。怎么说呢?还是拿生活中常见的例子来说,在 Windows 以及 Mac 中都会有图形窗口,但是不一样的是,Windows 图形窗口的关闭以及缩小选项位于图形窗口的右上角,Mac 则不一样,同样的选项位于窗口的左上角。另外,在 Windows 和 Mac 中用户都可以通过鼠标的滚动来上下浏览页面,Windows 鼠标滚动方向和页面滚动方向一致,Mac 则是相反的。可见不同公司设计的产品,在很多的细节上都是对立的。
大小端则是指的是数据的字节存放顺序。大端会将这个数据的高位作为起始位置进行存放,而小端则相反,把数据的低位作为起始位置存放。就拿一个大小为 4 字节的 int 类型的数据 0x12345678 来说:
大小端主要由 CPU 决定,比如 Intel 公司生产的 CPU 是小端模式,而之前 IBM 公司旗下的一些 CPU 则是大端模式。
当你想要判断 CPU 是小端还是大端,也非常简单,你仅读取一个数据的第一个字节,如果这个字节存放的是该数据的高位,那么就说明是大端模式,反之,则是小端模式,下面这段程序就可以判断 CPU 的大小端:
1
2
3
4
5
6
7
8
9
int main() {
int i = 1;
char *p = (char *) &i;
if (*p == 1) {
printf("小端模式");
} else if (*p == 0) {
printf("大端模式");
}
}
你可以试一试,Intel 和 AMD 的 CPU 均为小端模式。
数据的存储与表示的关系
我们前面说过计算机的一切数据都是二进制流,但是计算机展现给我们的要比这简单的二进制流丰富的多,这又是为什么呢?
其实这就看你如何对二进制流进行解释了,对于一段相同的二进制流,我们可以将其转化成整数,可以按照 IEEE 标准(我们后面会讲到)转化为浮点数,也可以通过 ASCII 码转化成字符串,我们还可以将其看作是机器级别的指令。一段数据是什么其实并不单单取决于这段数据本身,还取决于这段数据的执行上下文环境,一段冷冰冰的二进制流被附加上各种各样的解释、规则、协议后,它们就会被转化成丰富多彩的内容,这也是计算机好玩、有趣且有着无限潜力的根本原因。
数据的表示
整数的表示
常见的整数类型
拿 C 语言来说,比较常用的类型有下面这些,以及这些类型所占用的存储空间,可表示的范围(最小值~最大值):
| 类型 | 大小(Byte) | 最小 | 最大 |
|---|---|---|---|
| char | 1 | -128 | 127 |
| unsigned char | 1 | 0 | 255 |
| short | 2 | -32,768 | 32,767 |
| unsigned short | 2 | 0 | 65,535 |
| int | 4 | −2,147,483,648 | 2,147,483,647 |
| unsigned | 4 | 0 | 4,294,967,295 |
| long | 8 | −9,223,372,036,854,775,808 | 9,223,372,036,854,775,807 |
| unsigned long | 8 | 0 | 18,446,744,073,709,551,615 |
需要特别说明的是,上表中的数值都是基于 64 位系统,如果是 32 位系统的话,long 的大小会是 4 bytes,这也就导致 long 类型成为了一个不可移植的类型,为此,C 中由特别引入了 int64_t,uint64_t,int32_t,uint32_t,这些类型的大小固定,不会因为系统的位数而改变。
很有意思的一点是,这些默认支持类型的大小均不超过系统的位数。这也很好解释,系统自带的汇编指令集囊括了针对这些数据类型的指令,如果大小超出了系统位数,同样的数据操作,底层需要执行多条指令来完成,效率会大打折扣。
无符号数的编码
通过上面的表,我们可以看出同样的类型都存在一个无符号的类型,与有符号类型相比,大小一样,但是表示的范围不同(这一点后面会解释)。无符号数的编码方式其实就是普通的二进制的编码方式,比如 0010 表示的是 2,0111 表示的是 7。我们可以把一个整形数看作是一个向量 $\vec{x}$:
这里的 $w$ 表示的是类型的 bit 总数,比如对于 unsigned int 来说的话,$w$ 就是 32,对于 unsigned long 来说的话,$w$ 就是 64。这个向量表示的数可以通过下面的式子计算得出:
无符号数的表示范围是从 0 到 $2^w - 1$,这也不难得出。
2 的补码
虽然说无符号数的编码非常直接,和我们看到的十进制表示一样,但是在计算机中负数又该如何表示呢?毕竟计算机中只有 0 和 1,想要表示负数,我们则需要建立一个新的规则。
我们还是把一个数看作是以 bit 为基本单位的向量 $\vec{x} = [x_{w-1},x_{w-2},…,x_0]$,无论规则是什么,有一个前提条件必须保证,那就是 向量和数是一对一的关系。另外还有一点,我们希望表示的负数个数尽可能和正数相同,由此我们得到了一种方式,将 $x_{w-1}$,也就是最高位看作是负数,其他位的计算方式还是和无符号数一样,这样最后表示的数值就可以通过下式计算得出:
\[B2T_w(\vec{x}) = -x_{w-1}2^{w-1} + \sum_{i=0}^{w-2}x_i2^i\]因为对于任意一个非负数 $x$,把 $2^w - x$ 在正常编码(无符号数编码)下的二进制流放到这个规则下就是它的负数 $-x$,所以这种编码方式被称作 2 的补码的编码(Two’s-Complement Encodings)。
通过上面的式子,我们也可以看出,在这个规则下,对于一个正数,$-x_{w-1}2^{w-1}$ 为 0,该项不存在,所以其实等同于无符号数的表示。
另外,表示最小值的向量是 [1,0,0,...,0],代表的整数就是 $ -2^{w-1} $,表示最大值的向量是 [0,1,1...,1],代表的整数为 $ 2^{w-1} - 1 $。这也是为什么之前的表中,有符号数的范围,最小值的绝对值总是比最大值多一。当然,如果把 0 也看作是正数,那么负数和正数的表示个数就相同了,这也正是我们想要的。
有了这些知识,回到那句著名的定理 负数的补码是正数的原码取反再加一,这里的 负数的补码 就是我们要的,也就是上面式子中的 $B2T_w(\vec{x})$,而 原码 则是一个数的最基本二进制表示,也就是无符号数的表示形式。那么为什么在这种编码方式下,正数的原码取反加一就是负数呢?
首先是取反操作,假设原码所表示的值是 $a$,取反后最高位所表示的值为 $-2^{w - 1}$,而其他位所表示的值为 $2^{w - 1} - 1 - a$(其中 $2^{w - 1} - 1$ 表示的是 [0,1,1,1,...,1],减去 $a$ 则表示除最高位的取反),所以取反后的值就为二者之和,也就是 $-2^{w - 1} + 2^{w - 1} - 1 - a$ 也就是 $-1-a$,将其加上 1,就是 $-a$。
是不是理解这里的规则后,不需要之前的 “定理”,也可以很容易通过推导得出答案。这个规则仅仅是改变了最高位的意义,将其从原来的正值改为了负值,仅此而已。
有符号数与无符号数之间的转换
我们之前说过,不同的二进制流,解释的规则不同,所代表的事物也就不同。就好像同样的二进制向量 $\vec{x} = [x_{w-1},x_{w-2},…,x_0]$,在无符号数的编码下,它可能是一个很大的正数,而在有符号数(2 的补码)编码下,可能就是一个负数。在二进制流不变的前提下,有符号数和无符号数是如何对应起来的呢?
当一个数为有符号数可表示范围内的正数时,有无符号数与无符号数的二进制编码一样,所代表的值也一样,这没什么好说的。
当一个有符号数为负数时,它的无符号数的值就是 $T2U_w(x) = x + 2^w$,反过来也一样,当一个无符号数的表示超过了有符号数的表示范围,也就是 TMax < u,那么有符号数的值就是 $U2T_w(u) = u - 2^w$。
这些都可以从之前的两个公式推导出来,不想推的话,举几个例子也很容易理解,比如 [1,1,1,1,...,1] 在有符号数中表示的是 -1,而在无符号数中则表示的是最大值 $2^w - 1$,再比如 [1,0,0,0,...,0] 在有符号数中表示的是最小值 $-2^{w-1}$,而在无符号数中表示的是 $2^{w-1}$。
不同数据类型之间的转换
通过前面的那张表,我们知道虽然都是整数,但是不同类型所占用的空间不一样,可表示的数据范围也不一样。
这里比较好理解的是从小到大的转化,比如从 int 到 long 的转换,如果是无符号数,只需要将在前面填补 0 即可,也就是
如果是有符号数,只需要在前面填补最高位,也就是
\[\vec{x} = [x_{w-1},x_{w-2},...,x_0] -> \vec{x}' = [x_{w-1},...,x_{w-1},x_{w-1},x_{w-2},...,x_0]\]这很好理解,因为有符号数编码下的 $[x_{w-1},0,0,…,0]$ 和 $[x_{w-1},…,x_{w-1},0,0,…,0]$ 所代表的值是一样的。
但是当我们从大到小进行转换,问题就出现了。我们必须要考虑到数据丢失的问题,先来说说无符号数,当一个无符号数 $\vec{x} = [x_{w-1},x_{w-2},…,x_0]$,经过转换后变成了 $\vec{x}’ = [x_{k-1},x_{k-2},…,x_0]$,其中 $k < w$。这里 $x$ 与 $x’$ 的关系是 $x’ = x mod 2^k$,因为对于任意的 $i$,这里 $i>=k$,$ 2^i mod 2^k = 0$。
有符号数也是类似的,只不过最高位变成了符号位(负值)。可以先将其看成是无符号数,并做一样的处理,也就是 $x’ = x mod 2^k$,然后在将其转换成有符号数,合起来就是 $x’ = U2T_k(x \ mod \ 2^k)$。
当然,在 C 语言中,不同数据类型的转换还会造成一些陷阱,比如 -1 < 0U 的结果是 false,这是因为当一个表达式中同时出现有符号数和无符号数,C 会默认将有符号数看作是无符号数,然后在执行操作。
另外,C 语言会先进行类型大小的转换,然后才是有符号和无符号的转换,比如下面这个例子:
1
2
3
4
5
short sx = -12345;
unsigned uy = sx; // -> (unsigned)(int) sx
printf("uy = %u:\t", uy); // 4294954951
show_bytes((byte_pointer) &uy, sizeof(unsigned)); // 0xFFFFCFC7
这里 -12345 先进行大小的转换,有符号数扩充在前面填补最高位,扩充后所表示的数又直接转成了无符号数(二进制不变),这也就导致了最后的结果和我们设想的不一样。
整数的运算
前面说了整数的二进制表示规则,而这些二进制是如何参与整数的计算的呢?不同的运算会如何对二进制流进行改变呢?这也是这一小节要讨论的问题。
加法运算
早在小学我们就学过十进制的加法运算,加法运算总结下来就是 从低位到高位,对位相加,逢十进一。换做是二进制,也是类似的,只不过之前的 “逢十进一” 变成了 “逢二进一”。
这个计算规则是没错,但是放到程序当中,我们还需要考虑数据类型的大小,如果相加后的数超过了该类型的表示范围该如何处理?还有就是有符号数(2 的补码)的编码方式会对运算后的二进制带来什么样的改变?
我们还是先来看看无符号数的加法,这其实就是正常的二进制加法,只不过我们需要考虑溢出。假设有 $x$ 与 $y$ 两个数,并且 $0<=x,y<2^w$,如果说 $x+y<2^w$,加法后的结果没有超过数据类型的范围,那么我们可以得到准确的结果,也就是 $x+y=x+y$。但是如果 $2^w<=x+y<2^{w+1}$,这时发生了溢出,超过可表示范围的位将被丢弃,最后剩余的二进制流所表示的值其实是 $x+y=x+y-2^w$。
另外一个问题是,在程序中我们如何确定两个无符号数的加法运算发生了溢出呢? 这其实可以通过数学推导得出,假设 $s=x+y$,因为 $0<=x,y$,所以如果运算正常的话,$s>=x$ 并且 $s>=y$。但当溢出发生时,$s=x+y=x+(y-2^w)<x$,同样地,$s=x+y=y+(x-2^w)<y$,所以我们只需要比较 $s$ 和 $y$ 或者 $x$ 的大小关系就可判定是否运算发生了溢出。
说完无符号数,我们再来看有符号数。也是假设有两个数 $x$ 与 $y$,两个数均在可表示的范围内 $-2^{w-1} <= x,y <= 2^{w-1} - 1$。$x+y$ 的结果有以下 3 种情况:
- 第一种是正常情况,$-2^{w-1} <= x+y <= 2^{w-1} - 1$,这时不存在溢出,$x+y=x+y$
- 第二种是正溢出,$x+y >= 2^{w-1}$,这其实和无符号数类似,正数表示范围内已经满了,只能向最高位进一,而在有符号数(2 的补码)的编码下,最高位为负值,也就是本身应该是正值的位被当成了负值,这一来一去相当于在原数的基础上减去了 $2^w$,最终 $x+y=x+y-2^w$,这结果和前面的无符号数溢出一样
- 第三种是负溢出,$-2^{w-1} > x+y$,也就是负数位(最高位)没法表示当前的计算后数值了,负数位往前进 1,最终 $x+y=x+y+2^w$
同样的,假设 $s=x+y$,我们也可以通过比较 $s$ 和 $x$,$y$ 来判定结果是否存在溢出。当 $x,y>0$ 但是 $s<=0$ 则说明存在正溢出,而 $x,y<0$ 但是 $s>=0$ 则说明存在负溢出,可以自行推导,这里就不过多赘述。
整数的非
先来看看对于非的定义,对于给定任意一个 $x$,总存在一个值 $-x$,使得 $-x + x = 0$,这里的 $-x$ 就与 $x$ 互为非。那么给定一个整数,它的非是多少,二进制的表示又是如何的呢?
对于这个问题,我们还是需要分情况讨论,因为编码方式的差异导致同样的二进制表示的值的范围的不一样,所以最后的结果也可能存在出入。
首先来看无符号数的非,给定一个无符号数 $x$,并且在可表示的数值范围内,也就是 $0 <= x < 2^w$,存在以下两种情况:
- 当 $x=0$ 时,这时 $x$ 的非就是它本身,$-x=0$
- 当 $x>0$ 时,因为 $-x+x=0$,但是无符号数没法表示负数,因此 $-x+x$ 必须发生溢出才会使等式成立,之前讲过,无符号数加法发生溢出时,$-x+x=-x+x-2^w$,如果要使 $-x+x-2^w=0$,那么 $-x = 2^w-x$
有符号数的非相对来说要复杂些,假设一个有符号数 $x$,并且 $-2^{w-1}<=x<=2^{w-1}-1$,存在以下两种情况:
- 当 $x = -2^{w-1}$,因为有符号数(2 的补码)编码的不对称性,导致非并不等同于数值上的非,这时还得借助溢出,这里的 $-x=x=-2^{w-1}$
- 当 $x > -2^{w-1}$,很明显,$-x=-x$
对于有符号数来说,还有两个确定非的方法,这两个方法都是从 bit 层面来考虑的。回想下之前的那句话 负数的补码是正数的原码取反再加一,这里的正数与负数互为非:
- 直接将上面的 “定理” 转化成数学表达式也就是
-x = ~x + 1 - 假设最右边的 1 是在第 $k$ 位,对应的整数的 bit 向量是 $[x_{w-1},x_{w-2},…,x_{k+1},1,0,…,0]$,那么这个数的非的二进制向量就是第 $k$ 位以及左边的位不变,其余位取反 $[\sim x_{w-1},\sim x_{w-2},…,\sim x_{k+1},1,0,…,0]$
上面两个技巧其实都可以通过 2 的补码的性质加上数学推导得出,它们很多时候可以帮助我们快速求解。
整数的乘法
乘法很容易导致溢出,但是这里无符号数和有符号数可以放在一起讨论。有符号数的乘法运算可以先将乘数看成是无符号数来对 bit 位进行更改,然后在转为有符号数(二进制结果不变)。对无符号数来说,结果是实际结果与最高位的下一位的余也就是 $xy=(xy)mod2^w$,二进制成面有符号数没有差别,只不过最后改变一下解释规则,也就是 $xy=U2T_w((xy)mod2^w)$。
需要知道的是,乘法其实是一个开销比较大的运算,很多时候编译器会对乘法做一些优化,比如试着将其转换为左移操作。因为对于无符号数和有符号数来说 $x«k$ 等同于 $x * 2^k$。
假设计算 $xy$,$y$ 的二进制表示中第 $m$ 位到第 $n$ 位全为 1,其余位全为 0,大致的形式就是 0,...,0,1,...,1,0,...,0,这时就可以借助左移操作将 $xy$ 转换成下面的式子:
其实就是
\[(x<<(n+1)) - (x<<m)\]这样一个乘法就变成了两个位移和一个加(减)法运算,这可以大量减少底层机器指令的计算操作。当然了,这只是一个特殊的例子用来说明位移和乘法的关系。
整数的除法
两个变量的除法不存在溢出,也就没什么好说的。但是和乘法类似,除法也可以通过位移操作来达成,和除法对应的是右移操作,因为编解码的不同,存在两种右移——逻辑右移和算术右移,逻辑右移在最高位补 0,算术右移在最高位补上之前的最高位,这两种位移对应着无符号数和有符号数的除法。当然,很多语言并不支持无符号数,也就没有所谓的逻辑右移,只有算术右移。
对于无符号数和有符号数来说,$x » k$ 的值是 $\lfloor x/2^k \rfloor$。但是这个操作下,有符号数会产生一些和正常整数除法不同的结果,比如 $-3/2$ 正常情况下会得到 $-1$,但是 $-3 » 1$ 的结果是 $-2$,这并不是我们想要的,而对于有符号数来说 $(x + (1 « k) - 1) » k$ 会得到 $\lceil x/2^k \rceil$,所以在 C 中如果要通过位移操作来计算 $x/2^k$,正确的表达式应该是
1
(x<0 ? (x+(1<<k)-1) : x) >> k
整数运算的一些陷阱列举
基于整数编码的性质,下面列举了一些案例:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
int x = foo(); // Arbitrary value
int y = bar(); // Arbitrary value
unsigned ux = x;
unsigned uy = y;
(x&7) !=7 || (x<<29 < 0) // Always True
x < 0 || -x <= 0 // Always True
x+y == uy+ux // Always True
x*~y + uy*ux == -x // Always True
(x>0) || (x-1<0) // False when x = TMin
(x*x) >= 0 // False when x = 0xFFFF
x > 0 || -x >= 0 // False when x = TMin
在编程时,我们尽量将变量转换成同一类型后在进行运算,这样能减少隐藏的 bug。另外,我们也需要考虑到有符号数(2 的补码)编码方式下的特殊情况,比如最小值等等。
浮点数的表示
二进制流如何表示小数呢?我们先来看看小数的展现形式:
\[b_mb_{m-1}...b_1b_0.b_{-1}b_{-2}...b_{-n+1}b_{-n}\]以最中间的小数点为分界线,小数点左边是整数部分,小数点右边则是浮点数部分。最终的值可以通过各项加权得到:
\[b = \sum_{i=-n}^{m}2^i * b_i\]对比之前的整数,只不过是加权求和的起始从 0 变成了 -n,这个式子给了我们表示浮点数的方向。用二进制表示浮点数的方式方法有很多,但如果没有一个统一的标准,那岂不是乱套了?为此,IEEE 在 754 号标准中做了统一,二进制浮点数可以表示成 $V = (-1)^s * M * 2^E$,可以类比 科学计数法 其中:
- $V$ 是最后浮点数的值
- $s$(Sign),符号位,用来决定该数是正还是负
- $M$(Mantissa),尾数,这是一个小数,范围为
[1,2)或者是[0,1)(有两种可能,后面会给出解释) - $E$(Exponent),指数,可以看作是一个无符号整数
上面的 $s$,$M$,以及 $E$ 共同决定了一个浮点数的值,它们的大小都存放在二进制流中,具体如下图所示:
单精度浮点数和双精度浮点数对应到 C 中的 float 和 double,由上图可知它们的大小区别主要在 $E$ 和 $M$ 上,$E$ 的物理空间大小代表着数的表示范围的大小,$M$ 的物理空间大小一定程度上决定了精度。双精度在范围和精度上都要优于单精度,这时肯定的,毕竟用了双倍的空间。
有了上面的定义就完事了吗?你仔细想想就知道,上面的式子仅仅给了个框架,除此之外还有很多不清楚的地方。就比如 0 如何表示?如果只看定义,只要 $M$ 部分为 0,$s$ 和 $E$ 随便给都是 0。还有,最后的值的很大程度上是 $M$ 和 $E$ 共同决定的,那貌似同样一个数值可以由多种 $M$ 和 $E$ 的组合决定,那如何才能保证二进制流和数值一一对应呢?
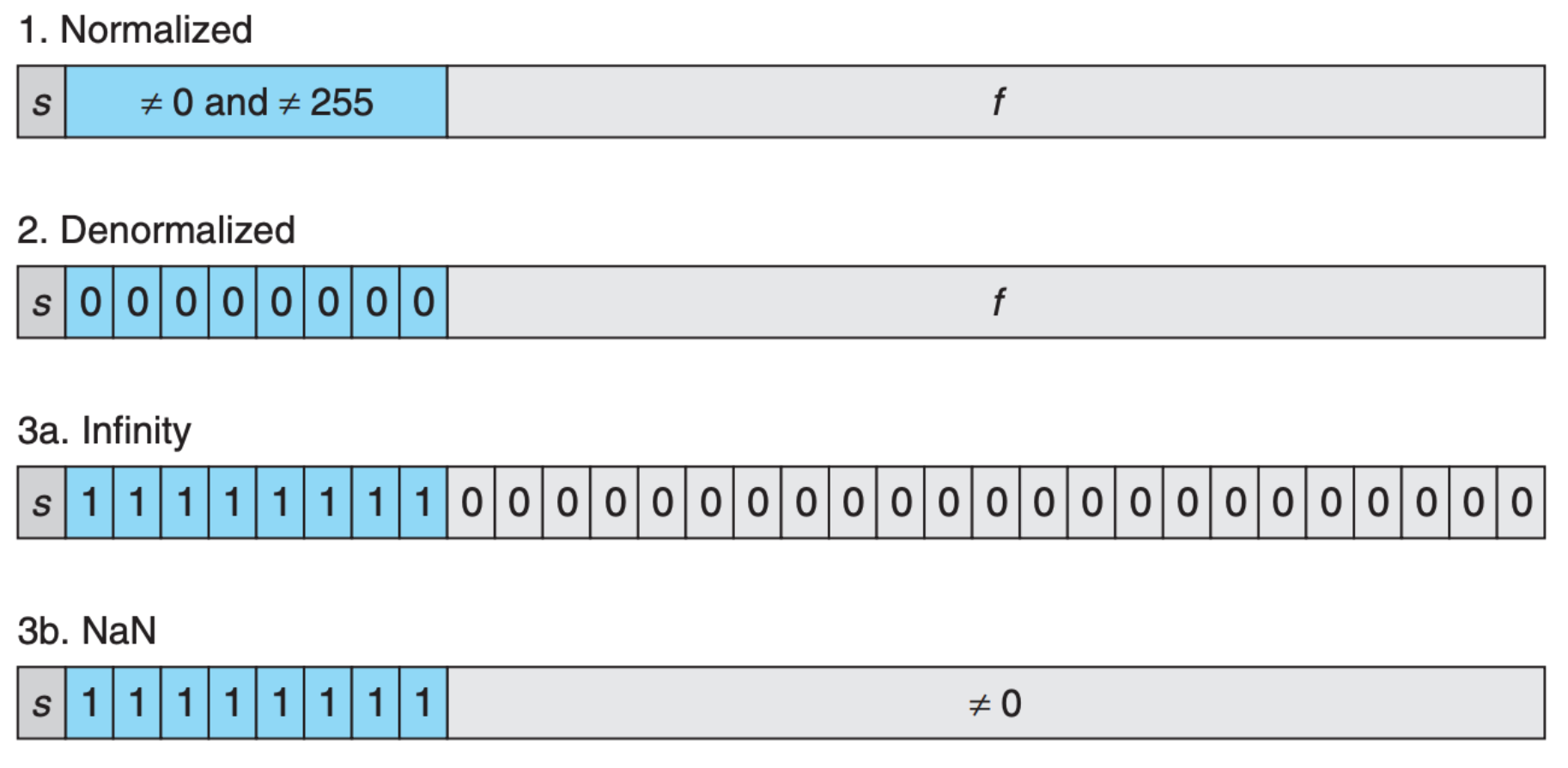
基于上面提到的问题,IEEE 标准又给出了下面 3 种情况,并对 $E$ 和 $M$ 所表示的值作了些限定,我们假设指数部分为 $e_{k-1}…e_1e_0$,尾数部分为 $f_{n-1}…f_1f_0$:
- 情况 1(Normalized):当 $e_{k-1}…e_1e_0$ 表示无符号数不为 0 也不为最大值($2^{k} - 1$)时,$E = e_{k-1}…e_1e_0 - Bias$,这里的 $Bias$ 是一个固定值,大小为 $2^{k-1} - 1$。另外 $M=1.f_{n-1}…f_1f_0$,这时 M 的取值范围为
[1,2)。 - 情况 2(Denormalized):当 $e_{k-1}…e_1e_0 = 0$ 时,也就是所有的指数部分的 bit 均为 0,这时 $E = 1 - Bias$,$M=0.f_{n-1}…f_1f_0$,这时 M 的取值范围为
[0,1)。 - 情况 3(Special):当 $e_{k-1}…e_1e_0$ 表示无符号数为最大值($2^{k} - 1$)时,也就是所有的指数部分的 bit 均为 1,这时有两种情况:
- 情况 3.1(Infinity):当 $M=0$ 时,也就是 M 部分的 bit 全为 0 时,整个数表示的是无穷,前面的符号位决定是正无穷还是负无穷。
- 情况 3.2(NaN):当 $M\not=0$,这时表示的是不是数字(Not a Number),通常用来表示计算出错
下图可以很好地总结上面列出的几种情况(以单精度浮点数为例):
看了上面列的这些情况,你可能还是一头雾水,有必要弄得这么复杂吗?
这里还是来讨论几个问题,首先是 为什么指数部分要弄个偏量 $Bias$ 出来? 这其实就是为了让指数部分也能表示负值,有了这个偏移量,$E$ 的范围就变成了 [-126,127](双精度为 [-1022,1023]),这样就可以表示更小的数了。那为什么不直接用我们前面讲的有符号数(2 的补码)的编码方式来编码呢?主要原因还是因为有符号整数的编码比较复杂,需要判断最高位是否为 1,毕竟浮点数也不需要考虑溢出等等情况,所以用偏量表示更简单也更直接。
情况 3 表示的是特殊情况,比如当数值超出表示范围时的无穷,还有遇到不可计算的情况的 NaN,这个好理解,可为什么还要搞出个情况 2,直接情况 1 不就好了吗? 增加一个情况 2 的目的有两个,一个目的是为了表示 0,另外一个目的是表示 0 附近的数。不知道你有没有发现,情况 1 中的 $M$ 的取值范围限定了该情况下无法表示 0,$M$ 小数点前面的一位并不由 M 部分的 bit 决定,它其实是由 $E$ 部分的情况来决定的,在情况 1 中,这一位是 1,在情况 2 中,这一位就是 0,这样 $M$ 就多了一位可以用来表示尾数,也就提升了可表示的精度。
基于上面的标准,浮点数的二进制表示有挺多有意思的点(假设浮点数有 $k$ 个 bit 的指数位,$n$ 个 bit 的尾数位):
- 作用于无符号整数的排序机制(直接比较二进制流大小)放到浮点数上也同样适用,当然一个排序集合中必须是同一类型的浮点数
- 浮点数中存在
+0.0和-0.0,也就是符号位的差别,虽然二者在数值上一样,但是底层的二进制流并不一样 - 当浮点数二进制最低位为 1,其余位为 0,表示的是 最小的正数,值为 $V=(-1)^0 * 2^{-n} * 2^{-2^{k-1} + 2}=2^{-n-2^{k-1}+2}$
- 当浮点数指数位的最低位为 0,其余位为 1,表示的是 最大的正数,值为 $V = (-1)^0 * (2 - 2^{-n}) * 2^{2^{k-1}-1} = (1 - 2^{-n-1}) * 2^{2^{k-1}}$
- 当浮点数指数位的最高位为 1,其余位为 0,表示的是
1.0
看了上面这些例子,是不是对浮点数的了解又更进了一步呢?
浮点数的精度
用二进制来表示浮点数多多少少会有误差,就比如类似 1/3 这种无限循环小数,我们只能近似表示。还有就是,不管是单精度,还是双精度,因为二进制流能表示的情况有限,所以最终能表示的浮点数个数也是有限的,而实际的浮点数有无限个,因此,很多时候,对于一个实际存在的浮点数,我们只能保证在误差尽量小的前提下近似地去表示它,这里就出现了一个问题,如何做近似?
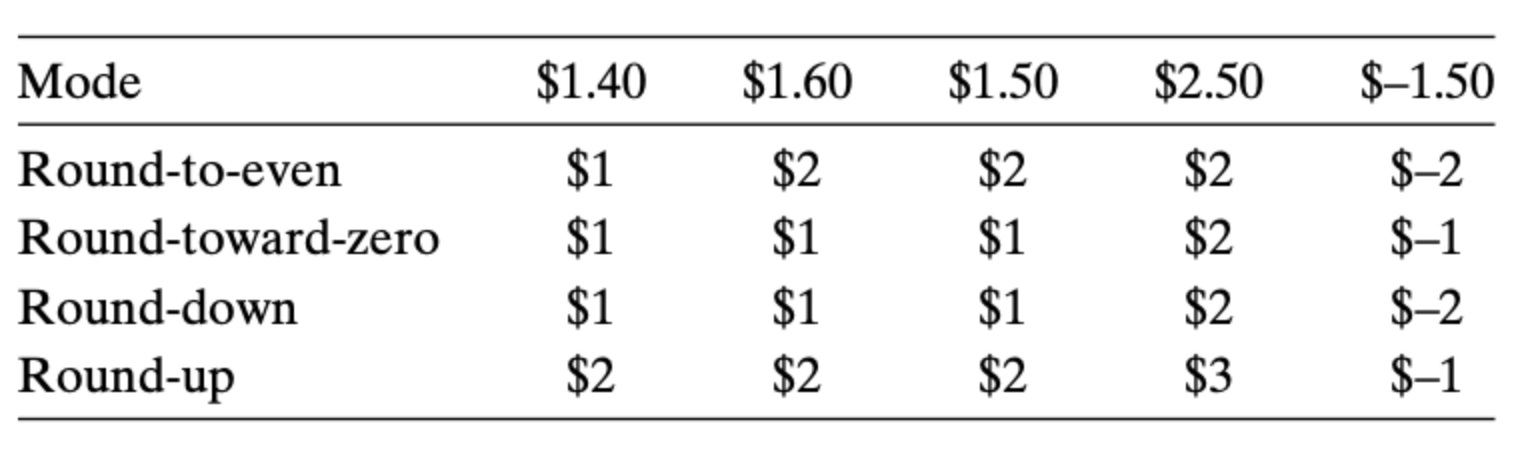
IEEE 给浮点数定义了 4 中近似的模式,默认的模式是向最近的偶数近似(round-to-even):
很多人会有一个疑问,为什么是偶数?这四种模式中,为什么向最近的偶数近似是比较好的模式?
从统计学上来看,其他几种模式都会对统计数据造成比较大的误差,就比如给定一组数据,拿这组数据的实际平均值跟近似后的平均值的差值作为衡量标准,你会发现 round-to-even 所带来的误差最小。因为总的来说,在这种模式下,50% 的情况会向下取整,50% 的情况会向上取整,并且向上和向下的情况一一穿插,分布均匀。因此,大多数情况最近的偶数近似(round-to-even)都是作为浮点数近似的标准模式。
近似往往会隐藏在浮点数的计算中,假设 ƒ 是一个浮点数运算符(比如 +,-,*,/),当计算机计算 x ƒ y 时,其实真实的情况是 Round(x ƒ y),也就是说每次运算都会被近似。这个特性很容易造成计算出的结果不是我们想要的,比如下面这些例子:
- $(3.14+10^100)-10^100$ 最后的结果是 $0.0$,而 $3.14+(10^100-10^100)$ 就可以给出正确的结果 $3.14$
- $10^{200}10^{200}10^{-200}$ 的结果是 ∞,而 $10^{200}(10^{200}10^{-200})$ 给出正确的结果 $10^{200}$
- $10^{200}10^{200}-10^{200}10^{200}$ 的结果是 NaN,而 $10^{200}*(10^{200}-10^{200})$ 给出正确的结果 $0$
上面这些陷阱是我们在用浮点数进行计算时需要考虑到的。
类型转换
我们说了计算机中的整数,也说了浮点数,很多时候我们需要将一个类型转为其他的类型,这里有什么需要注意的呢?
作为举例,我们拿 int,float 以及 double 三种类型之间的转换来进行说明
- 从
int到float,因为编码的关系,数据不会溢出,但是float表示的精度有限,如果是很大的数的话,有可能会被近似 - 从
int或float到double,因为double所表示的范围和精度都足够大,因此不存在溢出,也不存在精度的丢失 - 从
double到float,很明显,同样的编码方式,但是存储空间的限制,存在溢出和精度丢失的风险 - 从
double或float到int,数据会被近似到整数位,同时存在溢出的风险- 当找不到对应的值,或是浮点数的特殊值(Infinity 和 NaN)出现,都会转成 2 的补码下的最小值($-2^{w-1}$,在
int中对应的值是 -214836848)表示 - 把一个很大的浮点数转为整数是计算机中经常出现的一种错误,需要尽量避免
- 当找不到对应的值,或是浮点数的特殊值(Infinity 和 NaN)出现,都会转成 2 的补码下的最小值($-2^{w-1}$,在