经典算法题：找出二维平面中距离最近的两个点

题目介绍

给定一个二维平面，上面有若干个点，算出距离最近的两个点的距离，可以有重合（相同）的点，这样的话两个点的距离为 0。

首先，我们先不着急着解题，先把需要定义的定义清楚，这样才有解题方向。

因为是二维平面，所以对于任意一个点 $ p_1 $，可以表示成 $ p_1 = (x_1,y_1) $，这样的话我们就可以借助 欧几里得距离 公式来计算两点间的距离。比如 $ p_1 = (x_1,y_1) $ 与 $ p_2 = (x_2,y_2) $ 之间的距离就是 $ \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2} $。

暴力解法

通常一开始，我们可以先试着求解，而暂时不去思考优化的事情。一般来说，最直接的方法就是枚举所有可能的情况。对于这道题来说，我们已经知道了所有点，以及它们对应的坐标，我们可以找出所有两两配对的情况 $ (p_i,p_j) $ 其中 $ i != j $，然后求出所有可能的配对的欧几里得距离，选出最小的配对即可。伪代码如下

min = MAX_VALUE;
for( i = 0; i < allPoints.length; i++ )
  for( j = i + 1; j < allPoints.length; j++ )
    if (min > dist(pi,pj))
      min = dist(pi,pj)

假设平面上有 N 个点，那么就会有 $ N(N-1)/2 $ 个配对情况，时间复杂度为 $ O(N^2) $。

暴力解法是可行的，但有没有时间复杂度更低的算法呢？

分治

上面的暴力解法的时间复杂度为 $ O(N^2) $，而想要确定距离最短的配对，遍历所有的点是必须的，所以理性地推测，这个时间复杂度不可能低于 $ O(N) $，而配对不仅仅是简单的遍历就完事了，所以优化后的复杂度大概率是 $ O(NlogN) $。

那这个复杂度又让你想到什么呢？很自然地可以想到排序，但是这里的难点是，我们只能对一个维度的东西进行排序，而这里的点是有两个维度的，排序一个维度后这道题依然没有很清晰的思路。

这里我们可以试着用实现排序的方式来思考，前面我们介绍了 归并排序 以及 快速排序，这两个排序算法的核心都是分治，区别无非是如何分，如何治。那分治的思想用在这里是否合适呢？

分治的第一步就是 “分”，首先从整体看，二维平面可以平行于 Y 轴一刀下去分成两个平面，然后这两个平面又可以再继续分成四个平面，四个平面再继续分成八个，以此类推。直到不能再分（一个平面中仅仅剩下两个点）即可。排序算法也是干了这个事，这里只不过把数组换成了平面，道理是一样的。

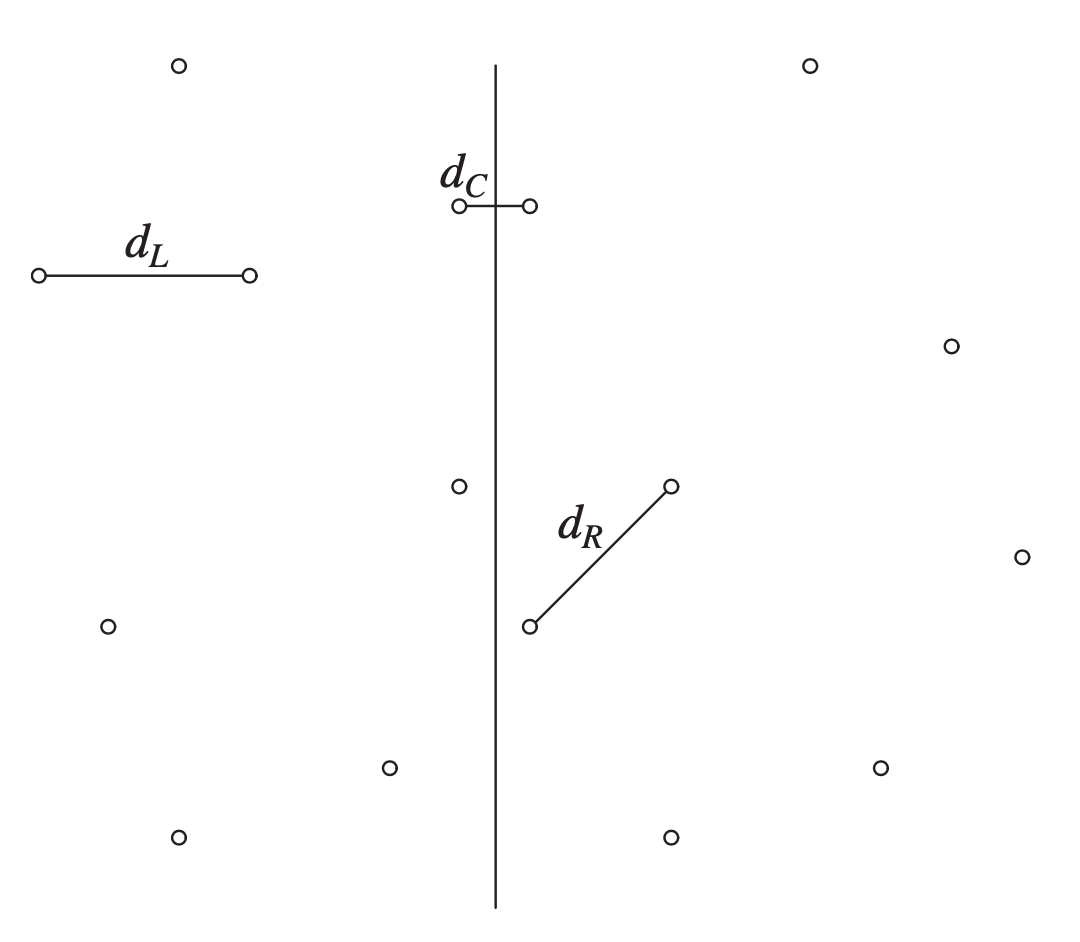
剩下的就是 “治” 与最后的 “合”，因为分到最后一个平面仅剩下两个点，所以答案直接可以计算出来，但是问题是一个平面中的点还可以与旁边平面的点配对，并且这个配对也有可能是最小。所以，在合的时候，我们还需要跨平面考虑。如下图所示

当我们对两个平面进行合并的时候，有 3 个情况要考虑：

1. 两个平面合并后，距离最短的两个点（$ d_L $）都在左平面
2. 两个平面合并后，距离最短的两个点（$ d_R $）都在右平面
3. 两个平面合并后，距离最短的两个点（$ d_C $），一个在左平面，一个在右平面

对于 1 和 2，其实在合并之前我们就已经知道了，现在的问题是如何解决第三种情况？

一开始我们提到，我们希望能将时间复杂度优化至 $ O(NlogN) $，而从之前的排序算法也可以看到，合的这一步的时间复杂度是 $ O(N) $，那么计算 $ d_C $ 肯定就不能用之前的暴力解法，我们需要好好利用已得的条件，也就是这里的 $ d_L $ 与 $ d_R $。

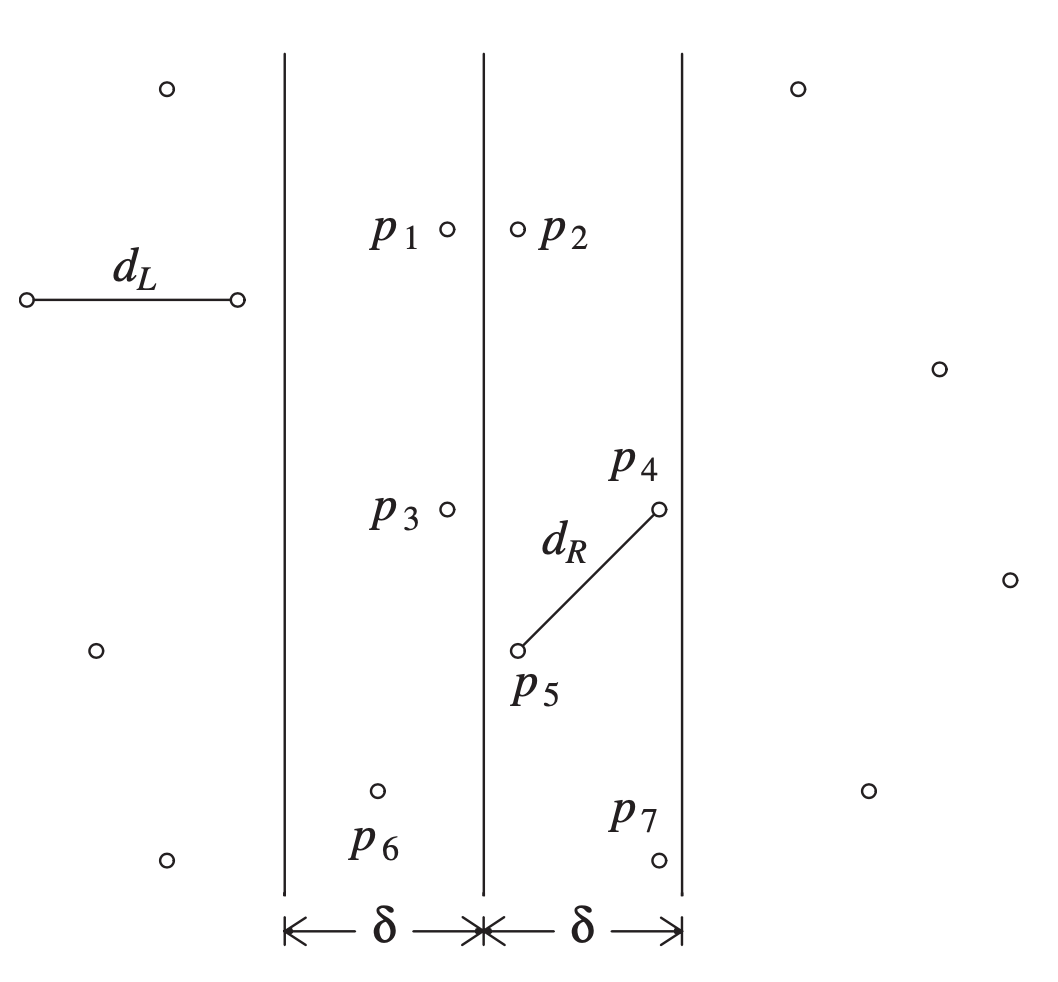
很明显，知道了 $ d_L $ 与 $ d_R $，求解 $ d_C $ 时，我们就可以缩小配对的范围。因为这里我们求的是最小，因而我们只需要考虑比 $ min(d_L,d_R) $ 小的情况，假设 $ δ = min(d_L,d_R) $，我们就可以把 $ d_C $ 的求解范围缩小到 $ 2δ $ 这个小区间内，如下图所示：

如果这个时候在这个小区间内进行暴力求解，枚举所有情况的话，速度会比之前快不少。可问题是，从（最差）时间复杂度来考虑，这个优化依然不到位，因为总是会有特殊情况，导致大部分的点都被框进小区间，最差时间复杂度依旧是 $ O(N^2) $。所以我们还是得继续优化。

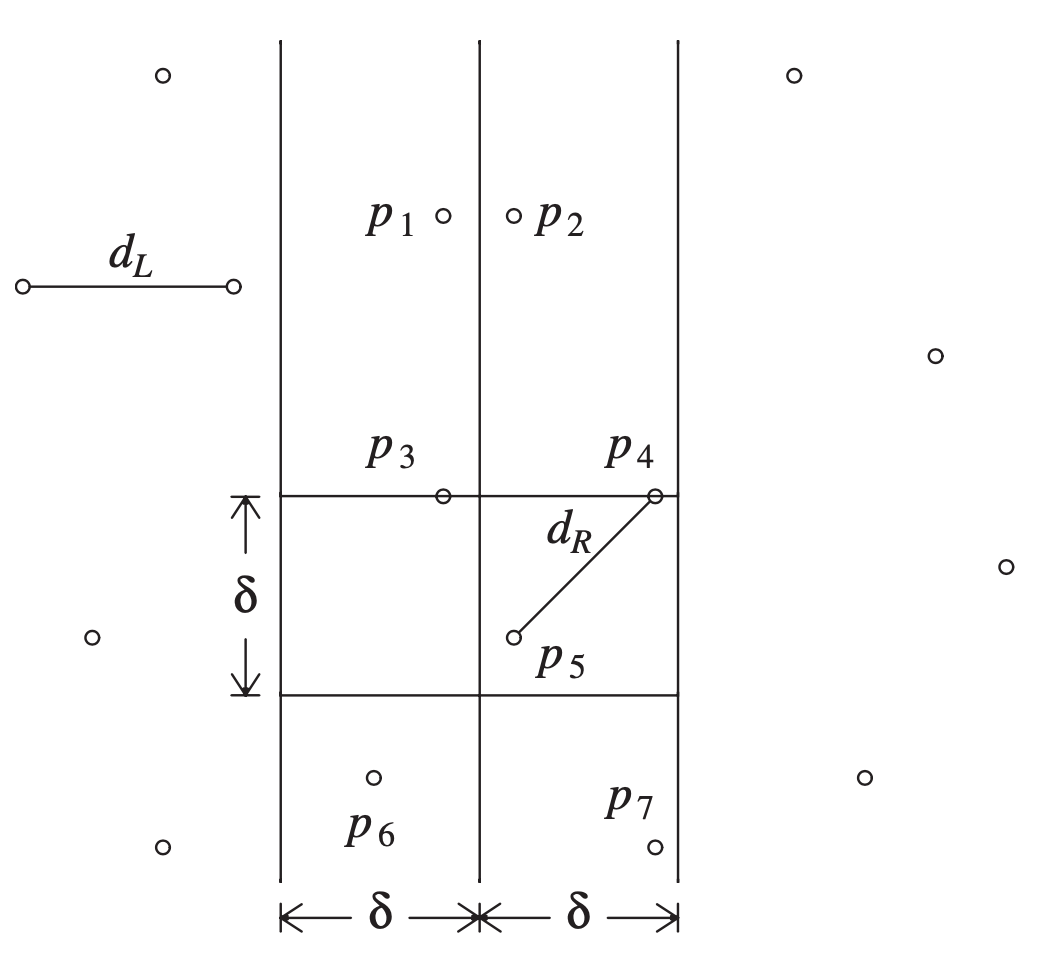
有一个点是，前面将区间缩小到 $ 2δ $ 这个狭长的小区域，我们仅仅考虑了 X 轴，并没有考虑 Y 轴，那么我们能否对 Y 轴做同样的事情呢？答案是肯定的，因为 $ δ $ 限定的是（欧几里得）距离，所以当我们在对任意一点进行配对时，如果对面平面的点在 Y 轴上与之差距过大，我们可以直接排除，无需计算，所以我们可以继续去缩小这个查找范围：

由上图可见，在找一个点的配对点时，我们将配对范围缩小到了一个长为 $ 2δ $，宽为 $ δ $ 的长方体，那优化到这里是否足够了呢？答案也是肯定的。这里我们可以试着分析一下最坏情况，也就是这个区间内最多可能有多少个点。

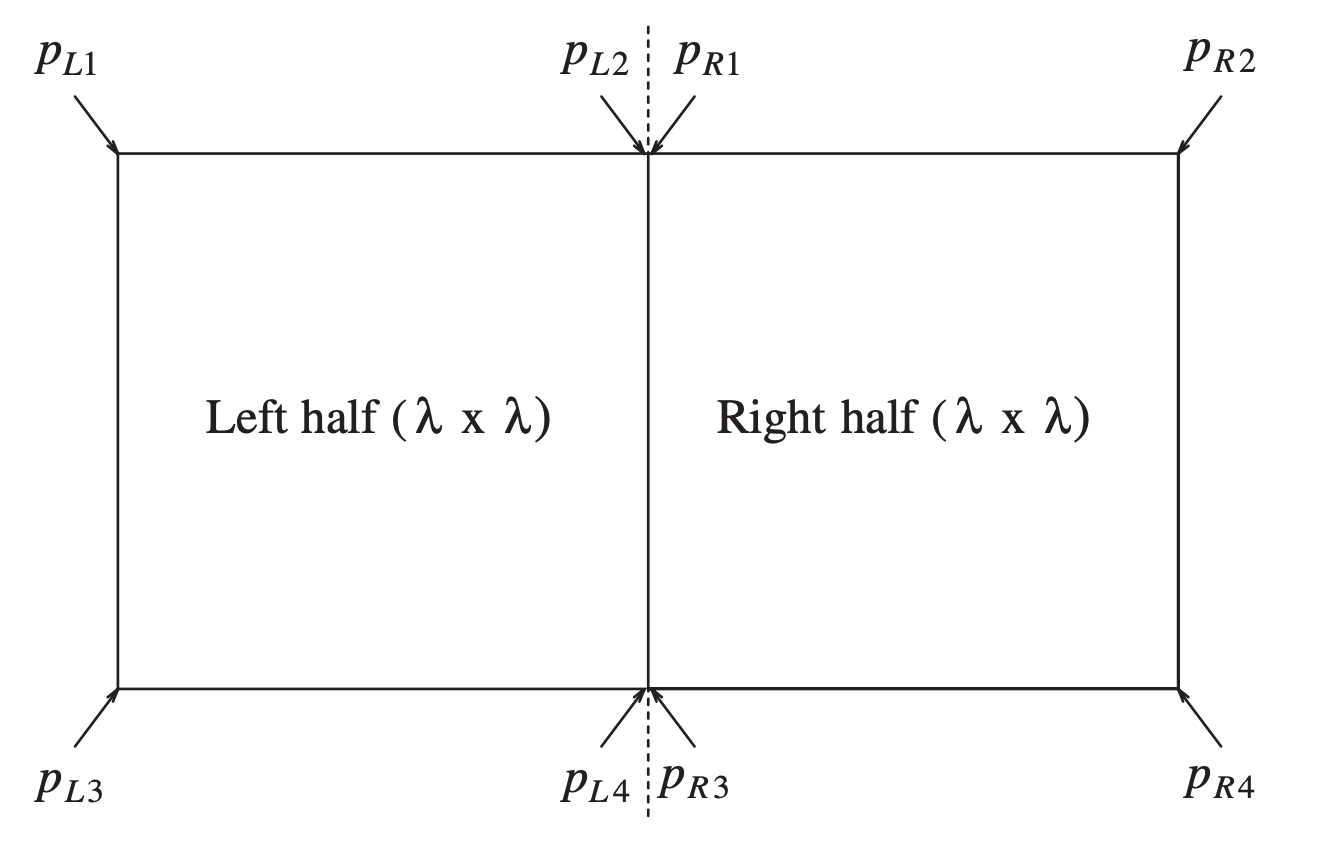
我们把这个长方形一分为二，分成左右两个边长为 $ δ $ 的正方形，左边的正方形属于左平面，右边的正方形属于右平面。仅单独考虑每个正方形的话，因为这是在一个平面内的，所以其中的点的配对距离必然是等于或者大于 $ δ $ 的，也就是说一个正方形中最多存在四个点，这四个点分散在四角，两个正方形的话就是八个点，如下图所示（可以把这里的 $ λ $ 看成是 $ δ $）：

也就是说在 $ 2δ $ 这个狭长区域的任意一点 $ p_i $ 进行配对时，最差的情况都仅需要考虑有限个可能的点，因而这部分的计算时间是 $ O(1) $，所以计算 $ d_C $ 的时间也就是 $ O(N) $。

把 “合” 这部分的逻辑用伪代码写出来就是如下的形式：

for( i = 0; i < numPointsInStrip; i++ )
  for( j = i + 1; j < numPointsInStrip; j++ )
    if( pi and pj’s y-coordinates differ by more than δ )
      break;
    else if( dist(pi, pj) < δ )
      δ = dist(pi, pj);

另外，整个算法在实现上，还有一些具体的细节。因为输入的点是无序排列的，而我们需要将这些点均匀地一分为二，所以在进行分治前，需要将数据先基于 X 坐标排序一遍。排序算法的复杂度为 $ O(NlogN) $，所以这个预处理也不会增加整个算法的时间复杂度。

但是仅有这个预处理还不够，在合的时候我们还对点的 Y 坐标进行了考量和筛选，所以我们还得做另一个预处理，就是把所有的点基于 Y 坐标排一遍，这样我们就有两个序列，一个是基于 X 排完的结果，另一个是基于 Y 排完的结果。在每次分的时候，分割线由基于 X 排序的序列确定，并将 X 序列等量一分为二，在此之后，我们可以用 $ O(N) $ 的时间遍历一遍基于 Y 排列好的序列，然后对照着分割线的 X，生成左右两个排序好的 Y 序列。这些操作均不会影响最终的时间复杂度。同理，在合的过程中，当 $ 2δ $ 的狭长区域确定后，我们依旧可以通过 $ O(N) $ 时间遍历 Y 序列并仅选出在区域内的点，选出来的这些点依旧是排好序的。

加上上述细节，整个算法的时间复杂度就被优化成了 $ O(NlogN) $。