红黑树：最常用的平衡二叉树

红黑树原理介绍

红黑树这个名字，想必很多人都不陌生，但是真正了解的人少之又少，主要可能是因为红黑树里面的逻辑并不像动态规划、搜索这么实用。我们经常调侃，说如果红黑树被选为一个公司的面试题，那么这个公司大概率不想招人。但不管怎样，我们都无法否定红黑树的价值，你虽然不了解它，但肯定直接或间接地使用到它，比如说 Java（Java 1.8 往后） 中的 Hash 就是利用红黑树来存储发生 Hash 冲突的元素。那么今天我们就来打开这个黑盒子，看看红黑树究竟是一个什么样的结构。

再说红黑树之前，我们还是要搬出之前说过的 AVL 树。AVL 树与红黑树均为平衡二叉搜索树，且各项操作的时间复杂度都一样。但是相比于 AVL 树，红黑树会更加地稳定，这个稳定体现在运行效率以及实现上，这个我们后面会提到。红黑树在操作上会用到 AVL 树中的旋转，之前在说 AVL 时也提到过，这些旋转可以维持树的平衡，让操作的时间复杂度不会退化。

关于具体的操作，我们先放一放，先来看看红黑树的 4 个特性：

1. 每个树节点都会被标记为红色或者黑色
2. 根节点必须为黑色
3. 如果一个节点为红色，那么它的子节点必须为黑色
4. 从一个节点到空节点（null）的所有路径必须含有相同数量的黑色节点

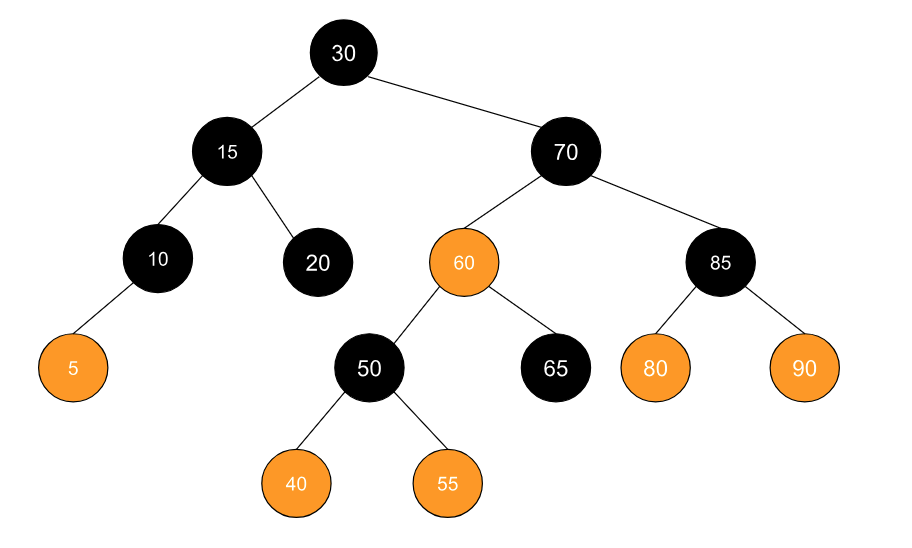
我们暂且不必纠结为什么会有这些特性，这是红黑树正常运作的前提，在任何的操作下，红黑树都需要维持这些特性。前两个特性其实好说，关键是后面两个。和 AVL 树一样，红黑树的结构改变是因为树节点的插入和删除。让我们通过实例来看看，比如有如下这个红黑树：

试想一下，当我们往红黑树里面插入元素时，依照二叉搜索树的特性，元素会被插入到某个节点下。如果说这个节点是黑色的，那么很好办，直接将这个新插入的节点设定为红色的即可。比如插入 25 这个元素。但麻烦的是，如果这个节点是红色的呢？比如当我们插入 3 或者 6，这两个节点最终都会落到节点 5 的下面，而节点 5 是红色的，如果我们把新节点标记为红色的，这显然违背了第 3 个特性，但是如果我们把新节点标记为黑色的，这虽说不违背第 3 个特性，但是违背了第 4 个特性，在这种情况下，我们就需要做调整。怎么调整？旋转以及改变颜色。

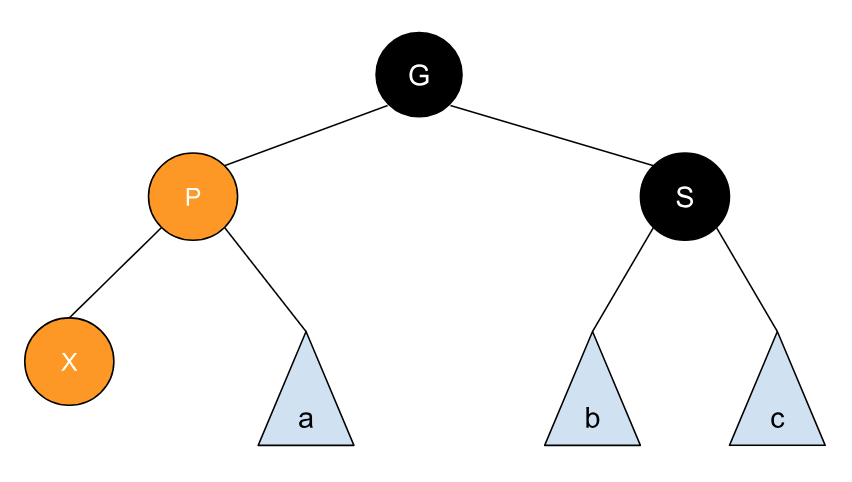
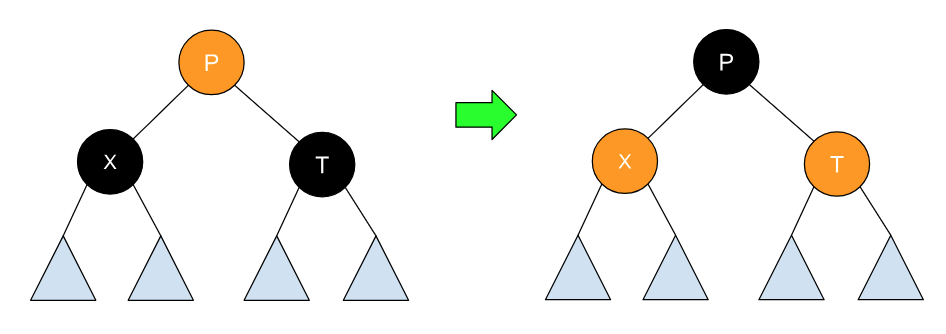
也是和 AVL 树类似，我们得具体情况具体分析，假设新插入的节点为 X，它的父节点为 P，祖父节点为 G，父节点的兄弟节点为 S，如下图所示：

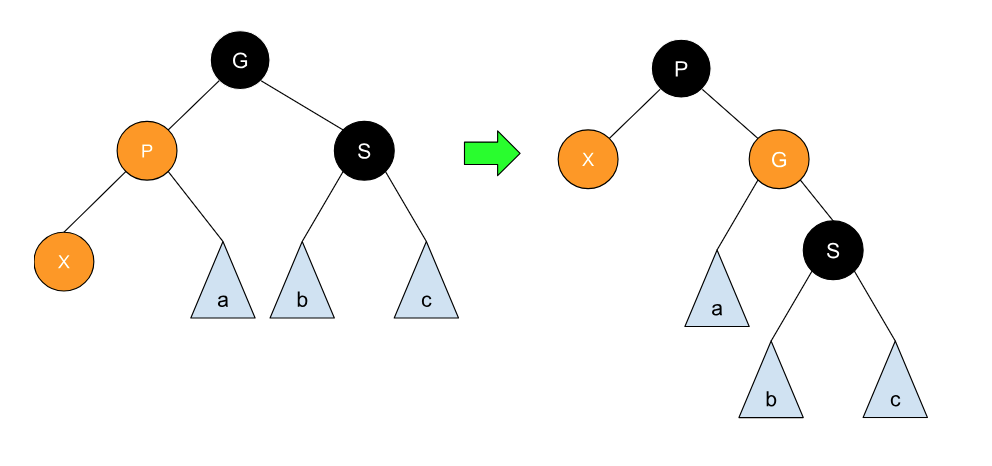
在这种情况下，我们可以沿用 AVL 中的单次旋转（通过交换 P 与 G 的位置与颜色），来改变这部分的结构，如下图所示：

旋转之后的这部分树结构就没有违反特性 3 与 4，类似的，这种情况还有一个对称情况，无非是把 P 与 S 的位置对调一下，然后 X 出现在 P 的右节点处，可以参考之前的 AVL 树的文章，这里就不过多赘述。

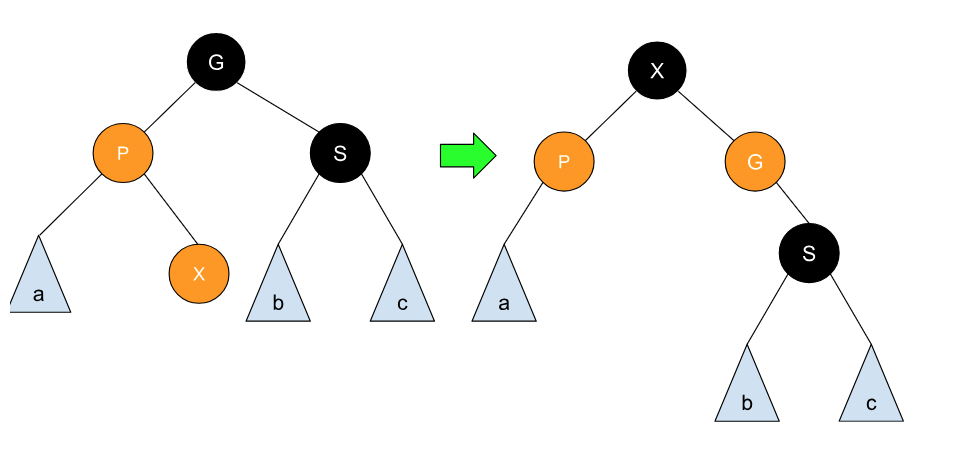
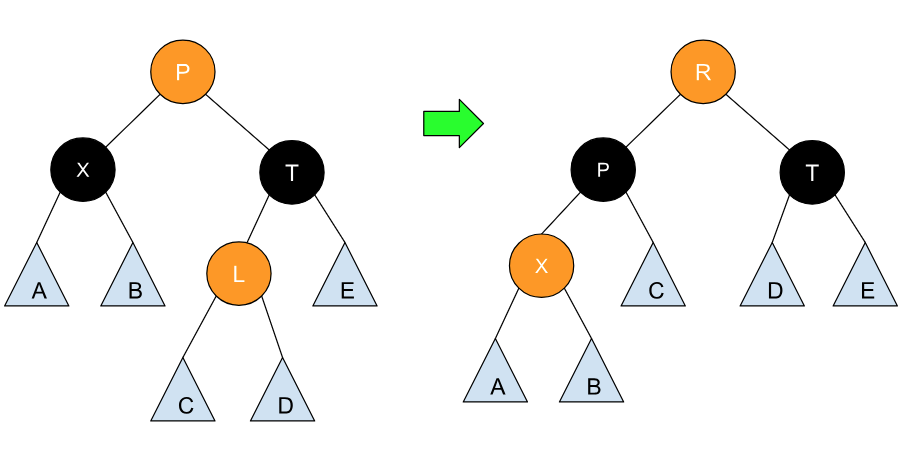
另外一种较为复杂的情况是 X 出现在 P 的右节点处，这时就可以使用两次旋转，第一次旋转交换 P 与 X 的位置，第二次旋转交换 X 与 G 的位置和颜色：

同样，交换完后，这部分树结构依旧满足红黑树的 4 个特性。这个也是有另一种对称情况。

如果你仔细看，就会发现这两种情况的 S 都是黑色的，如果 S 为红色的话呢？比如我们往前面的红黑树中插入 79 这个元素。这种时候，旋转过后虽然 X 不会破坏红黑树的特性，但是 G 与 S 同为红色，违背了第 3 个特性。我们还剩下改变颜色这一条路，可以把这部分结构的根节点由原来的黑色变成红色，然后根节点下面的两个节点变为黑色，这样这个结构就依然满足红黑树的 4 个特性，你可以对照着上面的旋转后的情况想想看是不是这样。

虽然说这部分结构没有违背特性，但是这也只是树的一部分，如果这部分的根节点原来的父节点也恰巧是红色的呢？那就继续向上改变颜色，类似于 G 与 S，最不幸的情况是，最终整棵树的根节点被改成了红色，这虽说违背了原则 2，但解决办法其实很简单，就是直接将根节点再改回黑色，这并不会破坏任何一个特性。

到此为止，我们就基本了解了红黑树的基本特性以及维持平衡的方式方法。

从上到下的实现思路

对于红黑树来说，原理是一回事，实现又是另一回事。照着原理实现你会发现，这里面有各种的临界情况，比如说如何判断空，如何判断遍历到头，如何区别对待根节点等等。按照我们之前的思路，旋转完后，我们需要借助递归，向上去更新节点的颜色，如果不使用递归，我们则需要在每个节点中维护一个指向父节点的指针，这都增加了实现的难度。

这里我们尝试着换一种思考问题的角度，我们从上往下来遍历并更新树结构，类似于之前讲过的 Splay 树的实现。

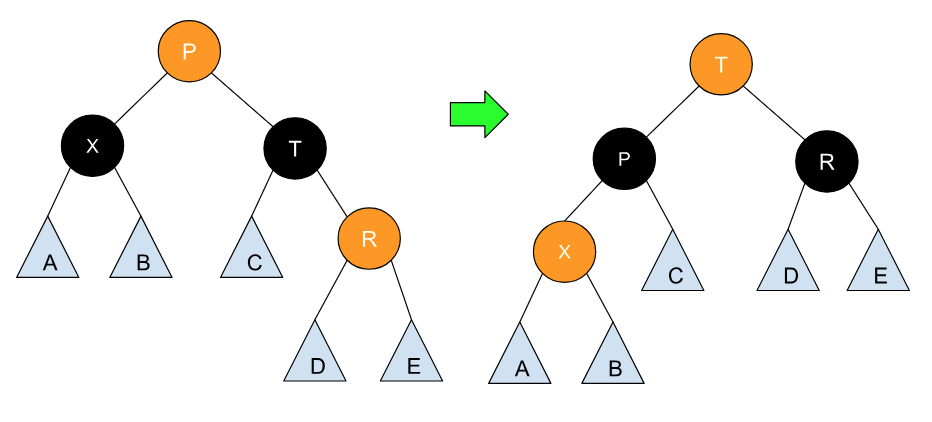
当我们得知需要定位的元素后，在从上到下搜索的过程中，每到一个节点，我们只需要做一个判断，那就是这个节点是否为黑色，并且有两个红色的子节点（空节点是黑色），如果是这种情况，那么我们就做一个颜色上移的操作（如下图所示）：

操作过后，如果祖父节点（P 的父节点）也为红色，那我们就可以执行提到过的旋转操作来交换节点 P 与其祖父节点的层级位置。这里有一个疑问就是有没有可能，P 的兄弟节点也是红色的？这样的话，旋转过后的树依然是违背红黑树特性的。其实这种情况已经被排除了，因为我们是从上到下遍历，如果存在这种情况，在祖父节点的父节点处我们就会执行颜色上移的操作。

不但 P 的兄弟节点不可能是红色的，节点 A 和 B 的子节点也都不可能是红色的，因为这在操作前就违背了第 3 个特性。因此，旋转过后的树结构是肯定不会违背红黑树特性的。

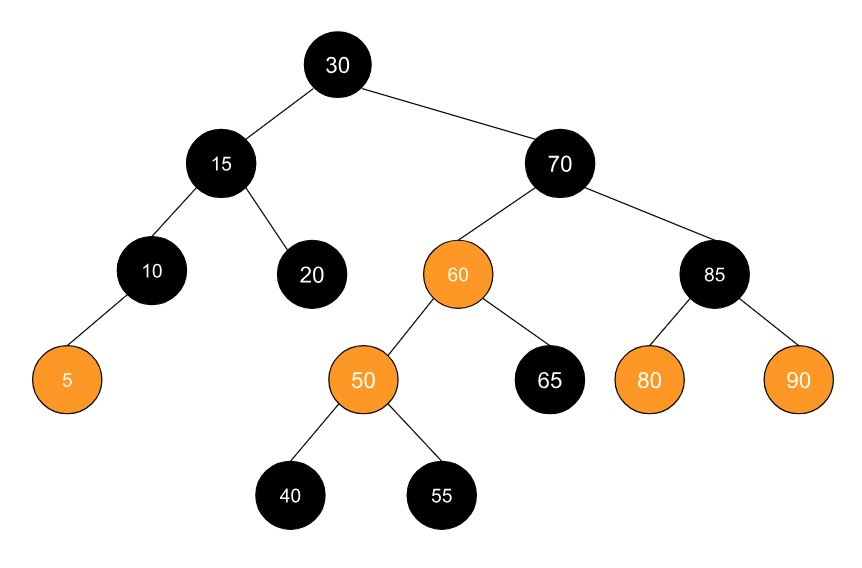
让我们通过实例来梳理一下，回到一开始的例子：

假设此时我们需要插入一个元素 46，我们依照二叉搜索树的特性向下遍历，直到节点 50 处，我们判断到了需要颜色上移的操作，于是执行这个操作，操作后树如下图所示：

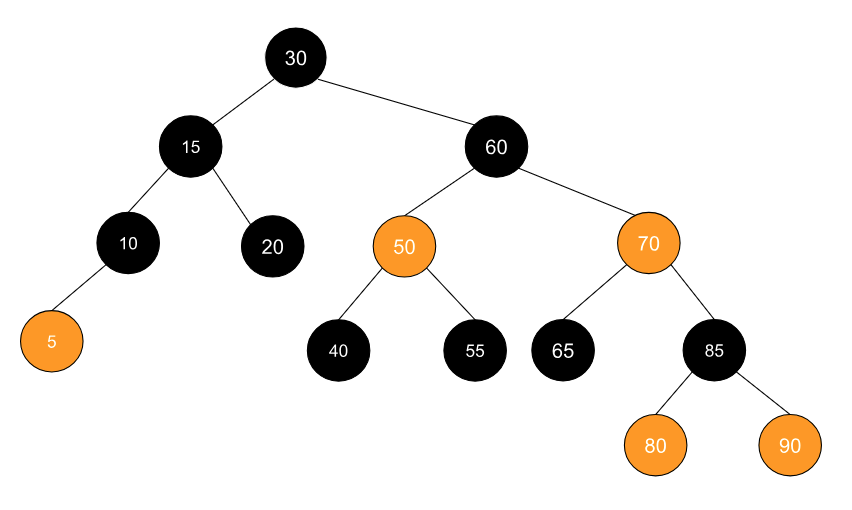
可是，这时显然没完，节点 50 和节点 60 均为红色，违背了红黑树的特性 3，于是我们执行旋转操作，操作后的树就如下图所示：

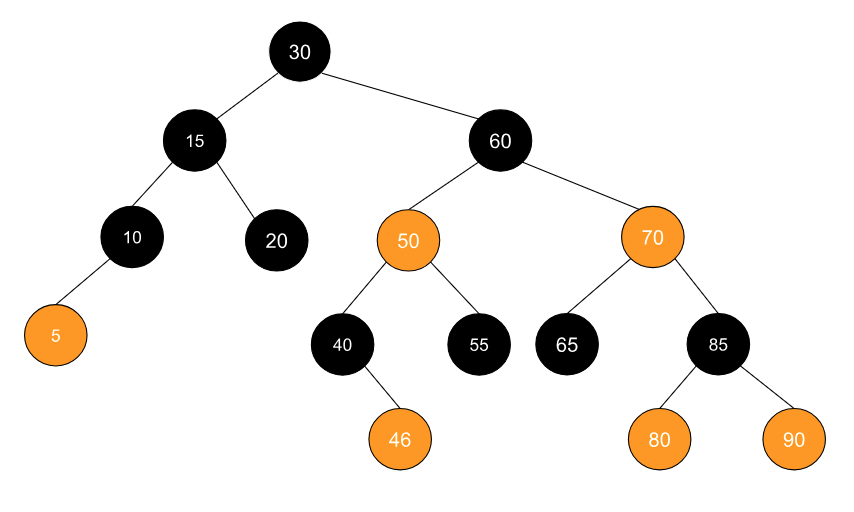
我们从节点 50 处继续向下遍历，直到将节点插入到指定的位置：

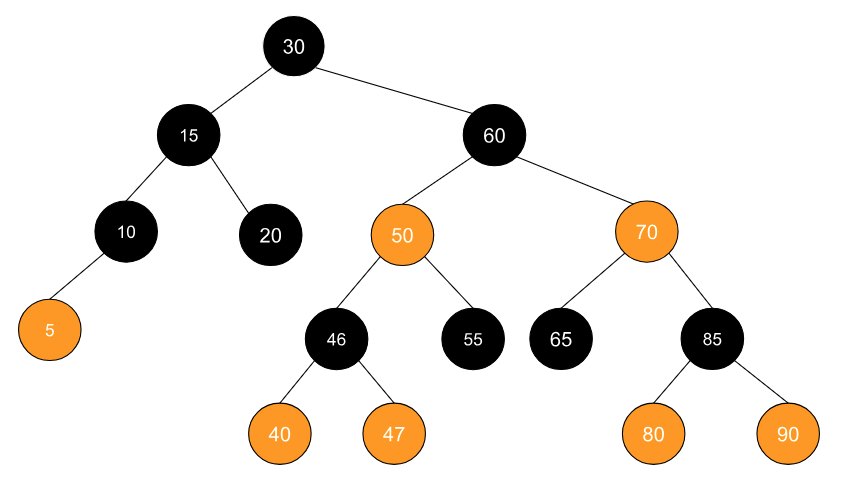
此时，很多人可能会说，那如果我们继续插入 47，这在插入后不久违背原则了吗？这也简单，插入后如果违背特性（插入节点的父节点为红色），直接旋转就好了，继续插入 47 后树就长这样：

从插入后的树结构我们也可以看到，这颗树在两次插入后依然维持着插入前的高度。其实，实际情况表明红黑树有着 AVL 树的平均高度，并且操作所需要的常数级时间复杂度更少，而且旋转的频率也相对更低。

具体实现

插入

依照我们前面将的思路来实现，我们不需要使用递归，从上到下遍历就好，但这里有几个细节需要指出:

1. 在遍历的过程中我们需要保留 4 个节点的引用，分别是当前节点，当前节点的父节点、祖父节点、以及曾祖父节点。至于原因，可以回去看看旋转操作，并思考需要更改的节点有哪些。
2. 我们维护一个全局的空节点，这个节点起到哨兵节点的作用，省去了代码中的很多额外操作，降低了代码的复杂度。
3. 在旋转过后虽然 1 中的 4 个引用存放的节点会发生变化，但是继续遍历直到下一次旋转发生，我们依然可以保证这些引用的正确性（可以对照着之前的实例图思考下）。

于是我们可以得到下面的代码，具体的明细都在注释中。

public class RedBlackTree<AnyType extends Comparable<? super AnyType>> {

  // header 和 nullNode 均为哨兵节点，起辅佐作用
  private RedBlackNode<AnyType> header;
  private RedBlackNode<AnyType> nullNode;

  private static final int BLACK = 1;
  private static final int RED   = 0;

  public RedBlackTree() {
    nullNode = new RedBlackNode<>(null);
    nullNode.left = nullNode.right = nullNode;
    header = new RedBlackNode<>(null);
    header.left = header.right = nullNode;
  }

  private static class RedBlackNode<AnyType> {
    AnyType element;
    RedBlackNode<AnyType> left;
    RedBlackNode<AnyType> right;
    int color;

    RedBlackNode(AnyType theElement) {
      this(theElement, null, null);
    }

    RedBlackNode( AnyType theElement, RedBlackNode<AnyType> lt, RedBlackNode<AnyType> rt ) {
      element = theElement; left = lt; right = rt; color = RedBlackTree.BLACK;
    }
  }

  private RedBlackNode<AnyType> current;
  private RedBlackNode<AnyType> parent;
  private RedBlackNode<AnyType> grand;
  private RedBlackNode<AnyType> great;

  public void insert(AnyType item) {
    current = parent = grand = header;

    // 我们将需要插入的元素放到空节点上
    // 这样定位找到空节点了就说明元素不存在，需要插入
    // 否则，表明元素已存在，直接跳过，不做插入
    nullNode.element = item;
    while(compare(item, current) != 0) {
      // 在移动当前指针前，更新父辈节点的引用
      great = grand; grand = parent; parent = current;
      current = compare(item, current) < 0 ? current.left : current.right;

      // 如果当前节点下有两个红色的子节点，进行颜色上移，如有需要进行旋转
      if(current.left.color == RED && current.right.color == RED) {
        handleReorient(item);
      }
    }

    // 元素已存在，直接跳过，不做插入
    if(current != nullNode) {
      return;
    }

    // 创建新节点，并作为叶子节点插入
    current = new RedBlackNode<>(item, nullNode, nullNode);
    if( compare(item, parent) < 0 ) {
      parent.left = current;
    } else {
      parent.right = current;
    }

    // 将新插入的节点变为红色，这样就不违背特性 4
    // 如果父节点也为红色，进行旋转操作
    handleReorient(item);
  }

  // handleReorient 会进行颜色上移
  // 如有需要则会进行旋转操作
  private void handleReorient(AnyType item) {
    // 颜色上移
    current.color = RED;
    current.left.color = BLACK;
    current.right.color = BLACK;

    // 如果父节点也为红色，则表明需要进行旋转
    if(parent.color == RED) {
      grand.color = RED;

      // 当前节点的位置处在中间时，需要双旋转
      if( (compare(item, grand) < 0) !=
          (compare(item, parent) < 0) ) {
        parent = rotate(item, grand);
      }

      current = rotate(item, great);
      current.color = BLACK;
    }

    header.right.color = BLACK;
  }

  private RedBlackNode<AnyType> rotate( AnyType item, RedBlackNode<AnyType> parent ) {
    if (compare(item, parent) < 0) {
      return parent.left = compare(item, parent.left) < 0 ?
        rotateWithLeftChild(parent.left)  :  // LL
        rotateWithRightChild(parent.left) ;  // LR
    } else {
      return parent.right = compare(item, parent.right) < 0 ?
        rotateWithLeftChild(parent.right) :  // RL
        rotateWithRightChild(parent.right);  // RR
    }
  }

  private RedBlackNode<AnyType> rotateWithLeftChild(RedBlackNode<AnyType> t) {
    RedBlackNode<AnyType> tl = t.left;
    t.left = tl.right;
    tl.right = t;
    return tl;
  }

  private RedBlackNode<AnyType> rotateWithRightChild(RedBlackNode<AnyType> t) {
    RedBlackNode<AnyType> tr = t.right;
    t.right = tr.left;
    tr.left = t;
    return tr;
  }

  private final int compare( AnyType item, RedBlackNode<AnyType> t ) {
    if(t == header) {
      return 1;
    } else {
      return item.compareTo(t.element);
    }
  }
}

删除

有插入就有删除，红黑树的删除其实跟普通二叉搜索树类似，当我们定位到了要删除的节点，我们通常不会直接将原节点删除，而是将原节点与其左子树中最大的元素，或者是右子树中最小的元素进行值的交换，然后去到下面删除交换后的节点。

但是这里还是需要考虑一个问题，当我们删除的节点是红色的，这没有问题，但如果我们删除的节点是黑色的，删除后就会破坏红黑树的特性 4，处理这个问题是删除操作的关键。我们需要确保被删除的节点是红色的，解决办法依然是前面提到过的颜色转换，或是旋转。

这里我们分情况讨论，我们假设当前要删除的节点是 X，其父节点是 P，兄弟节点是 T，第一种情况是 X 的两个子节点都是黑色的（空为黑色），并且兄弟节点的两个子节点也为黑色，这样在父子上做颜色互换即可：

但如果说兄弟节点 T 下面有一个节点是红色的，单纯的颜色互换就行不通了，因为这会违背特性 3，这时我们就需要执行旋转操作：

上面这些情况都是基于 X 有两个黑色的子节点，如果 X 的其中一个子节点是红色的，那么上面的情况就不适用了。这时我们就需要继续遍历，继续去寻找可替换的节点，如果我们在 X 下面找到了一个红色的可替换节点，直接替换后删除就行。反之，如果找的节点依然是黑色的，我么就可以回到上面的例子，根据实际情况进行颜色互换，或是旋转来达到目的。