最短路径问题的另一种思路
问题回顾
在之前的 文章 中我们用 Dijkstra 算法来找出给定点与其余点的最短路径,也简单介绍了图的一些基本概念,有兴趣的话可以看看。
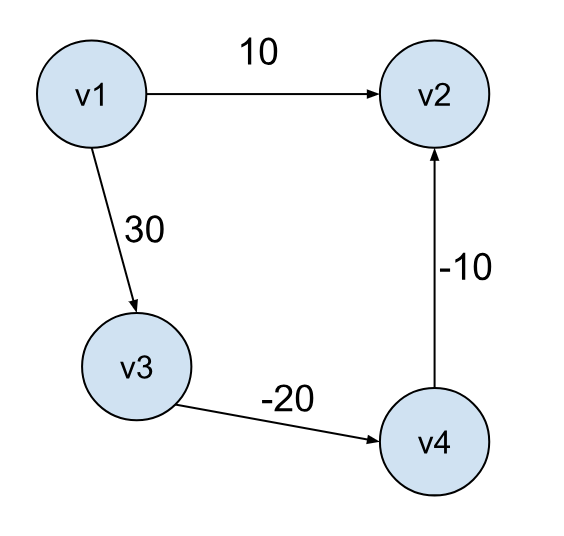
这里需要重点指出,不含有负权重是 Dijkstra 算法成立的必要条件,具体原因在之前的文章中讲过,就不过多赘述。比如下面这个例子,使用 Dijkstra 算法计算出来的答案就是错误的:
那么有没有什么办法能够让我们规避这样的错误呢?如果一直在 Dijkstra 上死磕,肯定是没有结果的,因为 Dijkstra 背后的思想是贪心算法,其特性已经限定了我们只能考虑局部的问题,可在这种情况下,局部没法推导至整体。我们需要另辟蹊径才行。
新的思路
对上面的 Dijkstra 算法的错误案例进行反思后,我们可以看到,最短路径可能存在于两个不直接相连的点之间,比如上面的例子中,v1 到 v2 的路径有两条,分别是 v1 -> v2 以及 v1 -> v3 -> v4 -> v2,而 Dijkstra 仅仅考虑了前者。如果我们可以把后一种情况给考虑进来,那问题岂不是就可以解决了?可这又如何做到呢?
或者这样说,我们是否可以把从 v1 到 v2 的所有可能的情况(路径)都给考虑到。排除暴力枚举后,我们可以很自然地想到用动态规划来求解,用动态规划的第一步是要定义好状态,首先在这个问题中,那么这个问题有三个变量,起点,终点,还有路径。如何将路径放到状态中是一个难点,但是仔细想想,路径也是由点组成的,我们还是可以试着将落脚点放在节点上。
我们定义 $DP_{k,i,j}$ 为节点 $v_i$ 到 $v_j$ 的最短路径,并且这个路径可以经过 $v_0,v_1,…,v_k$ 中任意一个或多个点,注意不一定是必定经过,只是说可以经过。最后 $DP_{V,i,j}$ 就是最终 $v_i$ 到 $v_j$ 的最短路径,$V$ 涵盖了所有的节点。
定义完状态后,我们再来试着想想递推方程,我们可以思考上一步状态和当点状态的关系。假设 $DP_{k,i,j}$ 就是当前状态,上一步仅考虑 $v_0,v_1,…,v_{k-1}$,状态就是 $DP_{k-1,i,j}$。当前步和上一步的不同之处在于,我们引入 $v_k$ 来充当中间节点,这个中间节点就像一个桥梁一样,$v_i$ 可以先到 $v_k$,然后借由 $v_k$ 再到 $v_j$,这样子,递推方程就出来了:
\[DP_{k,i,j} = MIN(DP_{k-1,i,j}, DP_{k-1,i,k} + DP_{k-1,k,j})\]递推方程出来,这个问题基本上就解决了,剩下的就是优化的问题。因为有 3 个变量,那么是不是意味着我们需要用到 3 维数组?如果仔细看递推方程,你会发现 $DP_{k,..}$ 只和 $DP_{k-1,..}$ 有关,因此我们只需二维数组即可,具体实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public static int shortestPath(int[][] graph, int s, int d) {
if (s == d) {
return 0;
}
int n = graph.length;
int[][] dp = new int[n][n];
int[][] path = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j] = graph[i][j];
path[i][j] = -1;
}
}
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (dp[i][k] + dp[k][j] < dp[i][j]) {
dp[i][j] = dp[i][k] + dp[k][j];
path[i][j] = k;
}
}
}
}
int idx = s;
// 打出路径
System.out.print(idx + "->");
while (path[idx][d] != -1) {
System.out.print(path[idx][d] + "->");
idx = path[idx][d];
}
System.out.print(d);
return dp[s][d];
}
这里面,路径打印不是必须的,但是可以帮助我们查看具体的情况,以及 debug 等等。这个时间复杂度是 $O(V^3)$,空间复杂度是 $O(V^2)$,当然了从效率来说,这个算法比不上之前的 Dijkstra,但是这个算法可以允许权重为负的边,这个是 Dijkstra 所不能及的。
算法对比与分析
之所以这个算法的时间复杂度偏高,主要是因为这个算法解决的问题和之前稍有不同,你会发现,我们其实并不单单在求单个点与其他点的最短路径,我们是在求所有点两两之间的最短距离,所有的答案都包含在 dp 数组中,我们把程序改成下面这样可能比较合适:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public static void allPairs(int[][] graph, int[][] dp, int[][] path) {
int n = graph.length;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j] = graph[i][j];
path[i][j] = -1;
}
}
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (dp[i][k] + dp[k][j] < dp[i][j]) {
dp[i][j] = dp[i][k] + dp[k][j];
path[i][j] = k;
}
}
}
}
}
其中,dp[i][j] 表示的就是 $v_i$ 到 $v_j$ 的最短距离,通过对 path 的遍历,我们也可以知道具体路径是什么。
那么试着想想,如果要用 Dijkstra 来求解这个问题,时间复杂度又会是多少呢?其实也是 $O(V^3)$,当然了,我们可以考虑使用优先队列来进行优化,但就实际的运行来说,还是动态规划来得更快,因为基本上就是数组的遍历,几乎没有什么额外操作,比较的次数也相对较少。
贪心算法和动态规划都能用来解决最短路径问题,但是可以看到这两种方式所采取的策略皆然不同。贪心算法单纯是比大小,做取舍拿到局部的最优解,最终算出全局最优。而动态规划的思路更像分治,都是通过对问题拆解,通过求解子问题,并找到子问题之间的关系来得到整个问题的解,只不过二者在问题的拆分和定义上有所不同。
通常来说,动态规划理解起来更加困难,里面牵扯到如何定义状态,又如何通过状态来得到递推方程等等,但是这种解决问题的方式看着非常的舒服,实现起来也比较简单。但是想真正熟练掌握动态规划,只能靠我们平时多看多想,对同样一个问题,可以尝试着用不同的状态来表示,久了,感觉就有了。