文件压缩算法：霍夫曼编码

背景介绍

在介绍这个算法之前，我们先来说说文件压缩与编码到底是怎么一回事。

我们知道计算机是基于二进制的，也就是说任何信息到最后其实都变成了类似 0101101010101... 这样的序列。文件中存储的也是这样的序列。但你会说，不对呀，为什么我打开文件看到的是具体的文字和内容。这就要说到编码了，通过编码，我们使得这样的序列变得有意义了。

比如最常见的 ASCII 编码，就是对一些英文字符以及常用的符号进行编码，比如 a 这个字符，它的二进制表示是 01100001。也就是一个文件，这里面的内容最后都会通过编码转化成二进制序列在计算机上存储。

那么这就有个问题，文件在硬盘上存储是需要硬盘空间的，将文件通过网络传输是需要网络带宽的，把文件加载到内存中也是需要内存空间的。直接将一个大的文件进行网络传输，或是直接存储，都需要耗费大量的空间和时间，那么我们可否通过一定的方式将文件进行压缩来节省资源。当然可以，这就是文件压缩算法做的事情。

编码树

文件压缩要做的事情就是尽量缩小二进制流的长度，但要保证文件信息不失真。为了方便起见，这里我们假设一个文件中只有 a，e，i，s，t，空格，换行这几种编码，它们具体编码，出现的频率，如下：

Character	Code	Frequency	Total Bits
a	000	10	30
e	001	15	45
i	010	12	36
s	011	3	9
t	100	4	12
space	101	13	39
newline	110	1	3
Total			174

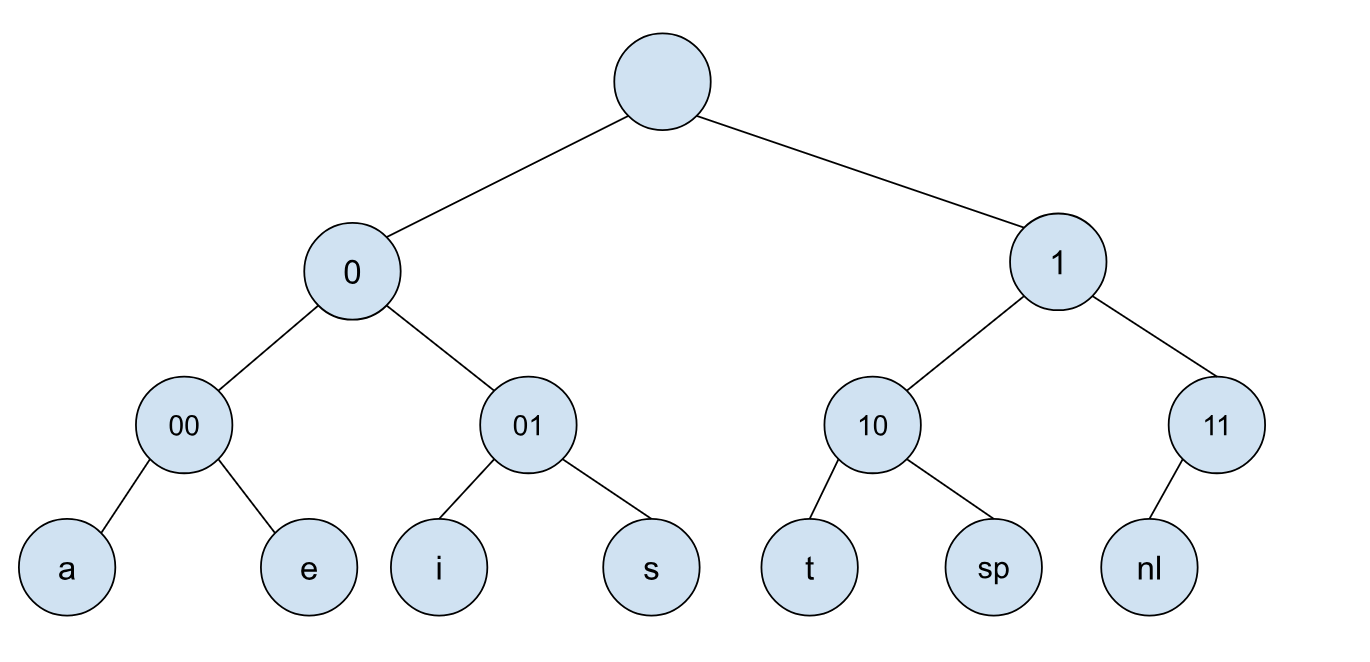
这个文件总共是有 174 个 Bits，如果是不压缩直接传输，那么我们需要传输 174 个 Bits。因为编码里面不是 0 就是 1，我们可以基于此构建一个编码树：

这其实就是一个普通的二叉树，根节点表示的信息为空，往左表示新增一个 0， 往右表示新增一个 1，我们的编码对应的字符均在叶子节点上。

这树跟字典树（Trie）很相似，只不过字典树上的字符变成了 0 或 1。如果想要对文件进行压缩，那么我们势必要在编码上面做文章，那么最终与之相对应的编码树也会改变。

那么这里有哪些地方可以优化呢？首先观察到的一点是，叶子节点的深度决定了该字符对应的长度，所以，对于那些出现频率特别高的字符，我们需要降低其叶子节点的深度。

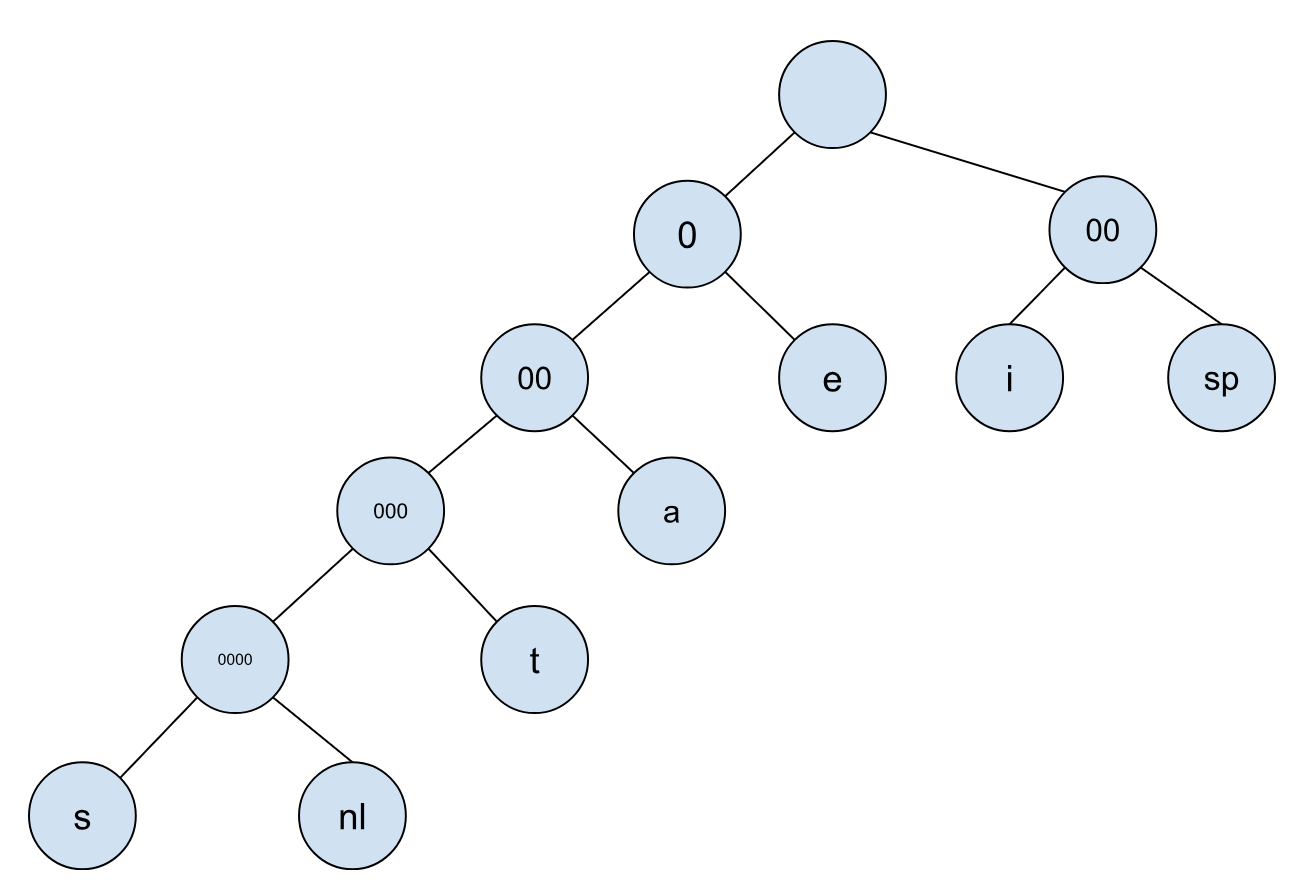
比如下面这颗编码树：

上面这颗编码树所对应的表格如下：

Character	Code	Frequency	Total Bits
a	001	10	30
e	01	15	30
i	10	12	24
s	000000	3	15
t	00001	4	16
space	11	13	26
newline	00001	1	5
Total			146

可以看到基于这组编码后的文件总共只需要传输 146 Bits 的信息，相比于之前的 174 有所提高。

可能很多人会有一个疑问就是，为什么每个字符的编码长度可以不一样？这里需要清楚的是，这里的编码的目的是为了节省空间，它并不是像 ASCII 编码那样需要考虑所有的情况，所有的字符。这里我们仅仅需要考虑已经出现过的字符就好了。

另外，只要我们能够保证所有字符的编码都在叶子节点上，那么最后编码的信息就是唯一确定的。这里面的原理就是，所有字符都没有重叠，一个字符的编码永远不可能是另外一个字符的编码前缀，这样的编码方式也被称为前缀编码（prefix code）。

霍夫曼编码算法就是为了找到最优的编码树，使得总的传输 Bit 最小。

霍夫曼编码

通过观察，我们的一个直观感受是，频率小的字符需要尽可能地安放在深度深的叶子节点，频率大的字符需要尽可能地安放在深度浅的叶子节点。霍夫曼编码是通过树节点的合并来达成的，它选择先合并频率小的节点，最后再合并频率大的节点，这样能保证所有的字符节点都是叶子节点，而且可以保证最后的 Bit 数是最优的。

我们还是以之前的例子来进行说明。

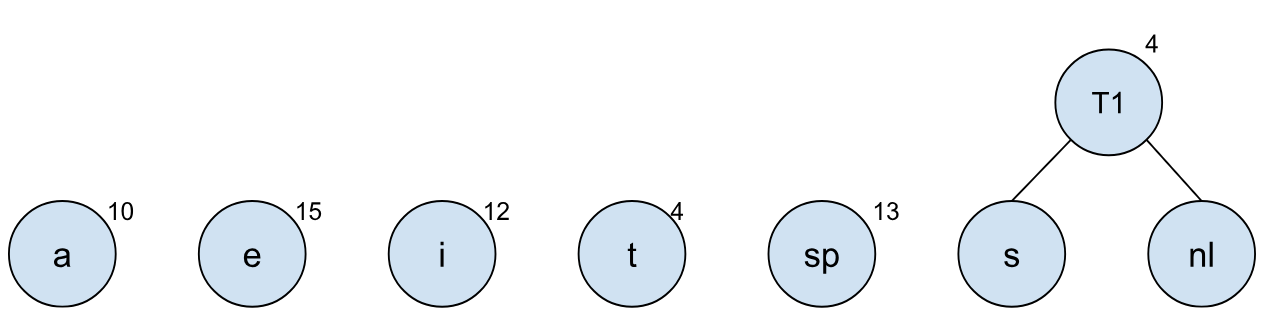
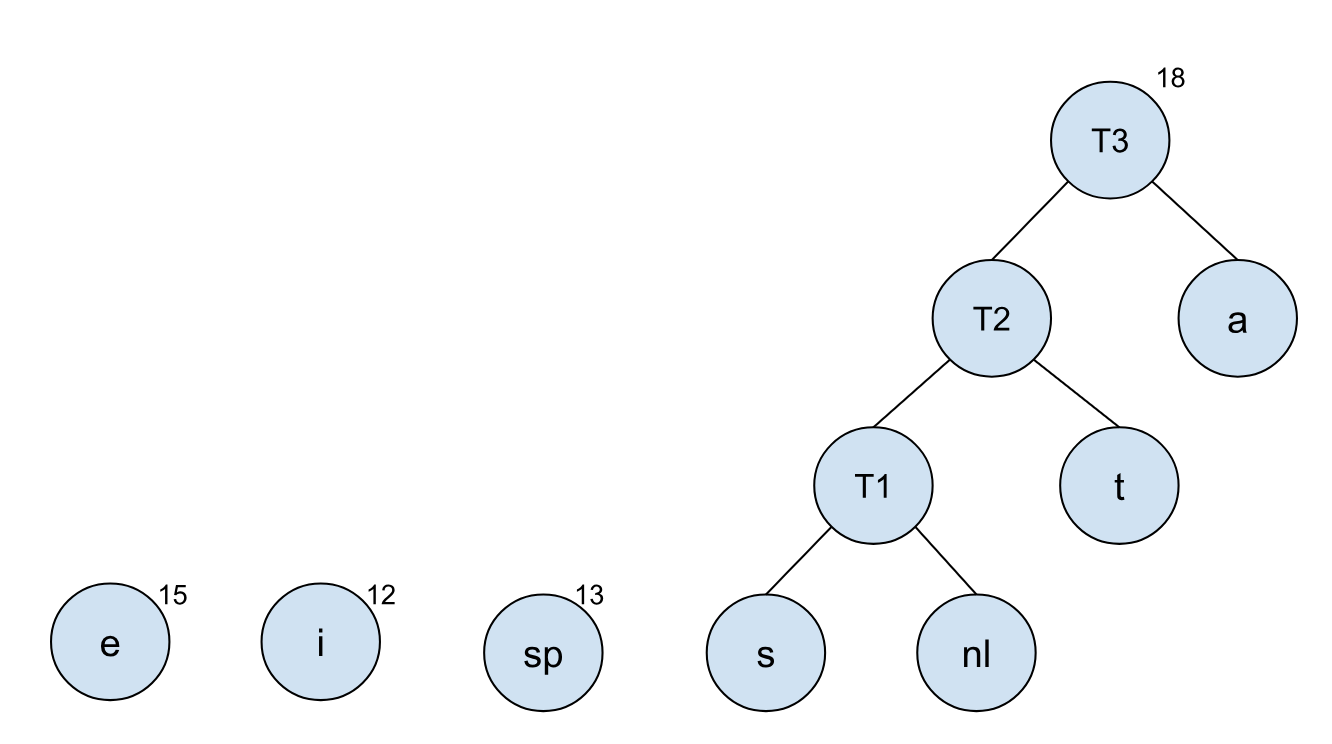
一开始我们把所有的字符都当成是一个个树节点，树节点对应的频率在左上角：

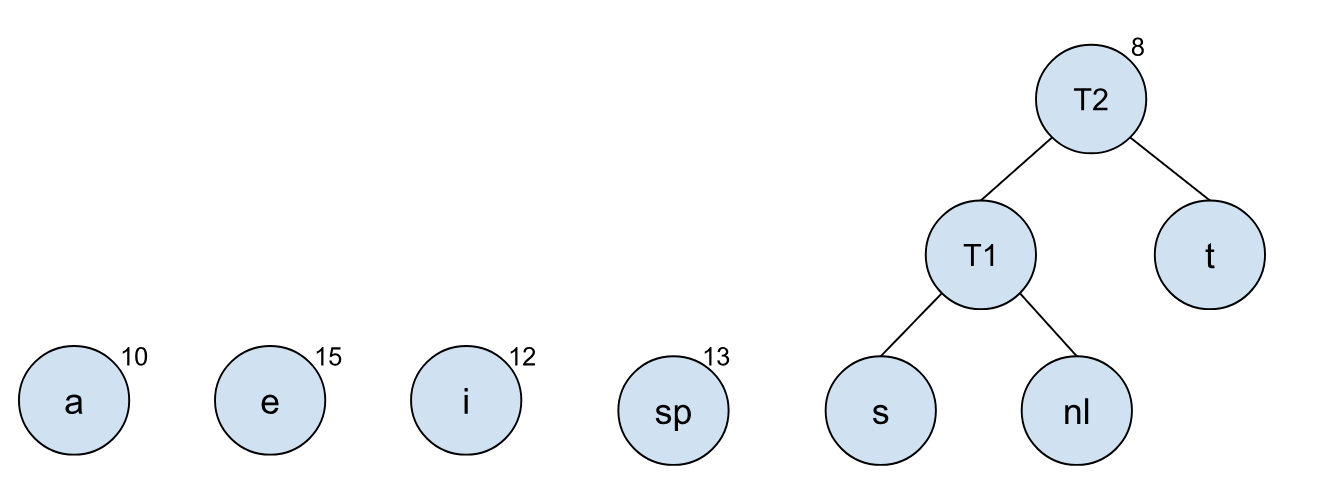
我们首先将字符 s 和 nl 进行合并，并生成一个新的根节点，这样需要合并的树就少了一个：

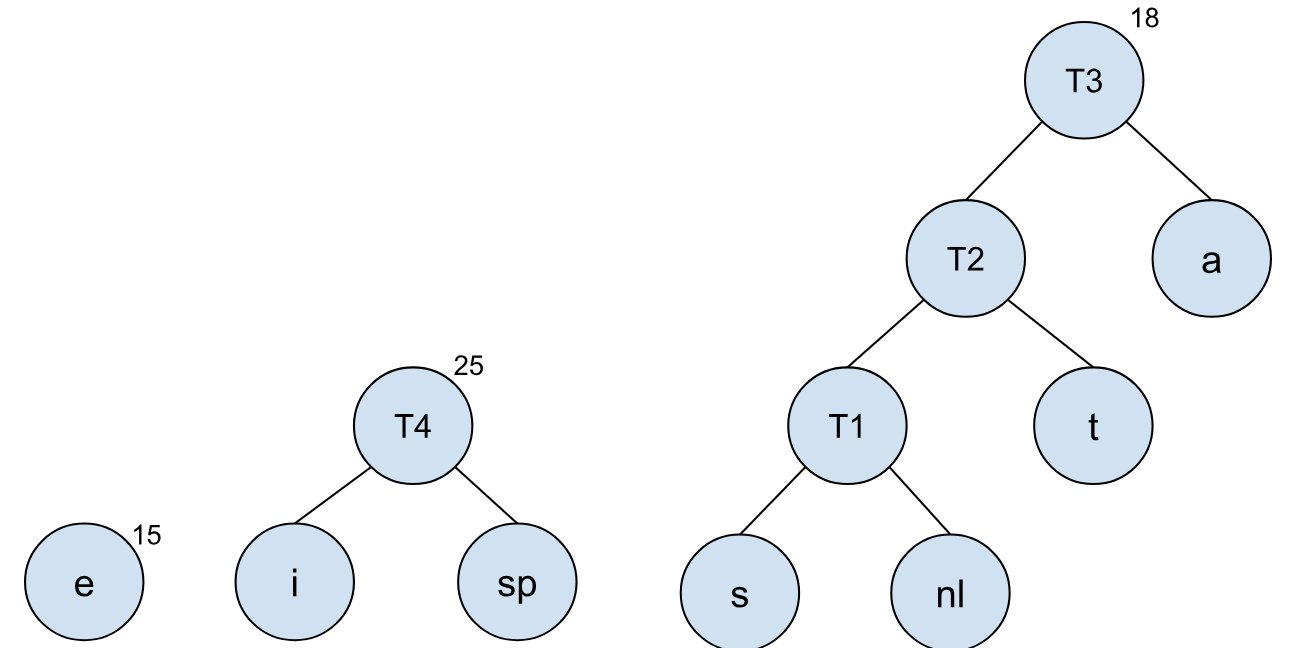
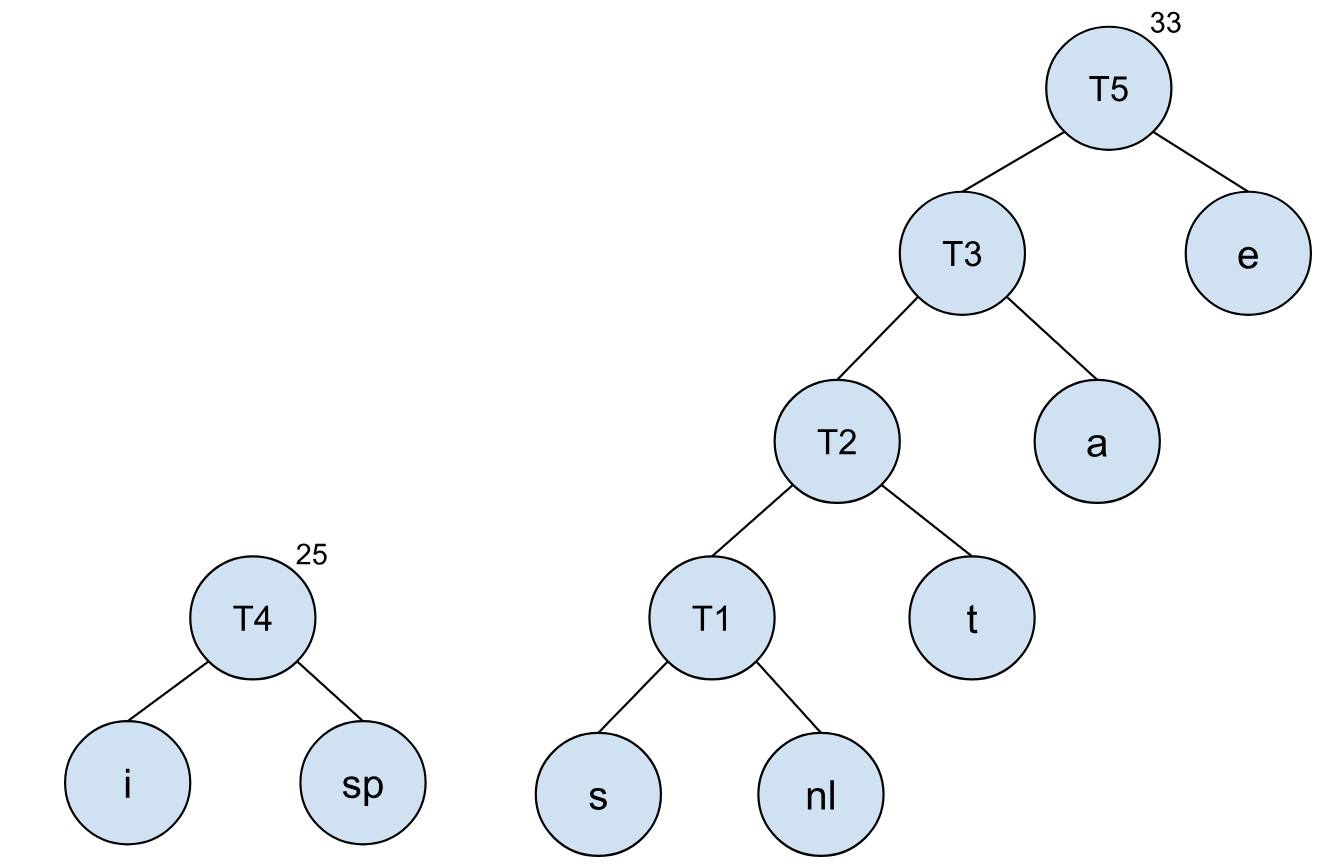
以此类推，我们可以将其他节点依照树的频率，依次合并：

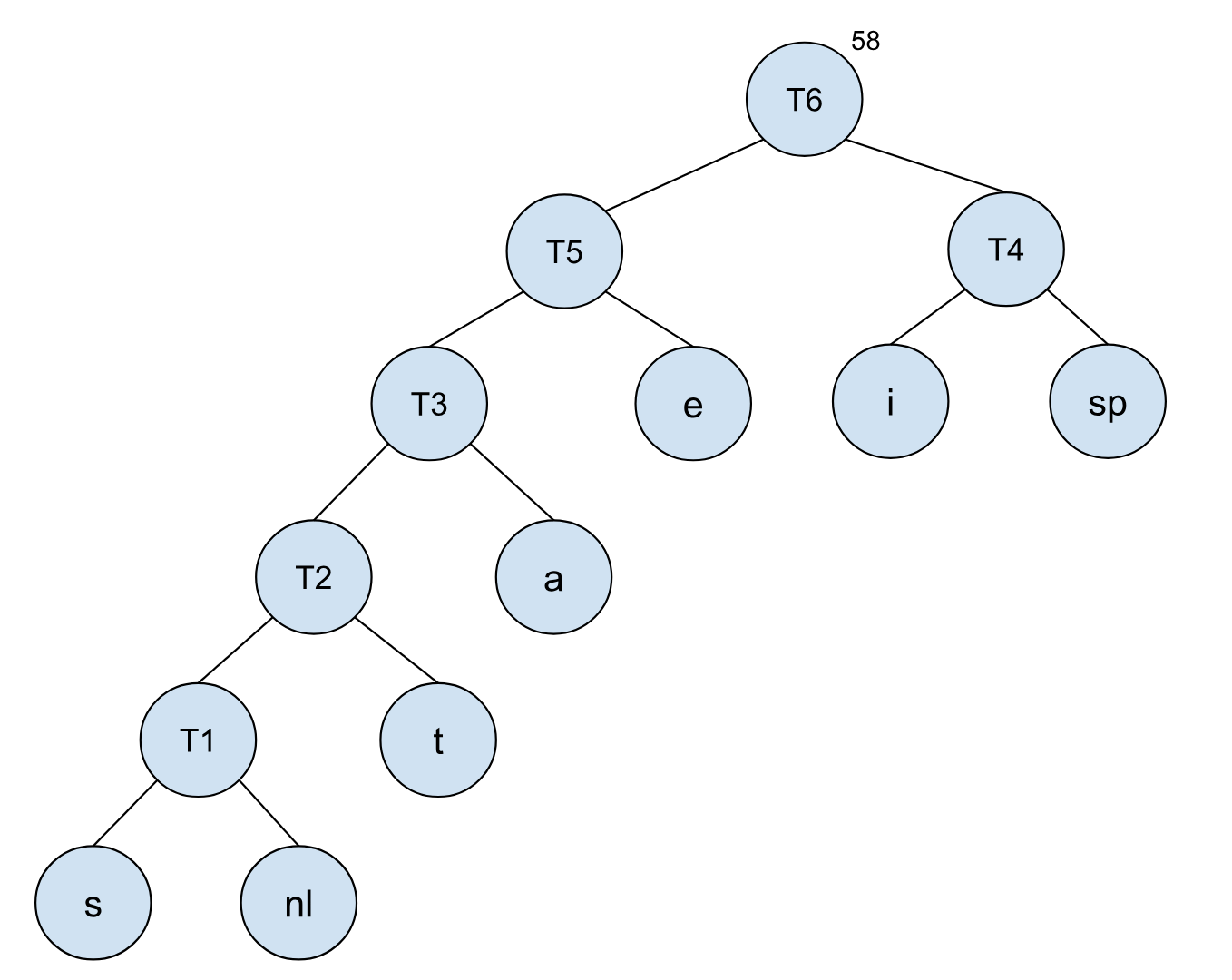
到最后我们就可以得到一个最终的编码树，每个字符所对应的编码也清楚了。

霍夫曼编码的时间复杂度其实是和字符的种类数相关的。如果使用堆的话，操作复杂度就是 O(ClogC)，其中 C 表示的是字符的种类数。但这仅仅是霍夫曼算法的时间复杂度。在实际应用中，我们是需要遍历一边整个文件来获取每个字符出现的频率，还有就是在我们得到具体字符的对应的霍夫曼编码后，我们还需要对整个文件进行重新编码，这个时间复杂度是 O(N) 其中 N 是文件的字符总数。

具体实现

最后，给出霍夫曼算法的具体实现：

class HuffmanNode {
  int freq;
  char c;

  HuffmanNode left;
  HuffmanNode right;
}

class MyComparator implements Comparator<HuffmanNode> {
  public int compare(HuffmanNode x, HuffmanNode y) {
    return x.freq - y.freq;
  }
}

class Huffman {
  public HuffmanNode calculate(HuffmanNode[] chars) {
    if (chars.length < 1) {
      return null;
    }

    PriorityQueue<HuffmanNode> pq = new PriorityQueue<>(
      new MyComparator()
    );

    for (HuffmanNode n : chars) {
      pq.add(n);
    }

    while(pq.size() > 1) {
      HuffmanNode x = pq.poll();
      HuffmanNode y = pq.poll();

      HuffmanNode newTree = new HuffmanNode();
      newTree.freq = x.freq + y.freq;
      newTree.left = x;
      newTree.right = y;
      pq.add(newTree);
    }

    return pq.poll();
  }
}