Post

排序算法之快速排序

Posted
By Yuhang Peng 15 min read

基本思想

前面一篇 文章 我们介绍了归并排序，这篇文章继续介绍另一个比较型排序 - 快速排序。根据算法名称就可以知道，这个排序主打高效，快速排序被包括进 20 世纪最伟大的十大算法，也被改写衍生为其他的算法，比如我们之前提到的 快速选择，这个算法的地位和影响力相信不用我多说了。可有意思的是，从时间复杂度来看，它的最差时间复杂度是 $O(N^2)$，相比于我们前面说的归并排序，以及 堆排序，这让人不太能接受。它究竟快在哪呢？相信通过了解这个算法的实现细节，你就能找到答案。

快速排序和归并排序一样，也是基于分治的思想（如果还不了解什么是分治，可退回去看前一篇文章，这里就不过多赘述）。虽说都是分治，但是在怎么分，怎么合上，这两个算法可谓大相径庭。归并排序的分就是简单地将数组一分为二，重点在合上，合的时候将两个分之后的数组中的元素挨个比较后放到一个新的数组中。而快速排序在分的时候就开始比较了，算法会先从数组中选择一个元素作为基准值，然后每个元素挨个与这个基准值进行比较，由此可按序分成 3 个区间，分别是，小于基准值的，等于基准值的，大于基准值的，然后递归地去排小于基准值和大于基准值的部分。合的话就相对来说简单了，或者说基本上不用合，因为上面这 3 个区间在分的时候就已经确保了顺序。其实大部分时候我们都是分成 2 个区间，这样实现起来会更加方便，我们暂且假设元素是不重复的，我们后面再讨论有重复元素的情况，

所以，总的来说，快速排序的操作就如下面这样

  1. 判断问题中需要排序的元素个数，如果是小于或等于 1 个，不需要排，直接返回
  2. 从要排的数据集中选取一个基准值
  3. 将数据集分成两个部分——小于基准值，以及大于基准值
  4. 递归去继续排小于基准值的部分和大于基准值的部分

按照上面的思路，我们可以很轻松地实现一个快速排序出来，但是你以为这就完了吗？

选择优化

上面的思路仅仅是给一个框架，按这个框架实现出来的快速排序可以正常运行，但绝不能说它高效，这里面还有很多的细节需要考虑。快速排序是否高效完全取决于分的均不均匀，这也就对应着前面提到的操作步骤中的 2，3 项。假如说我们每次都选择待排数组中的第一个元素作为基准值，那么如果输入是排好序的，比如 1,2,3,4,5,6,7,8 这样，那么每次分的时候都会导致小于基准值的部分为空，除了基准值，其余元素全跑到大于基准值那边去了，这样整个算法的时间复杂度就退回到 $O(N^2)$。

虽然这个例子比较极端，但是当数组中元素个数非常多，递归去排的话，这种情况发生在子问题中的概率还是非常大的。因此如何选择这个基准值是非常关键的。

单纯地选择头尾，或者某个位置的元素都不是好的策略，这样没法很好地保证随机性。最理想的情况当然是从数组中随机选择一个位置的元素作为基准值，但是如何做到随机呢？使用程序语言自带的随机函数吗？这显然会增加算法的时间复杂度。这里，我们同时选择头、尾、中三个地方的元素，然后选取他们的中间值作为基准值。事实证明这样做能有效降低极端情况发生的次数，从而提升算法的效率。具体的选择实现如下面的函数所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

private static <AnyType extends Comparable<? super AnyType>> AnyType median3(AnyType[] a, int left, int right) {
	int center = (left + right) / 2;
	if (a[center].compareTo(a[left]) < 0) {
    swap(a, left, center);
  }
  if (a[right].compareTo(a[left]) < 0) {
    swap(a, left, right);
  }
  if (a[right].compareTo(a[center]) < 0) {
    swap(a, right, center);
  }
  swap(a, center, right - 1);
  return a[right-1];
}

这里，我们不但找出了中间值，并且还通过交换位置，将这三个值从小到大摆放。最后有一个细节是我们把中间元素放到了倒数第二位，这样做的好处是，在接下来的遍历比较操作中，这三个元素都不会被考虑进去，提升了效率。

去重优化

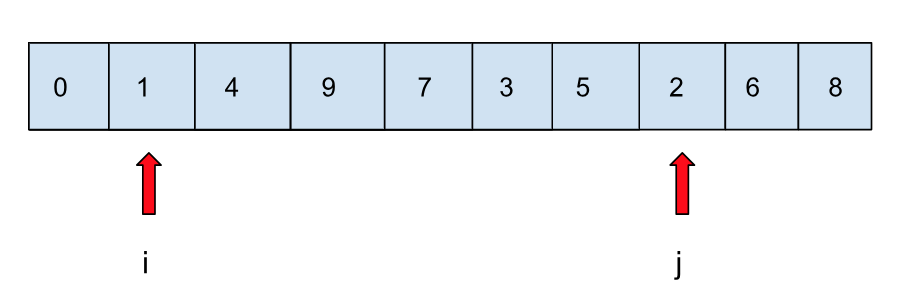
选择好了基准值，剩下的事情就是分了，分的过程我们会通过两个相向的指针来完成，假设我们需要对数组 [8,1,4,9,6,3,5,2,7,0] 进行排序。通过上面的选择基准值，我们可以把数组变成下面这样：

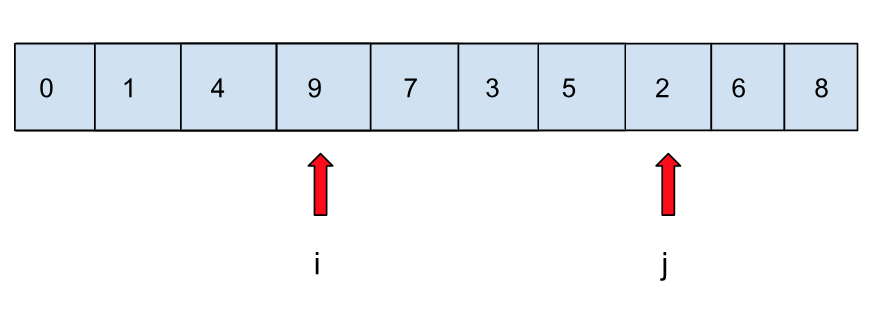
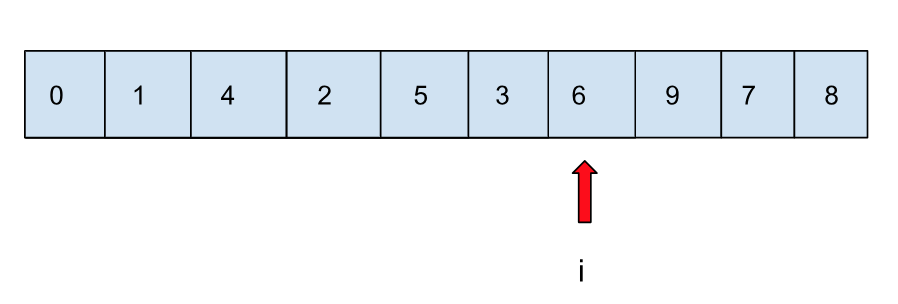
这里有两个指针做相向移动，左边的指针 i 移动到比基准值大的地方停住，右边的指针 j 移动到比基准值小的地方停住，两个指针都停住时进行交换：

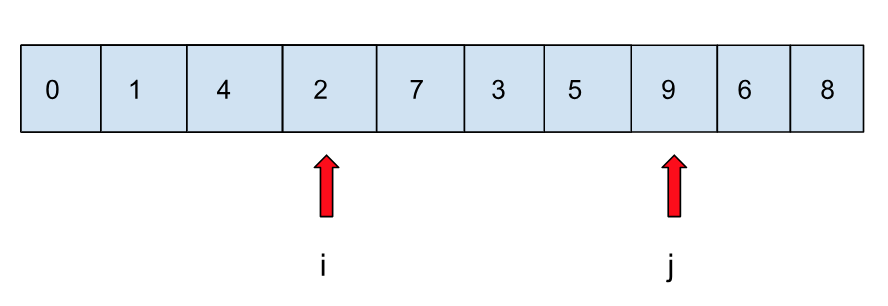
以此类推，直到两个指针相互移动到对方的区域：

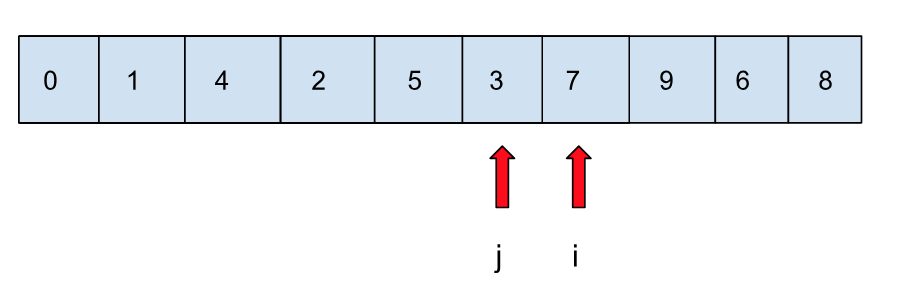
可以看到，结束的时候，i 与 j 都指向对方区域的边界元素，这时还剩最后一步，就是将之前放在倒数第二位的基准值和的 i 指向的元素交换：

这样整个分的过程就算是结束了，剩下的事情就是对 i 左边区域以及 i 右边区域再递归下去。

回到文章前面遗留的问题，如果数组中存在重复的元素，我们该如何分呢？也就是说在双指针遍历的过程中遇到和基准值相同的元素，我们到底把它放到左边还是放到右边呢？很显然，不管是放左边还是放右边，都会造成偏见，考虑一个极端情况，假设整个数组的元素相同，比如 [1,1,1,1,1,1,1]，只放一边的话，最后算法就会因为分的不均匀而退化至 $O(N^2)$，所以我们两遍都得放。

这里还有一个重点是，左右两个指针遇到和基准值相同的元素要停止移动，所以上面的极端情况，i，j 指针每向前移动一步就要做一次交换。可能有人会觉得，这有必要吗？元素都相同了还交换个啥，直接跳过不更好吗？就这个例子来说，如果我们做不交换，就会导致一个指针一直移动到尽头，最后算法还是会退化为 $O(N^2)$，相反地，做了交换，虽然耗费了些常数级复杂度，但是最后整个数组基本上是被等分的，这也是我们希望看到的。

具体实现与分析

由上面的分析，我们可以得到下面的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

public static <AnyType extends Comparable<? super AnyType>> void quicksort( AnyType [ ] a ) {
  quicksort( a, 0, a.length - 1 );
}

private static <AnyType extends Comparable<? super AnyType>> void quicksort(
  AnyType [ ] a, int left, int right
) {
  // 快速排序对小数组（size <= 10）的排序效率没有提升，改为插入排序效果更好
  if(left + CUTOFF <= right ) {
    // 获得基准值，并将左中右三个元素依照大小对号入座
    // 基准值被放在倒数第二的位置
    AnyType pivot = median3(a, left, right);

    // 由于前面的 3 个元素以按序放到指定位置了
    // 这里 i 从 left+1 起始，j 从 right-2 起始
    int i = left, j = right - 1;
    for( ; ; ) {
      while( a[++i].compareTo(pivot) < 0 ) {}
      while( a[--j].compareTo(pivot) > 0 ) {}

      if(i < j) {
        swapReferences(a, i, j);
      } else {
        break;
      }
    }

    // 回复基准值的位置
    swapReferences(a, i, right - 1);

    // 递归对左右区间再进行排序
    quicksort(a, left, i - 1);
    quicksort(a, i + 1, right);
  } else {
    insertionSort(a, left, right);
  }
}

可能很多人会对上面代码中 i，j 的初始值有疑惑，为什么不直接写成下面这样呢？

1
2
3
4
5
6
7
8
9
10
11

int i = left + 1, j = right - 2;
for( ; ; ) {
  while( a[i].compareTo(pivot) < 0 ) { i++; }
  while( a[j].compareTo(pivot) > 0 ) { j--; }

  if(i < j) {
    swapReferences(a, i, j);
  } else {
    break;
  }
}

这其实很细节，上面的代码中，当 a[i] == a[j] == pivot 时就会出问题，因为等于基准值时是需要停止遍历的，这时 i，j 停止遍历的同时，也不再移动，整个 for loop 就陷入了死循环。

到此，整个快速排序的思路和实现都讲了，回到一开始的问题，快速排序究竟为什么快速？如果你把上面的代码与之前的归并排序做一个对比就清楚了，归并排序需要将整个数组中的元素都复制到另一个数组中，而快速排序除了指针的加减，基本上所有的操作都是 in-place 的，虽然说也有元素的交换，但是这些交换都发生在一个连续的地址空间内，这种情况下编译器可以对其优化，让其机器级指令更加地精简，从而获得效率的提升。这部分性能的提升完全弥补了不能等分的劣势，实际运行来看，上面的代码很少出现极端情况，并且由于常数级的消耗更少，相比于其他排序算法，快速排序会更加高效。

快速排序有一个问题是它的不稳定性，对于两个值相等的元素，快速排序没法保证它们在排序后的相对位置不变，当然，很多情况并不需要稳定的排序，如果需要稳定的排序，我们可以使用归并排序。毕竟算法再好，也不是任何情况下都适用，软件世界里，没有银弹，这句话从来都没有例外。

日志, 算法
算法 排序
This post is licensed under CC BY 4.0 by the author.