排序算法之堆排序

堆排序算法介绍

在之前的 文章 中，我们介绍了堆这个数据结构，并且给出了它的各项操作的实现。

堆最主要的特性是可以在 O(1) 的时间里获取一个数据集中的最值。在之前的 文章 中，我们也详细推导了构建一个含有 N 个元素的堆只需要 O(N) 的时间。并且我们其实都知道，从堆中删除一个元素（一般是删除最值）只需要 O(logN)。

知道了这些，我们能否基于堆的这些特性来对一组数据进行排序呢？答案是肯定的，直观来看，只需要 2 步：

• 基于输入的数据集构建堆（花费 O(N) 时间）
• 重新创建一个数组，从堆中移除最值放到这个数组中，重复 N 次（花费 O(NlogN) 时间）

上面两步的时间加起来最终的时间复杂度是 O(NlogN)。

光从时间复杂度来看，这个算法挺优秀的。美中不足的是，第 2 步的时候，我们用了额外的空间，那我们这里能不能优化呢？

堆排序的优化与实现

初看堆排序还是挺直观的，无非是借助堆的特性来对元素进行重新组合。但是这里我们是否真的需要重新创建一个数组？其实我们依然可以在原数组内进行排序，那具体该如何做呢？

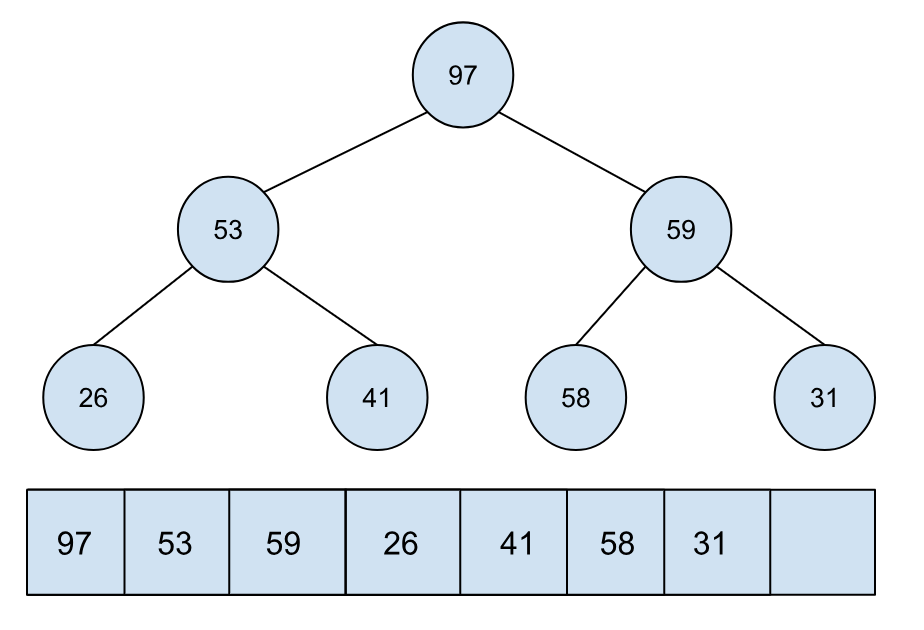
我们知道堆其实可以用数组来表示，比如下面这个例子中的最大堆有 7 个元素：

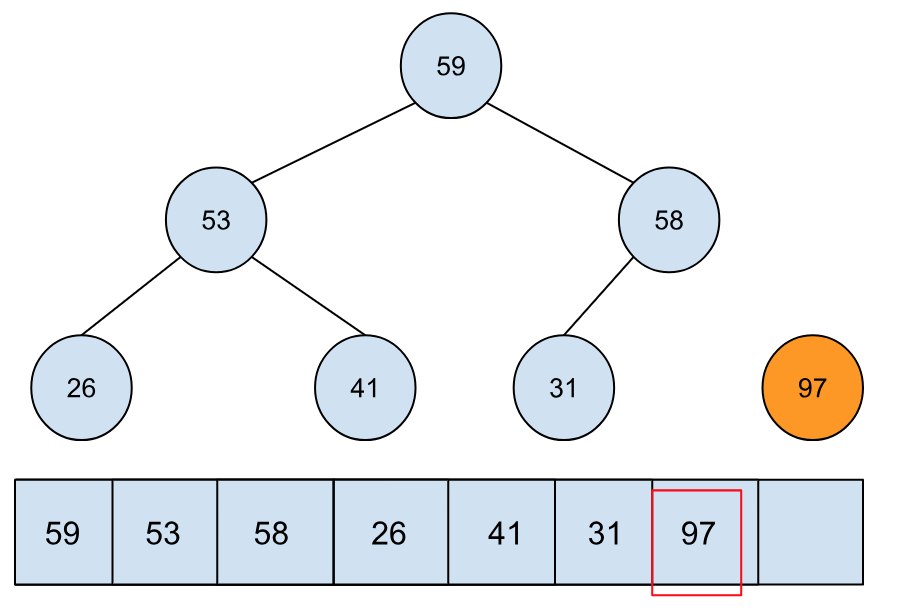
当我们将最值从堆中移除，也就是这里的 97。移除后的堆的大小就变成了 6，这时我们可以将移除后的元素放到堆的最末尾：

这个操作并不会影响堆的运作，当你采用这个方式将堆中的元素全部移除后（其实最后一个元素不需要移除），最后的数组就是排好序的。

这个操作可以避免创建新的数组，节省了空间。

最后，给出堆排序的具体实现：

private static int leftChild(int i) {
  return 2 * i + 1;
}

private static <AnyType extends Comparable<? super AnyType>> void swapReference(AnyType[] a, int i, int j) {
  AnyType tmp = a[i];
  a[i] = a[j];
  a[j] = tmp;
}

private static <AnyType extends Comparable<? super AnyType>> void percDown(AnyType[] a, int i, int n) {
  int child;
  AnyType tmp;

  for (tmp = a[i]; leftChild(i) < n; i = child) {
    child = leftChild(i);
    if (child != n - 1 && a[child].compareTo(a[child+1]) < 0) {
      child++;
    }

    if (tmp.compareTo(a[child]) < 0) {
      a[i] = a[child];
    } else {
      break;
    }
  }
  a[i] = tmp;
}

public static <AnyType extends Comparable<? super AnyType>> void heapsort(AnyType[] a) {
  // 构建堆
  for (int i = a.length / 2 - 1; i >= 0; i--) {
    percDown(a, i, a.length);
  }

  // 通过删除最值来排序
  for (int i = a.length - 1; i > 0; i--) {
    swapReferences(a, 0, i);
    percDown(a, 0, i);
  } 
}

如果你清楚堆的具体实现，那么堆排序对于你来说还是非常直观的。虽然说堆排序的时间复杂度可以达到 O(NlogN)，但是它在实际场景中的使用还是不是很普遍。

虽然整体的时间是 O(NlogN)，但是实际的运行效率并不是特别高效。主要原因在于，堆排序除了元素之间的比较，还依赖于很多辅助操作，比如构建堆，通过下标定位元素的位置，以及通过多次交换以维持堆的结构等等，这些操作都会增加元素交换的数量。

此外，相比于其他的基于分治算法的排序，比如归并排序，以及快速排序，堆排序元素的比较从头到尾都是全局的，这对缓存很不友好。