堆的基本概念和操作

Posted Sep 29, 2023

By Yuhang Peng 16 min read

堆（在 Java 中被称为优先队列）能够在常数时间内获取一个数据集合中的最值，更重要的是，这个数据结构在排序、文件合并、以及一些筛选算法中都有广泛的应用。

基本概念与结构

这篇文章我们介绍的堆是 二叉堆（Binary Heap），这是最简单也是最基础的堆结构。一般来说，没有特指，堆指的就是二叉堆。在此结构基础上进行调整，我们可以得到其他更为复杂的堆结构，比如二项堆（Binomial Heap）、左倾堆（Leftist Heap）、斜堆（Skew Heap）、d叉堆（d-Heap）。斐波拉契堆（Fibonacci Heap）等等。这些堆都是由二叉堆衍生出来，用于解决特定问题的数据结构。相信在理解了二叉堆后，我们有能力去学习这些堆的原理与实现。

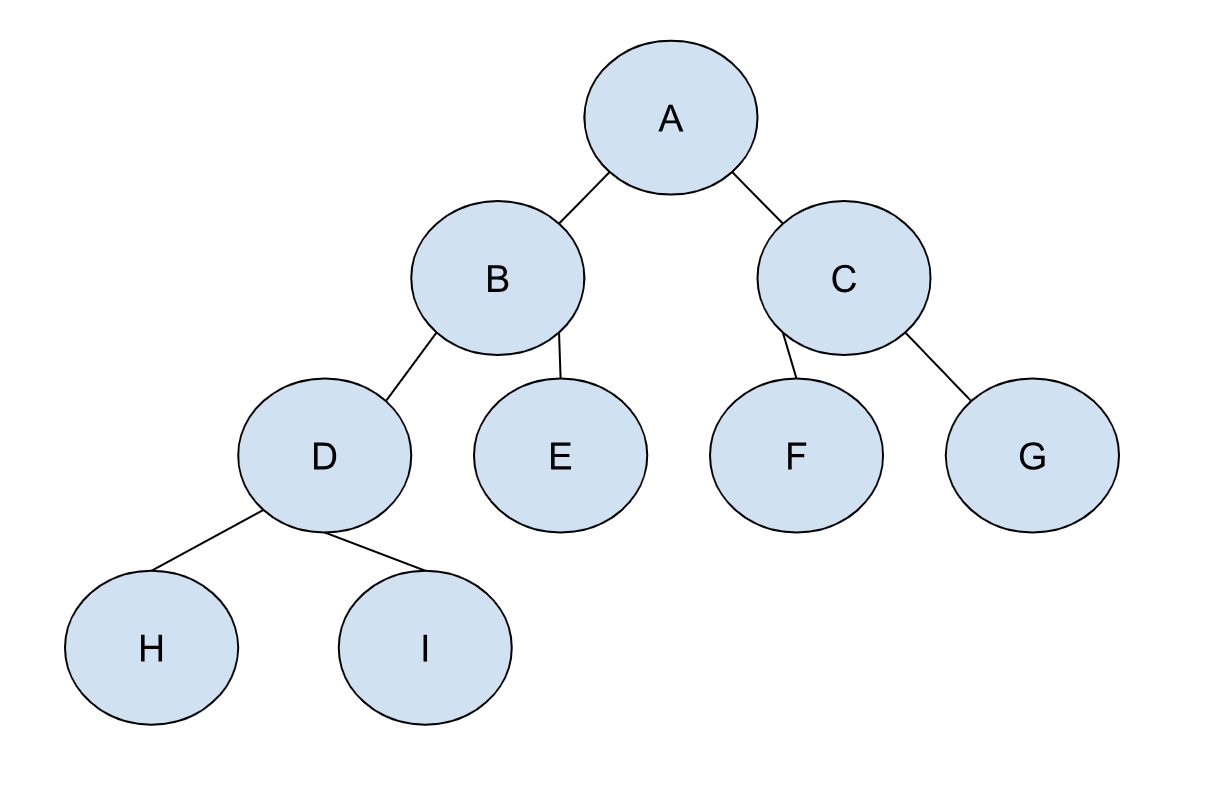
二叉堆的其实就是二叉树，说的更准确些，是一个完全二叉树，如下图显示的：

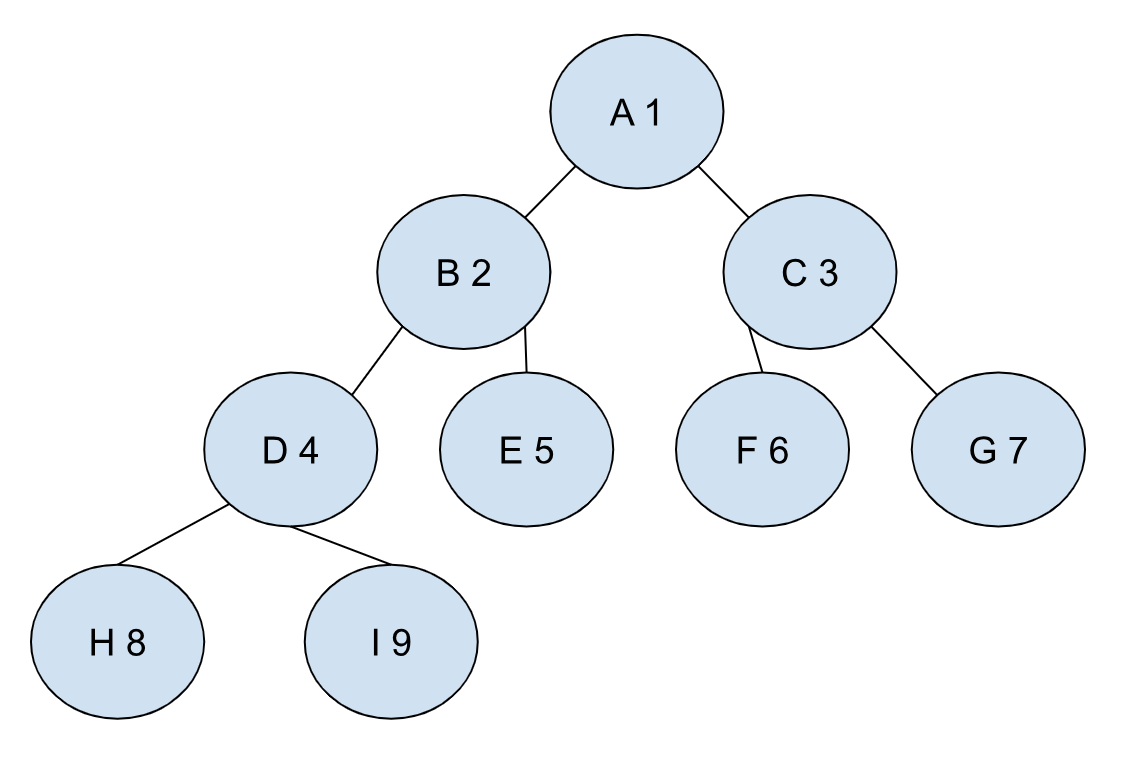
那这么说，是不是我们可以用操作二叉树的方法来操作堆？比如用树节点来表示堆节点，用树的各种遍历来遍历堆？这么做当然没错，但这里我们显然没有用到堆的特性————一个完全二叉树。完全二叉树意味着树是被逐层填满的，我们可以利用这个性质来寻找更为高效的表示方式。当我们把二叉树的每个节点从上到下，从左到右依次表上序号，上图就会显示成下图这样：

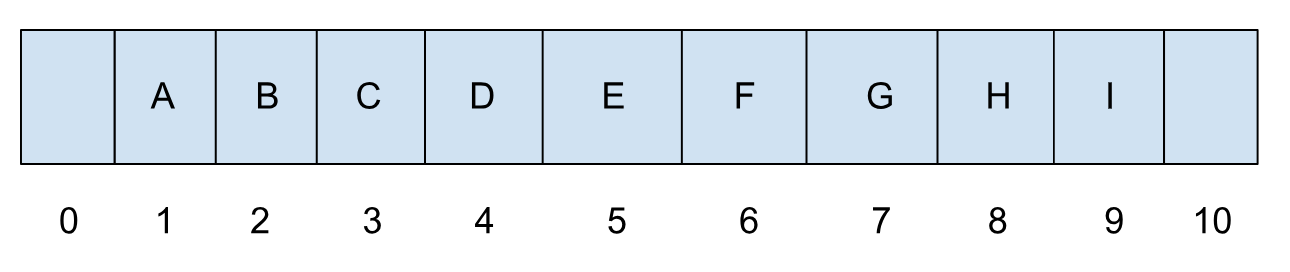
很容易发现，如果某个节点的标号是 i，那么它的左子节点的标号就是 2 * i，右子节点的标号就是 2 * i + 1，父节点的标号是 i / 2。知道了这些有什么用呢？想想看，既然通过下标运算就可以准确无误地确定左右节点，还有父节点，那我们还有必要单独创建树节点来存放这些信息吗？显然没有必要，一个简单的数组就足够了：

数组带来的好处是空间的节省以及访问速度的提升，但是用数组来表示堆并没改变它原本的结构，那它又是如何做到在 O(1) 的时间获得极值的呢？

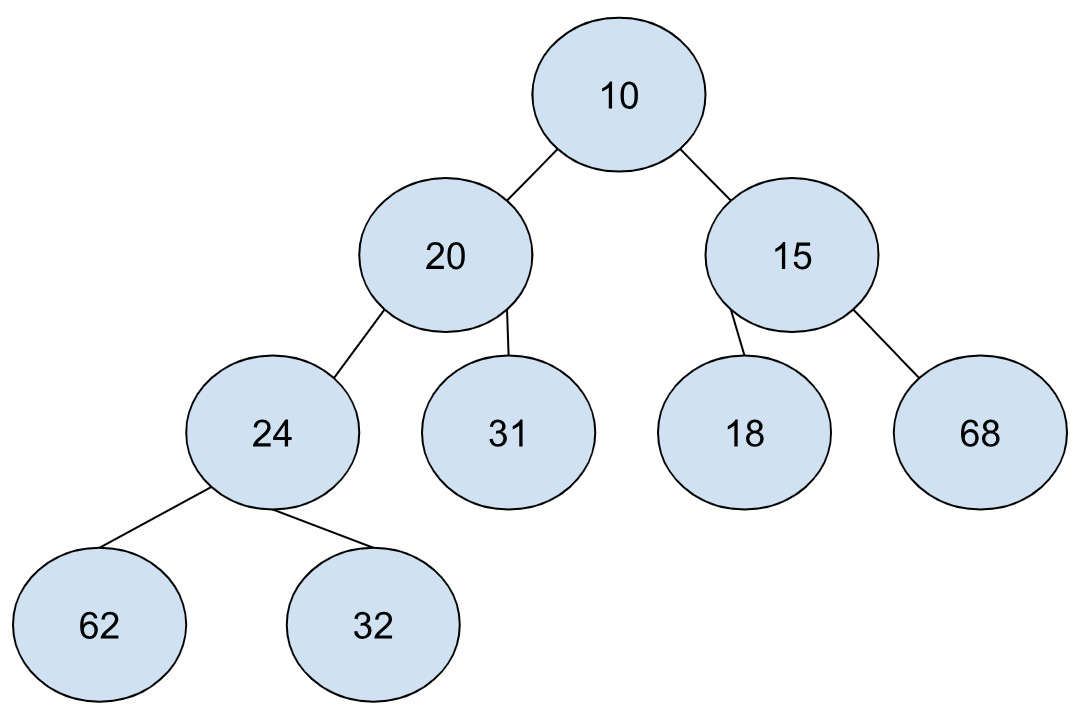
这里就不得不说堆中的元素的排列顺序了，把之前的图例用整形来表示，可以得到下面这个例子：

上面这个例子就是一个最小堆，我们可以看到，每个节点都比它的子节点小，因而根节点存放的就是最小值，这样，我们无需任何遍历就可以直接获得最小值。

当然，除了最小堆，还有最大堆，堆的结构限定我们没法同时获得最大值和最小值，除非维护两个堆。

基本操作

获取极值仅仅是堆的特殊查找操作。一个数据结构还必须要有一些基本操作来保证该数据结构的可用性，堆也不例外。

插入

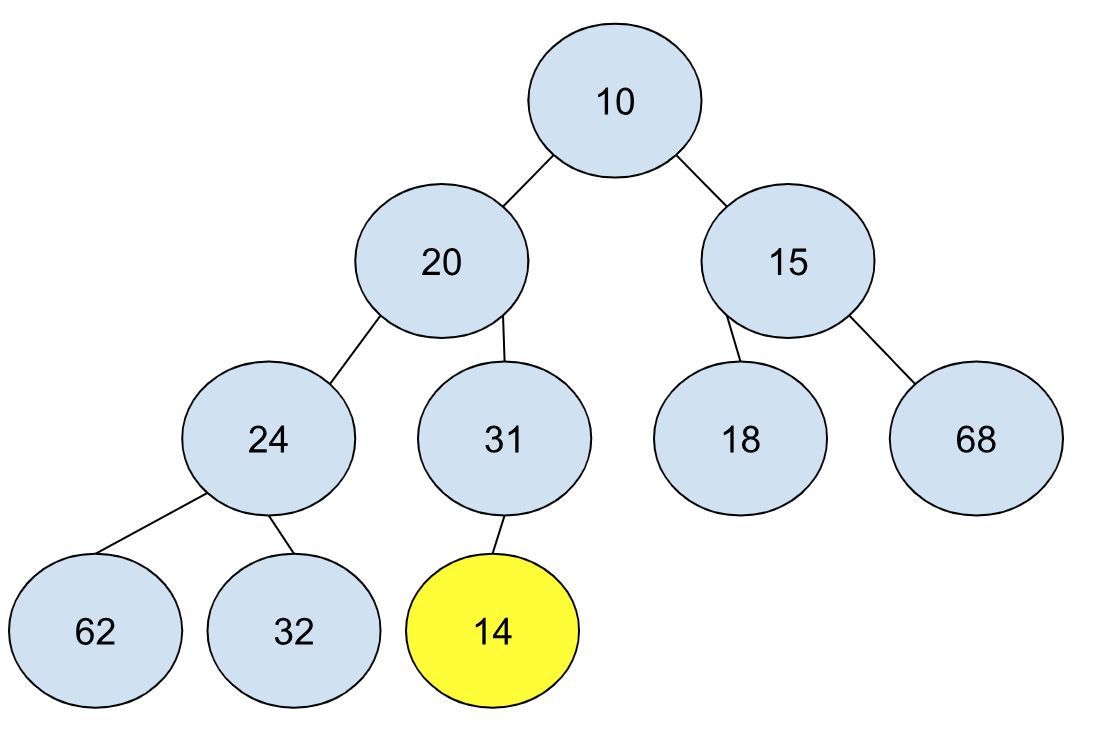
上面提到，堆其实是一个完全二叉树，它的节点是从上到下、从左到右逐层填充的，当有新元素进来，就很自然地被放在指定的位置。比如还是之前的例子，当有一个新的元素（14）进来，最开始我们可以得到如下的结构：

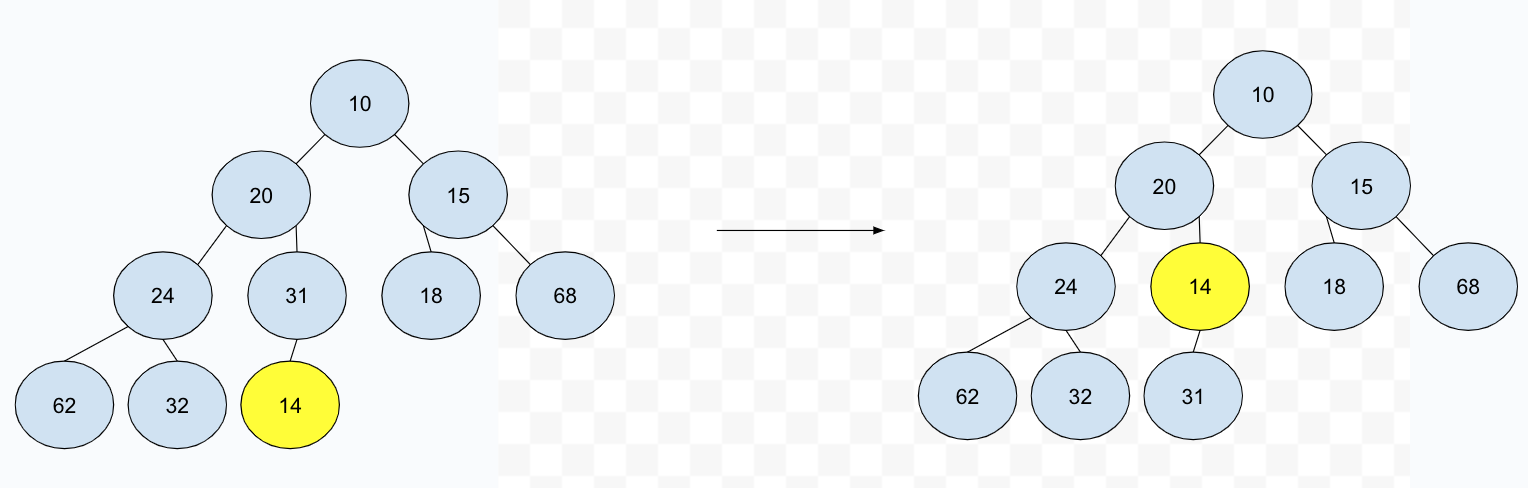
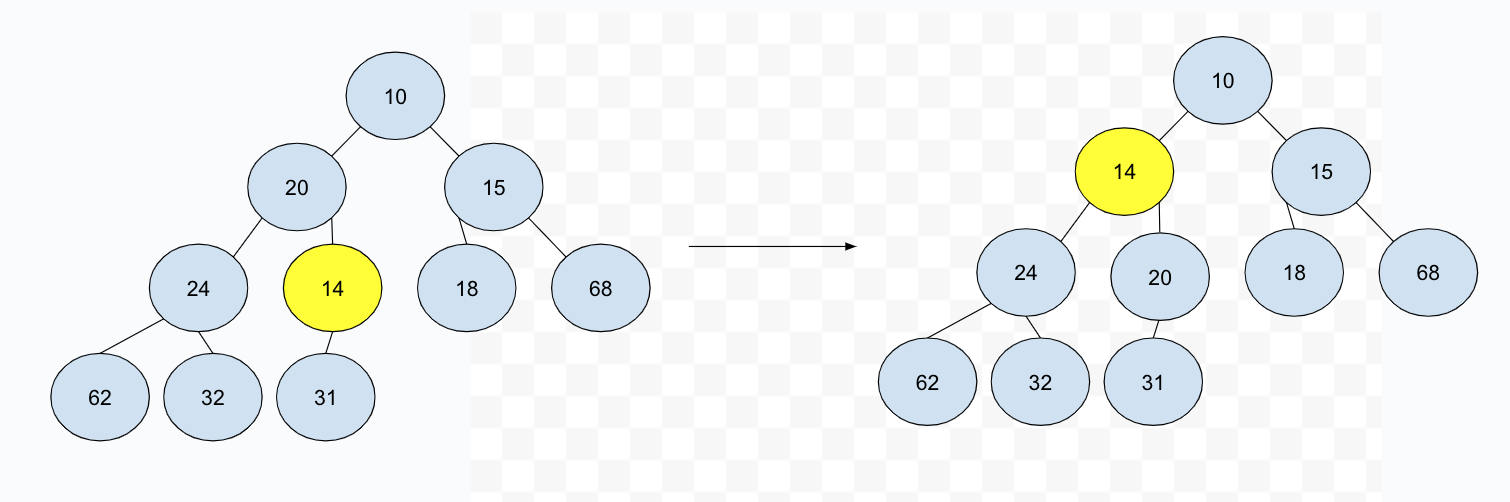
你可能会说，这不对啊，前面我们提到堆的特性————每个节点都比它的子节点小/大————不就被破坏了吗？先不急，很多事情没办法一步到位。因为新插入的节点比它的父节点小，那么我们将其向上与父节点交换不就可以解决问题吗？只要是发现子节点比父节点小，我们就向上交换。上面这个例子，我们只需交换两次就可以维护堆的结构：

这个操作被称作 percolate up，可以理解是上提的意思。当然了，这个操作需要的时间复杂度显然就不是常数级别的了。这个时间复杂度和深度有关，因为是完全二叉树，最差就是 O(logN)，其中 N 是堆中总共的元素个数。

相对应的代码实现：

  
public void insert(AnyType x) {
  if (currentSize == array.length - 1) {
    enlargeArray(array.length * 2 + 1);
  }

  int hole = ++currentSize;
  // percolate up
  for (array[0] = x; x.compareTo(array[hole/2]) < 0; hole /= 2) {
    array[hole] = array[hole / 2];
  }
  array[hole] = x;
}

删除最小值

有插入就有删除，但是在堆中，除了最值，我们很难根据元素的值对应到堆中的节点（除非完整遍历或借助其他数据结构）。因此，删除操作最直接的就是针对最值，也就是根节点。

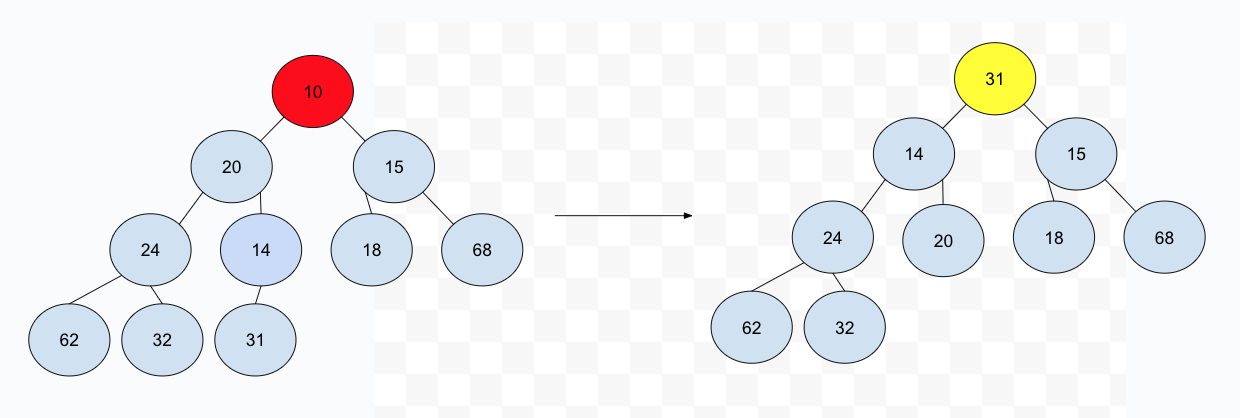
删除意味着某个位置的元素被移除，但是在堆中，我们需要保证完全二叉树的结构，势必有其他的元素填补进来。那具体用哪个元素来填入？当然是最末尾的元素————这不会影响到其他的节点，也不会破坏完全二叉树的结构，我们还是拿之前的例子来说明，当根节点被删除后，我们用最末尾的元素进行填补：

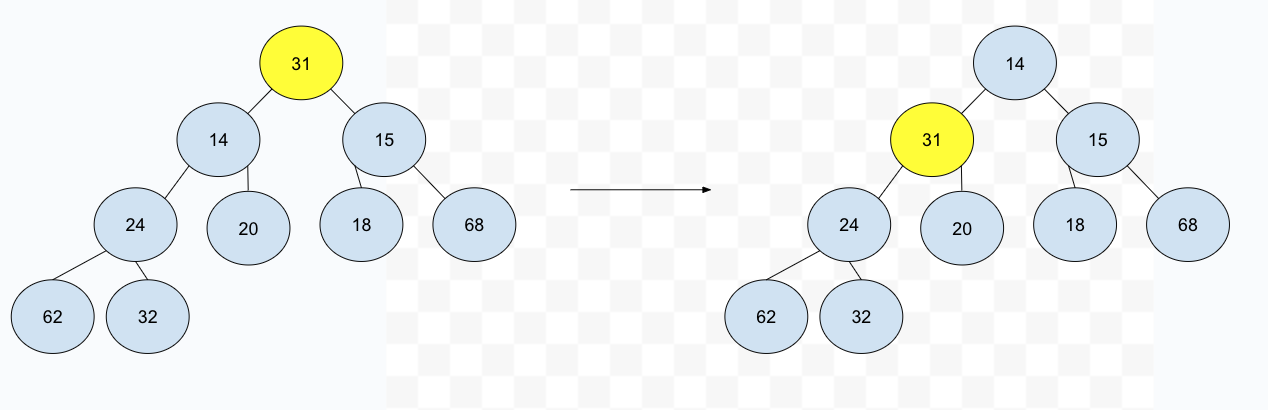
这么做的问题也是明显的，堆的特性————每个节点都比它的子节点小————被再次破坏，我们对其调整就是了。

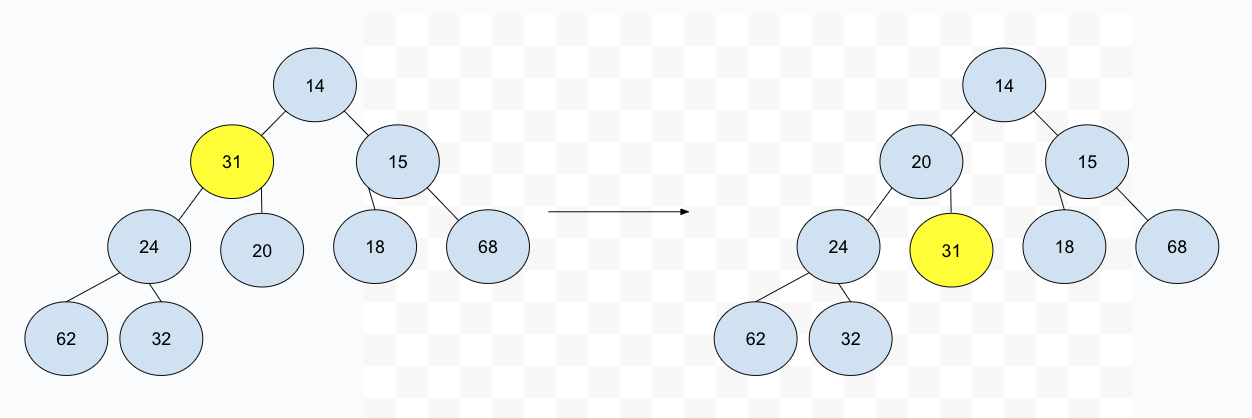
在插入操作中，我们提到了 perlocate up 这个操作，类似地，我们也可将相对应的子节点下移，比如这个例子中，我们就可以将 31 这个节点和其最小的子节点交换，依次进行下去，直到叶子节点：

这个操作被称作 percolate down，和之前的 perlocate up 相对应，相信不难理解。操作的时间复杂度也是和之前一样————O(logN)。

相对应的代码实现如下：

  
public AnyType deleteMin() {
  if (isEmpty()) {
    throw new UnderflowException();
  }

  AnyType minItem = findMin();
  array[1] = array[currentSize--];
  percolateDown(1);

  return minItem;
}

private percolateDown(int hole) {
  int child;
  AnyType tmp = array[hole];

  for (; hole * 2 <= currentSize; hole = child) {
    child = hole * 2;
    if (child != currentSize && array[child + 1].compareTo(array[child]) < 0) {
      child++;
    }

    if (array[child].compareTo(tmp) < 0) {
      array[hole] = array[child];
    } else {
      break;
    }
  }
  array[hole] = tmp;
}

构建堆

按理说，有了找最值操作以及上面两个操作，堆的基本操作就有了，应对常规的场景是没有问题的。但是很多时候我们需要基于一些现存的元素来构建一个堆。你可能会说，批量的插入不就可以解决问题吗？的确，如果假定元素的个数是 N，每次插入的时间是 O(logN)，批量插入到最后的时间复杂度貌似是 O(NlogN)。那有没有更加高效的方法呢？

假设我们先不管堆的特性，直接构建完全二叉树，也就是直接填充数组，这个时间复杂度是 O(N)。在此基础之上，我们只需要对非叶子节点的元素进行 perlocate down 操作即可，代码实现如下：

  
public BinaryHeap(AnyType[] items) {
  currentSize = items.length;
  array = (AnyType[]) new Comparable[(currentSize + 2) * 11 / 10];

  int i = 1;
  for (AnyType item : items) {
    array[i++] = item;
  }
  buildHeap();
}

private void buildHeap() {
  for (int i = currentSize / 2; i > 0; i--) {
    percolateDown(i);
  }
}

那么这样做时间复杂度不还是 O(NlogN)？

对于单一的 percolate down 操作的时间复杂度的确是 O(logN)，但请注意这个是最差的时间复杂度，换句话说如果我们对根节点进行 percolate down，并且交换一直进行到最后的叶子节点，那确实需要 logN 次比较和交换。但是问题是一颗树上不是所有的节点都是根节点，也不是所有的节点的 percolate down 操作都需要 logN 次比较和交换，比如对某个叶子节点的父节点进行 percolate down，可能就只需要 1 次比较和交换。可见 O(NlogN) 的结论并不准确，我们需要通过其他方式来分析其时间复杂度。

通过观察，我们可以发现通过 percolate down 构建堆的所需要的操作次数是和树的高（height）相关的，准确地说，树上所有节点的高相加就是操作的次数。

我们假设树的高是 h，也就是根节点的高是 h，每往下一层，高度减一，到叶子节点，高度就是 0。因为是完全二叉树，节点个数 N 其实就满足

\[2^h <= N <= 2^{h+1} - 1\]

所有节点的高度和是

\[S = h + 2(h-1) + 4(h-2) + 8(h-3) + ... + 2^{h-1}(1)\]

我们将上面式子两边同时乘上 2 可以得到

\[2S = 2h + 4(h-1) + 8(h-2) + 16(h-3) + ... + 2^{h}(1)\]

将上述两个式子错位相减，比如 2h - 2(h-1)，4(h-1) - 4(h-2)，我们可以得到带常数项的式子

\[S = -h + 2 + 4 + 8 + ... + 2^{h-1} + 2^{h}\]

应用等比数列公式，可以得到

\[S = (2^{h+1} - 1) - (h + 1)\]

所以，节点的高度之和 S 与节点个数 N 的关系是

\[S = aN\]

其中 a 是小于 2 的常数，这就说明这个算法的时间复杂度是 O(N)，而不是 O(NlogN)。

总结

除了上述基本操作外，还有一些特殊的操作，比如根据元素的位置来更改或者删除元素，这些操作也是通过 percolate up 或者是 percolate down 来维护堆的特性，并且，这些操作在实际场景中的应用需结合其他的数据结构，比如散列表，这里就不过多赘述。

将上述的代码整个成类，完整的实现代码如下：

  
public class BinaryHeap<AnyType extends Comparable<? super AnyType>> {
  private static final int DEFAULT_CAPACITY = 10;
  private int currentSize;     // Number of elements in heap
  private AnyType[] array;     // The heap array

  public BinaryHeap() { /* 略 */ }
  public BinaryHeap(int capacity) { /* 略 */ }
  public BinaryHeap(AnyType[] items) {
    currentSize = items.length;
    array = (AnyType[]) new Comparable[(currentSize + 2) * 11 / 10];

    int i = 1;
    for (AnyType item : items) {
      array[i++] = item;
    }
    buildHeap();
  }

  public void insert(AnyType x) {
    if (currentSize == array.length - 1) {
      enlargeArray(array.length * 2 + 1);
    }

    int hole = ++currentSize;
    // percolate up
    for (array[0] = x; x.compareTo(array[hole/2]) < 0; hole /= 2) {
      array[hole] = array[hole / 2];
    }
    array[hole] = x;
  }

  public AnyType findMin() {
    return array[1];
  }

  public AnyType deleteMin() {
    if (isEmpty()) {
      throw new UnderflowException();
    }

    AnyType minItem = findMin();
    array[1] = array[currentSize--];
    percolateDown(1);

    return minItem;
  }

  public boolean isEmpty() {
    return currentSize == 0;
  }

  public void makeEmpty() {
    currentSize = 0;
  }

  private percolateDown(int hole) {
    int child;
    AnyType tmp = array[hole];

    for (; hole * 2 <= currentSize; hole = child) {
      child = hole * 2;
      if (child != currentSize && array[child + 1].compareTo(array[child]) < 0) {
        child++;
      }

      if (array[child].compareTo(tmp) < 0) {
        array[hole] = array[child];
      } else {
        break;
      }
    }
    array[hole] = tmp;
  }

  private void buildHeap() {
    for (int i = currentSize / 2; i > 0; i--) {
      percolateDown(i);
    }
  }

  private void enlargeArray(int newSize) { /* 略 */ }
}

日志, 算法, 堆

算法堆

This post is licensed under CC BY 4.0 by the author.

基本概念与结构

基本操作

插入

删除最小值

构建堆

总结

Trending Tags