堆的优化：左倾堆

左倾堆的特性

之前在二项堆的 文章 中提到了普通二叉堆存在的问题，主要就是没法对两个堆进行高效的合并。二项堆可以解决这个问题，除了二项堆以外，今天我们要讲的左倾堆也可以解决这个问题。

在介绍左倾堆之前，有一个概念叫做 零距离（Null Path Length）。对任意一个节点 x，零距离 npl(x) 等于其到最近一个没有两个子节点的节点（不满节点）的长度。

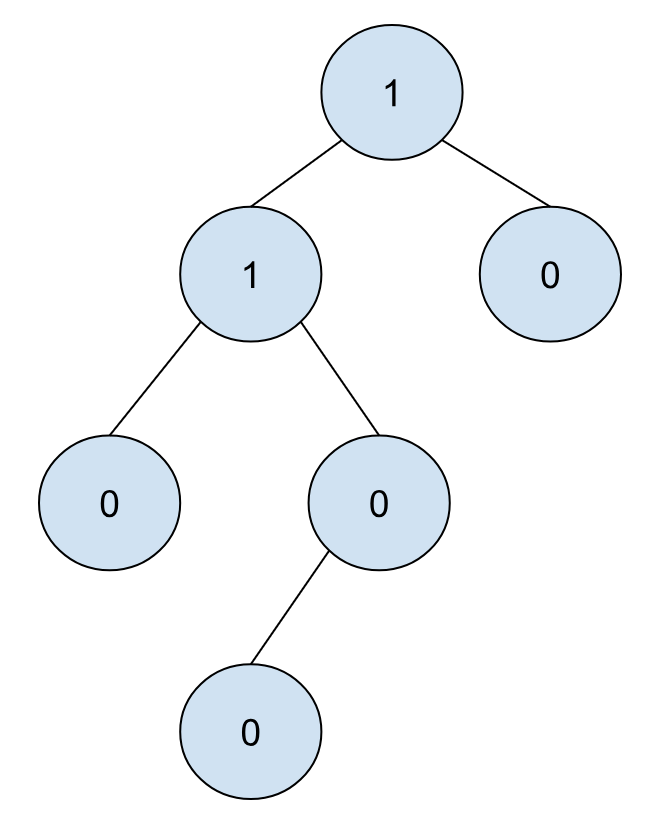
左倾堆是一个特殊的二叉树，特殊之处在于，左倾堆要求任意一个节点 x，它的左子节点的零距离必须大于或者等于右子节点的零距离。比如下面这个图所展示的就是一个左倾堆：

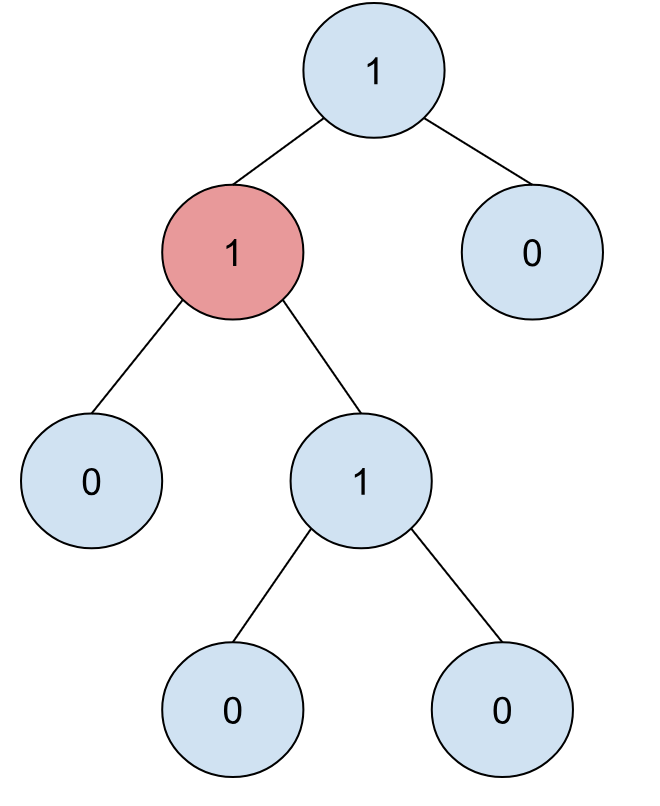
而在上面这颗树上稍作修改，改成下面这颗树，它就不再是左倾堆：

原因也很明显，上图中标红的节点的左右子节点不再满足左倾堆的特性。

从上面的两张图，也可以得到下面的结论：

• 叶子节点和只有一颗子树的节点的零距离为 0
• 空节点（NULL）的零距离为 -1

也正因为左倾堆的这个特性，导致大部分的节点都在左边，右边的路径会相对较短，所以左倾堆的大部分操作都在右边进行，这样可以保证操作的高效，至于说具体的时间复杂度我们后面再进行讨论。

左倾堆的操作

在讲具体操作之前，我们还是来定义一下树的节点，这里因为引入了零距离这个变量，相对于普通的二叉树节点，我们只需要增加一个变量即可：

private static class Node<AnyType> {
  AnyType element;
  Node<AnyType> left;
  Node<AnyType> right;
  int npl;

  // Constructors
  Node(AnyType theElement) {
    this(theElement, null, null);
  }

  Node(AnyType theElement, Node<AnyType> lt, Node<AnyType> rt) {
    element = theElement;
    left = lt;
    right = rt;
    npl = 0;
  }
}

对新构建的节点，零距离都是零，我们会基于具体的操作以及操作之中堆的变化来对其进行更改。

合并

在之前的堆的特性中我们也提到，左倾堆大部分的节点都会在左边，而大部分的操作都在右边，这样操作会更高效。以最小堆为例，合并的逻辑大致如下：

1. 先对比两个堆的根节点的大小，将根节点大的堆合并到根节点小的堆内，这样根节点还是最小
2. 看根节点小的堆左子树是否为空，为空的话直接插入即可，这样不会违背左倾堆的特性
3. 如果左节点不为空，那么就去到右节点，继续重复 1，2

可以看到，左倾堆依旧维持普通堆的元素大小的特性 ———— 子节点均比父节点要大，根节点全局最小。

另外，整个合并过程就是一个递归沿着右路径向下的过程，右路径的长度直接决定了整个操作的时间复杂度。关于具体的时间复杂度分析，我们放在最后，这里只说实现。

可以将上面的思路转换成代码：

public void merge(LeftistHeap<AnyType> rhs) {
  if (this == rhs) {
    return;
  }

  root = merge(root, rhs.root);
  rhs.root = null;
}

private Node<AnyType> merge(Node<AnyType> h1, Node<AnyType> h2) {
  // 任意一颗树为空，直接返回另外一颗树即可，无需其他操作
  if (h1 == null) { return h2; }
  if (h2 == null) { return h1; }

  // 将大的树插入到小的树中
  if (h1.element.compareTo(h2.element) < 0) {
    return merge1(h1, h2);
  }
  return merge1(h2, h1);
}

private Node<AnyType> merge1(Node<AnyType> h1, Node<AnyType> h2) {
  // 如果左子树为空，直接插入即可
  if (h1.left == null) {
    h1.left = h2;
  } else {  // 左子树不为空，沿着右路径到右子树，重复前面的合并操作
    h1.right = merge(h1.right, h2);
    // 更新零距离，并通过交换左右子树来维持左倾堆的特性
    if (h1.left.npl < h1.right.npl) {
      swapChildren(h1);
    }
    // 依据左倾堆的特性，节点的零距离由右子树决定
    h1.npl = h1.right.npl + 1;
  }
}

private void swapChildren(NodeType<AnyType> t) {
  Node<AnyType> tmp = t.left;
  t.left = t.right;
  t.right = tmp;
}

插入

有了合并，插入就再简单不过了，就是将当前堆与只有一个节点的堆进行合并

public void insert(AnyType x) {
  root = merge(new Node<>(x), root);
}

查找最值

前面提到，左倾堆并没有改变普通堆的元素值的特性，根节点依旧是全局最值，直接返回即可

public AnyType findMin() {
  if (root == null) { return null; }

  return root.element;
}

删除最值

通过前面的例子我们也知道最值在根节点，删除最值就是删除根节点。当根节点被移除，当前堆其实就变成了左右两个小堆。而左倾堆的特性适用于堆中的任意一个节点，也就是说，这两个小堆也是左倾的，这样的话我们直接将两个堆合并即可

public AnyType deleteMin() {
  if (isEmpty()) {
    throw new UnderflowException();
  }

  AnyType minItem = root.element;
  root = merge(root.left, root.right);

  return minItem;
}

时间复杂度分析

前面的操作中，你可以看到，除了查找最值，其他的操作都是借助合并操作来达成的。因而，我们只需要分析合并操作的时间复杂度即可。合并操作是一个递归向下的过程，具体点就是沿着堆的右路径向下，右路径的长度就直接决定了时间复杂度。关于左倾堆，有如下结论：

• 假设左倾堆最右边路径上有 x 个节点，那么整颗树最少有 $ 2^r - 1 $ 个节点

这个结论可以通过数学归纳法证明，证明如下：

• 如果 r = 1，结论明显成立。假设 r = 2，r = 3 , … ,r = k, 结论均成立，我们需要证明 r = k + 1 时结论也成立。如果一颗树的右路径上有 k + 1 个节点，那么去到右子树，其右路径上有 k 个节点，套前面的结论，右子树最少有 $ 2^k - 1 $ 个节点才能维持其左倾的特性。再来看左子树，依照左倾堆的特性，左节点的零距离必定不小于右节点的，因而左子树的右路径至少也要有 k 个节点才能保证这个特性。最后，加上根节点，总共的节点个树就是： \((2^k - 1) + (2^k - 1) + 1 = 2^{k+1} - 1\)

结论证明成立

也就是说，如果一个左倾堆有 N 个节点，那么它的右路径最多有 logN 个节点。换句话说，合并的时间复杂度是 O(logN)，插入以及删除最值的时间复杂度也是 O(logN)。