堆的优化：二项堆

Posted Oct 4, 2023

By Yuhang Peng 22 min read

普通堆存在的问题

在前面一篇文章中，我们介绍了堆，准确地说是二叉堆，这是最简单也是最基础的堆结构。它可以在 O(1) 的时间获取最值，其它各项操作时间复杂度均为 O(logN)。

普通堆有什么问题？难道这些操作还可以更快？先不急着思考如何优化，让我们来看一个案例。在实际场景中，我们经常需要做的一件事是合并两个数据集，比如将两个数组进行合并，将两个集合进行合并等等。堆也不例外，想象一下，如果我们要合并两个二叉堆，该如何做，时间复杂度又会是多少？

最直接也最容易想到的方案是将一个堆中的元素挨个插入到另一个堆中，比如将元素少的堆中的元素插入到元素多的堆中，时间复杂度就是 O( min(N1,N2) * log(max(N1,N2)) )。

除了上面这种方式，我们也可以按照构建堆的方法来进行堆的合并，整个操作时间复杂度是 O(N1 + N2)。

不管用哪种合并方法，最后所产生的时间开销肯定是比堆的常规操作的 O(logN) 来得大。如果还想进一步提高，我们势必要对堆的结构做一些调整。

二项堆是什么

普通堆之所以会带来比较大的时间开销是因为所有的元素都在一个树上，特别是像合并这类操作，我们很难不去考虑整个树。那有没有可能我们可以把一个树拆成多个树？

二项堆就是基于这个思路来进行优化，二项堆是一个树的集合，也就是森林。那么具体是怎样的呢？

我们还是用数组来表示整个二项堆，数组中的每个元素就是一颗树的根节点。在此基础上，二项堆有如下规则：

每个位子上的树的元素个数必须是 $ 2^{i} $，其中 i 是树在数组的下标（起始是 0），比如数组第一个树的节点总数就必须是 1，第二个是 2，第三个是 4，以此类推
当有元素进入到二项堆中，选择构建单节点树，将其放置在数组第一个位置，如果位置上有其他的树存在，就进行合并，然后选择放到第二个位置去，在第二位置重复之前的操作

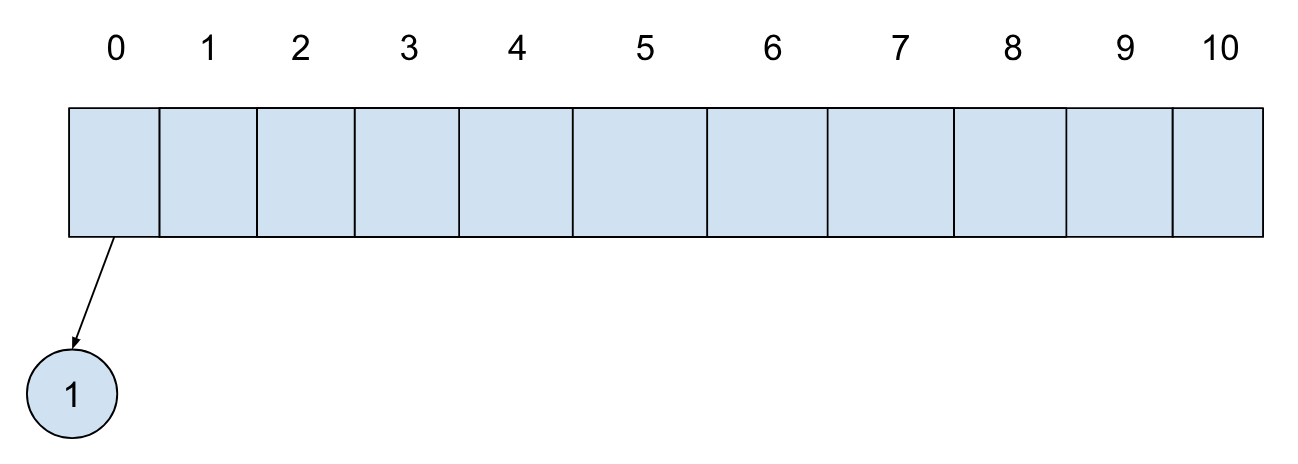
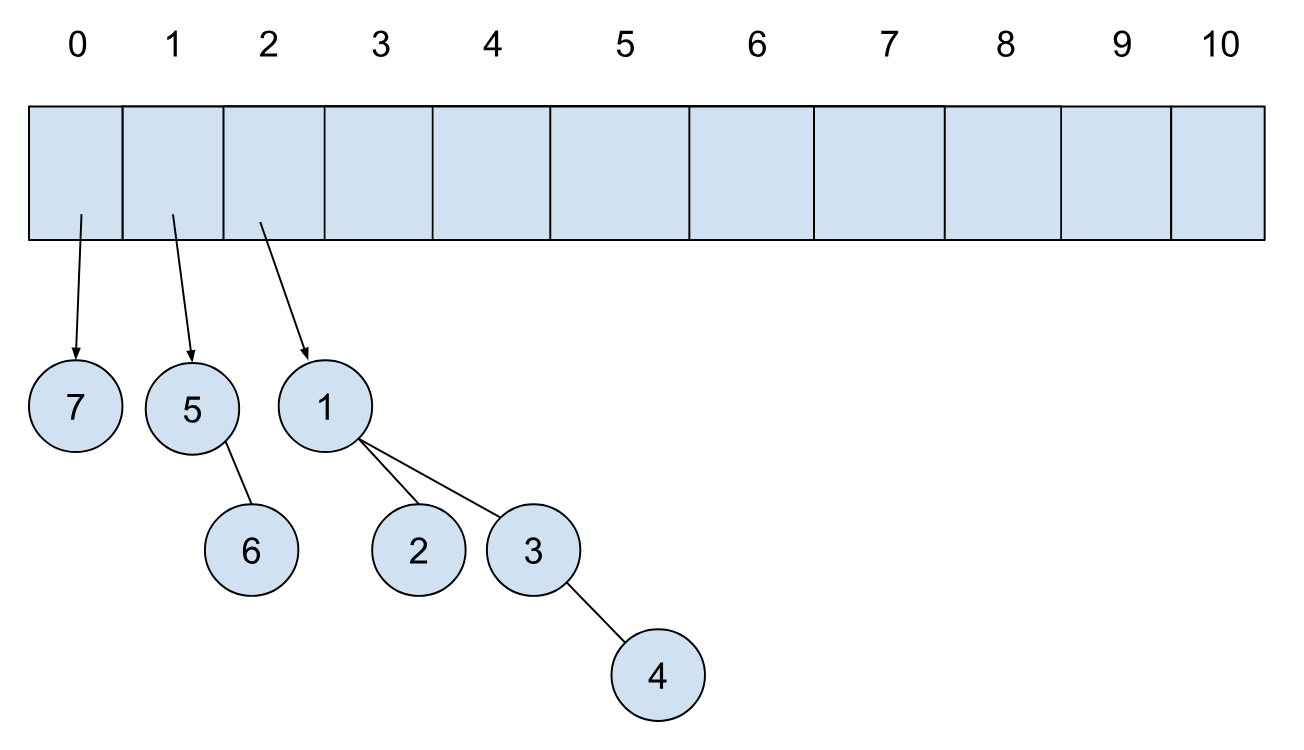
相信单凭语言很难理解，我们还是来直接看一个从零构建堆的过程：

第一个元素插入，构建单节点的树，此时数组为空，直接放置到数组第一个位置：

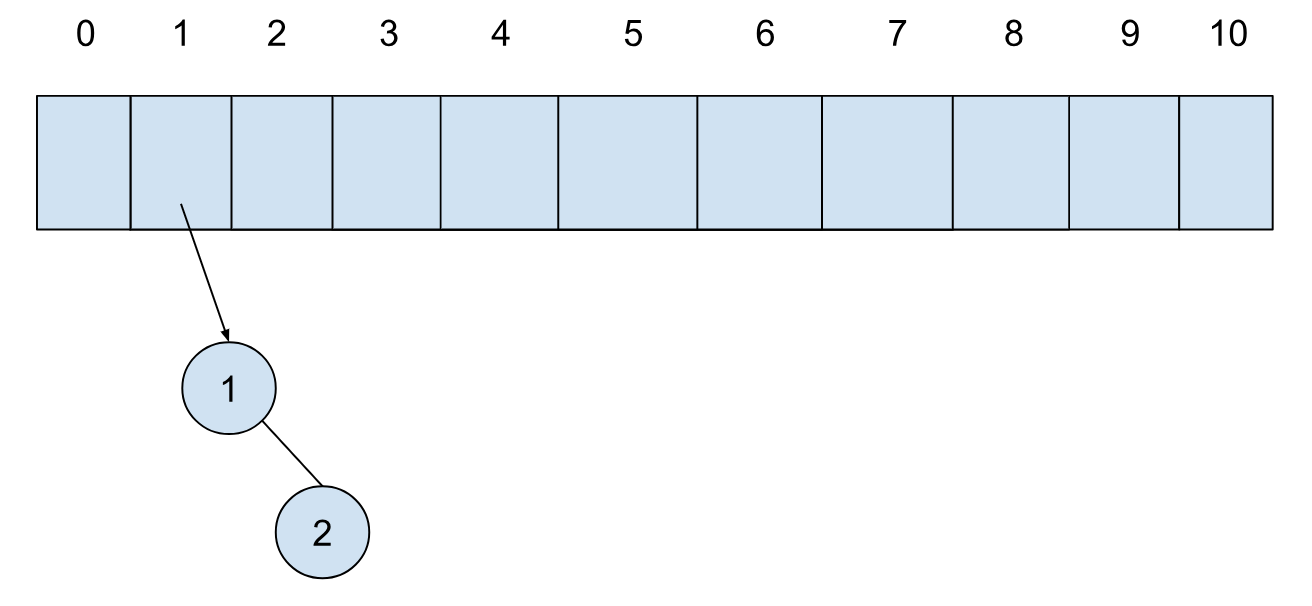
第二个元素进来时，构建单节的树，此时第一个位置有树，我们将其合并，并将合并后的树放置到后面一个位置（这里我们展示的是最小堆，合并要保证最小元素必须在根节点，两树合并其实就是把其中一个树当作另一个树根节点的子树，无需其他操作）：

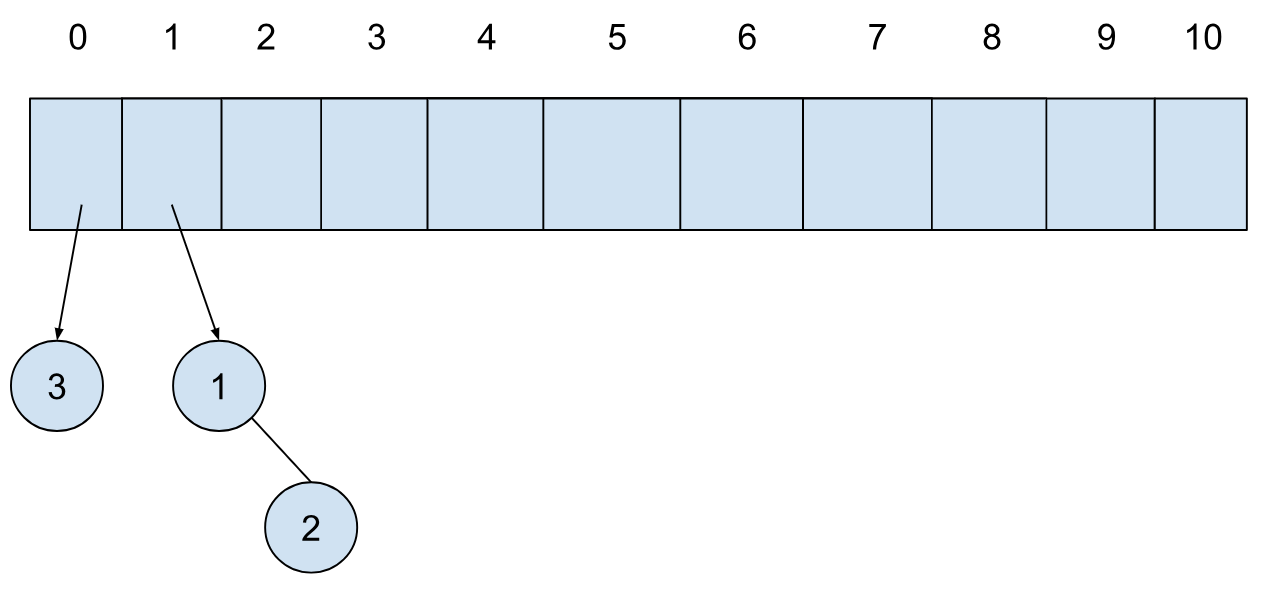
第三个元素插入，构建单节点的树，此时数组第一个位置为空，直接放置：

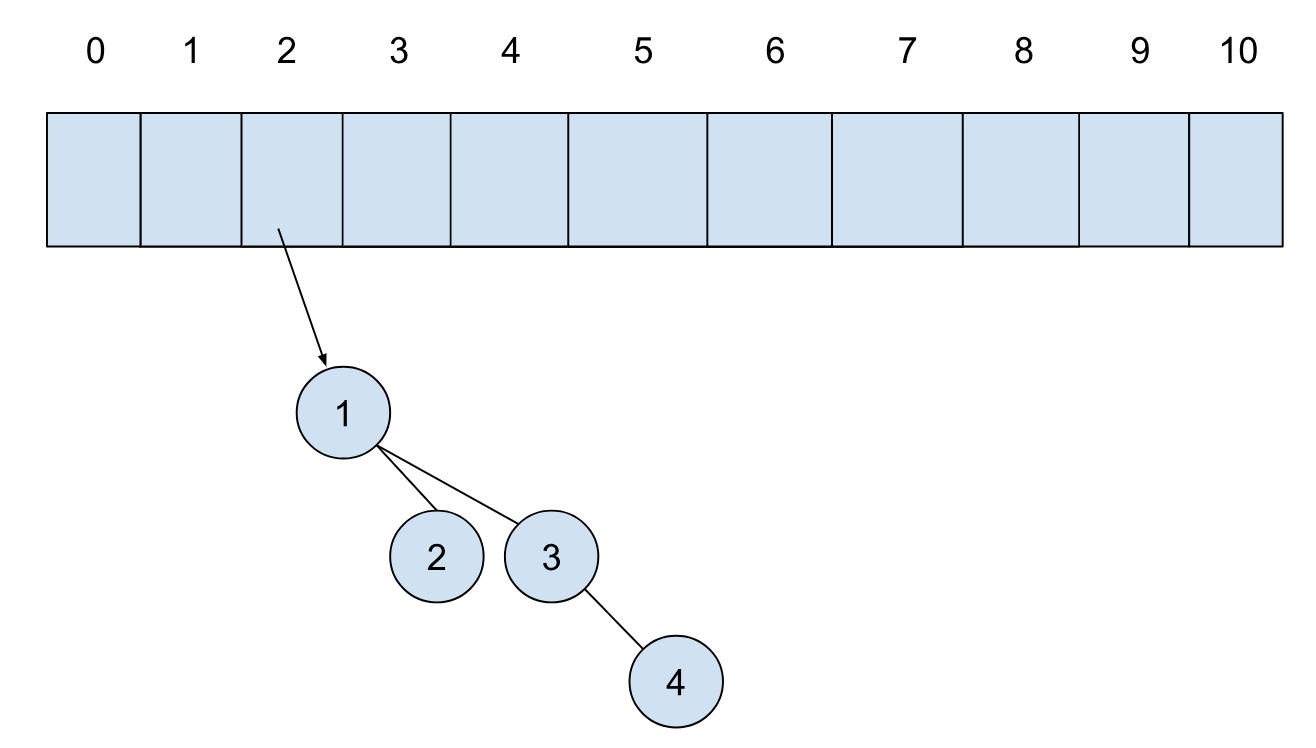
第四个元素插入，构建单节点的树，此时第一个位置有树，我们将其合并，放置到第二个位置的时候发现第二个位置也有树，继续合并，将合并后的树放置到第三个位置：

我们接着插入三个元素，操作完成后，堆的结构如下：

从上面这个例子可以看出，二项堆其实和二进制整数很像。每一位代表 $ 2^{i} $ 的值，插入其实就是在原数的基础上加 1。合并就是两个整数做加法。这么想，也就很能理解二项堆这个名字的由来。

二项堆的操作

我们之前提到普通堆的操作，在二项堆中是如何进行的呢？时间复杂度又是多少？我们挨个来看。在此之前，我们要先定义一下二项堆的节点：

  
private static class Node<AnyType> {
  // Constructors
  Node(AnyType element) {
    this(element, null, null);
  }

  Node(AnyType element, Node<AnyType> lt, Node<AnyType> nt) {
    this.element = element;
    leftChild = lt;
    nextSibling = nt;
  }

  AnyType  element;
  Node<AnyType> leftChild;
  Node<AnyType> nextSibling
}

你可能会觉得奇怪，不是说一个节点可以有多个子节点吗？为什么只定义了两个子节点？

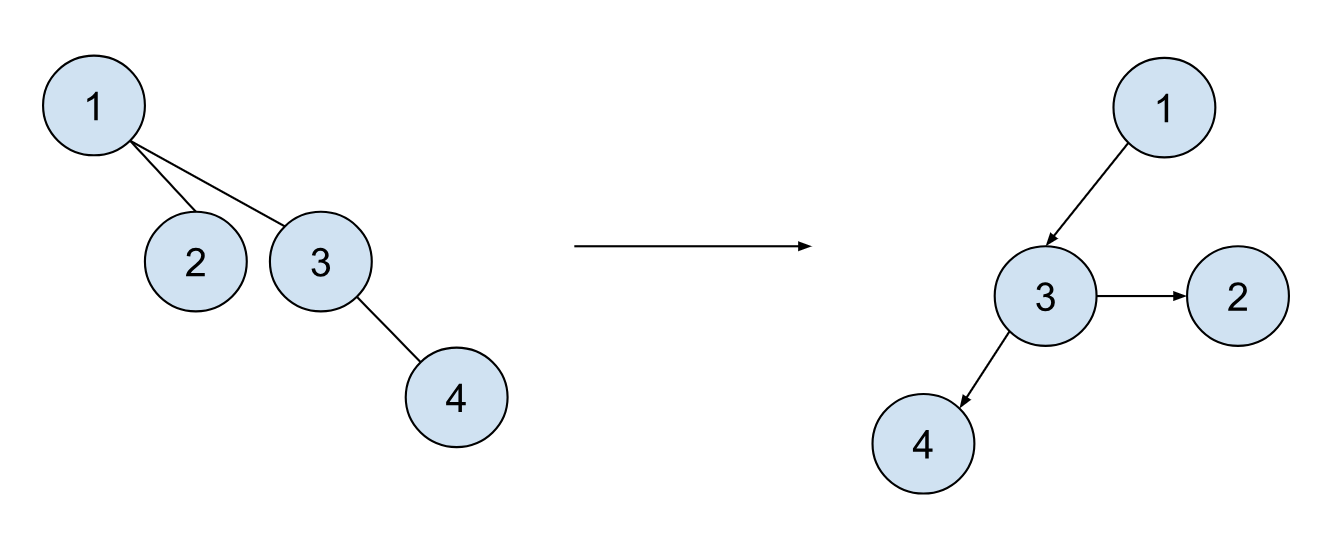
这里主要是为了后面的操作，因为链表的删除，更改以及交换节点位置等操作会比数组来的高效。如果按照上面的实现，之前的例子中第三个位置的树就长成下面这样：

当 1 被删除，按照右图的实现方式，我们可以还原合并之前的两颗树，3-4，以及 2（1 被删除后只剩下单节点）。这种定义规则下，根节点没有同级的节点，两树合并也相当的简单，具体实现如下：

  
private Node<AnyType> combineTrees(Node<AnyType> t1, Node<AnyType> t2) {
  // 因为实现的是最小堆，确保最小的节点为根节点
  if (t1.element.compareTo(t2.element) > 0) {
    return combineTrees(t2, t1);
  }
  t2.nextSibling = t1.leftChild;
  t1.leftChild = t2;
  return t1;
}

合并

首先要考虑的一个操作就是合并，因为这是其他操作的基础。之前说过，二项堆的合并有点像二进制整数相加。假设有 t1，t2 两个二项堆，我们从低位开始依次对每位上的树进行合并，合并后只会留有 t1 一个二项堆，在合并过程中会有如下几种情况：

t1 的合并位为空，t2 的合并位也为空，这种情况不用做任何操作
t1 的合并位不为空，t2 的合并位为空，这种情况不用做任何操作
t1 的合并位为空，t2 的合并位不为空，这种情况只需把 t2 中的树转移到 t1 中
t1 的合并位不为空，t2 的合并位不为空，这种情况需要合并，合并后的树存放在 carry 变量中（表示进位）
t1 的合并位为空，t2 的合并位也为空，carry 不为空，这种情况直接将 carry 中的树转移到 t1 中
t1 的合并位为空，t2 的合并位不为空，carry 不为空，这种情况和 4 类似，将 t2 和 carry 变量中的树合并并存放在 carry 变量中
t1 的合并位不为空，t2 的合并位为空，carry 不为空，这种情况和 6 中的操作类似，将 t1 和 carry 变量中的树合并并存放在 carry 变量中
t1，t2，carry 变量均不为空，这种情况将 carry 变量转移到 t1 中，t1，t2 合并后的树放入 carry 变量里

代码实现如下：

  
public void merge(BinomialQueue<AnyType> rhs) {
  if (this == rhs) {
    return;
  }

  currentSize += rhs.currentSize;

  if (currentSize > capacity()) {
    int maxLength = Math.max(theTrees.length, rhs.theTrees.length);
    expandTheTrees(maxLength + 1);
  }

  Node<AnyType> carray = null;
  for (int i = 0, j = 1; j <= currentSize; i++, j *= 2) {
    Node<AnyType> t1 = theTrees[i];
    Node<AnyType> t2 = i < rhs.theTrees.length ? rhs.theTrees[i] : null;

    int whichCase = t1 == null ? 0 : 1;
    whichCase += t2 == null ? 0 : 2;
    whichCase += carray == null ? 0 : 4;

    switch(whichCase) {
      case 0:   // 情况 1
      case 1:   // 情况 2
        break;
      case 2:   // 情况 3
        theTrees[i] = t2;
        rhs.theTrees[i] = null;
        break;
      case 3:   // 情况 4
        carry = combineTrees(t1, t2);
        theTrees[i] = rhs.theTrees[i] = null;
        break;
      case 4:   // 情况 5
        theTrees[i] = carry;
        carry = null;
        break;
      case 5:   // 情况 6
        carry = combinTrees(t1, carry);
        theTrees[i] = null;
        break;
      case 6:   // 情况 7
        carry = combinTrees(t2, carry);
        rhs.theTrees[i] = null;
        break;
      case 7:   // 情况 8
        theTrees[i] = carry;
        carry = combineTrees(t1, t2);
        rhs.theTrees[i] = null;
        break;
    }
  }

  for (int k = 0; k < rhs.theTrees.length; k++) {
    rhs.theTrees[k] = null;
  }
  rhs.currentSize = 0;
}

一个元素个数为 N 的二项堆，它的树的个数是 logN，合并仅仅是对树的操作，每次树的合并的时间复杂度均为 O(1)，因此最后二项堆的合并操作的时间复杂度为 O( log(max(N1, N2)) )，可见与二叉堆的合并相比，的确要快不少。

插入

有了合并操作，插入操作其实就是由单一元素构建一个二项堆，然后将构建好的二项堆合并到原来的二项堆中去。代码实现如下：

  
public void insert(AnyType x) {
  merge(new BinomialQueue<>(x));
}

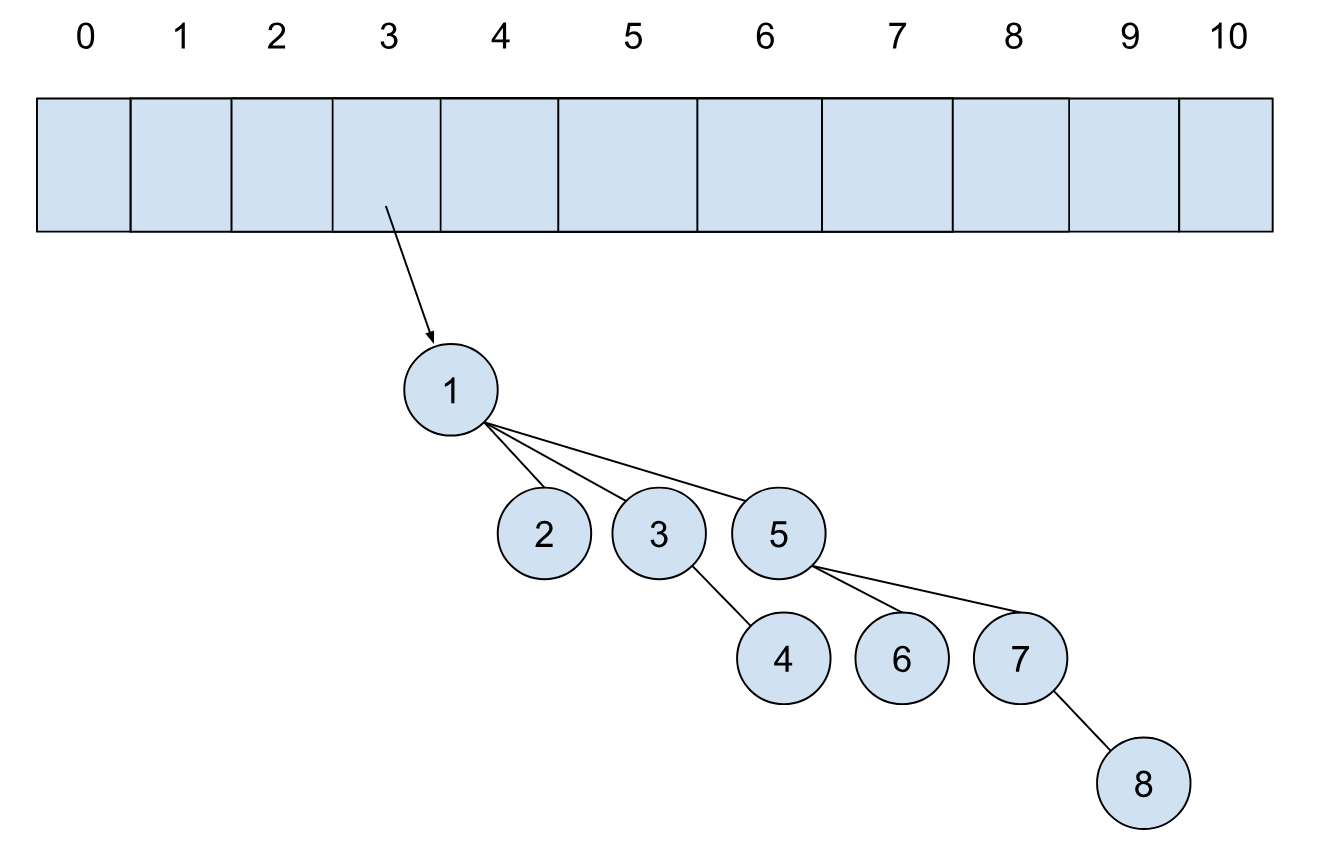
插入操作的难点主要在时间复杂度的分析，如果说是最差时间复杂度，那么肯定毫无疑问是 O(logN)。但是最差时间复杂度有时并不能说明问题，这是因为前一次的插入会对后一次造成影响，比如我们将一个元素插入到下面这个堆中：

这里我们每个位都得进行合并，时间复杂度是 logN，但是插入完成后，二项堆长这样：

下一次的插入时间复杂度就会是 O(1)，这里我们需要考虑 均摊时间（Amortized Time），也就是连续多个操作时间叠加再求平均的时间复杂度（区别于平均）。那么我们怎么确定这个均摊时间是多少呢？

可以观察到的是，当一个操作花费 c 单位的时间，就会在合并范围内增加 2 - c 颗树，比如上面的例子第一次合并就花了 4 个单位的时间，但最后 3 颗树变成了 1 颗，这为后面合并节省了时间。

我们假设第 i 次插入花费了 $ C_i $ 单位的时间，插入后起始连续的树的个数为 $ T_i $，最开始二项堆为空，也就是 $ T_0 = 0 $，根据上面的观察，我们有：

\[(T_i - T_{i-1}) = 2 - C_i\]

也就是：

\[C_i + (T_i - T_{i-1}) = 2\]

假设我们连续插入 N 个元素，于是就有下面这些等式：

\[C_1 + (T_1 - T_0) = 2\] \[C_2 + (T_2 - T_1) = 2\] \[C_3 + (T_3 - T_2) = 2\] \[...\] \[C_{N-1} + (T_{N-1} - T_{N-2}) = 2\] \[C_{N} + (T_{N} - T_{N-1}) = 2\]

将上述所有等式相加就可以得到：

\[\sum_{i=1}^NC_i + T_N - T_0 = 2N\]

所以，插入 N 个元素的操作总花费为：

\[\sum_{i=1}^NC_i = 2N - (T_N - T_0)\]

其中 $ T_N - T_0 >= 0 $，所以

\[\sum_{i=1}^NC_i <= 2N\]

可见，平均每个插入操作的均摊时间为 O(1)。

查找最值

既然二项堆并不由一颗树构成，而是由 logN 颗树构成，并且最小值可能在任意树的根节点，那么是不是说这个操作的时间复杂度退化到了 O(logN)？其实我们完全可以进行优化，无非是用一个变量来存放最值元素所在的树的位置，每次增改操作后都将这个值进行更新即可，这样一来，我们就可直接定位到最值，时间复杂度还是 O(1)。

删除最值

这个操作也非常直接，思路就是，先定位到最值所在的树，然后将整颗树从二项堆中移除，并将这颗树根节点下面一层的子树重新构建一个新的二项堆，再将这个二项堆合并到原来的二项堆中去

代码实现：

  
public AnyType deleteMin() {
  if (isEmpty()) {
    throw new UnderflowException();
  }

  int minIndex = findMinIndex();
  AnyType minItem = theTrees[minIndex].element;

  Node<AnyType> deletedTree = theTrees[minIndex].leftChild;

  // 由被删除的根节点的子树构建新的二项堆
  BinomialQueue<AnyType> deletedQueue = new BinomialQueue<>();
  deletedQueue.expandTheTrees(minIndex + 1);

  deletedQueue.currentSize = (1 << minIndex) - 1;
  for (int j = minIndex - 1; j >= 0; j--) {
    deletedQueue.theTrees[j] = deletedTree;
    deletedTree = deletedTree.nextSibling;
    deletedQueue.theTrees[j].nextSibling = null;
  }

  // 将最值对应的树移除
  theTrees[minIndex] = null;
  currentSize -= deletedQueue.currentSize + 1;

  // 将两个堆合并
  merge(deletedQueue);

  return minItem;
}

这个操作因为需要合并，并且删除的节点不固定，最差的时间复杂度是 O(logN)。当然了，这个过程中还会有 O(logN) 空间的消耗。

总结

二项堆是基于二叉堆演变而来，但是它在某些操作上会比二叉堆更加高效：

操作	二项堆	二叉堆
合并	$ O(logN) $	$ O(N) $
插入	$ O(1) $ (均摊)	$ O(logN) $
找最值	$ O(logN) $ (可优化到 $ O(1) $)	$ O(1) $
删除最值	$ O(logN) $	$ O(logN) $

完整代码实现:

  
public class BinomialQueue<AnyType extends Comparable<? super AnyType>> {
  private static final int DEFAULT_TREES = 1;
  private int currentSize;
  private Node<AnyType>[]

  public BinomialQueue() {}
  public BinomialQueue(AnyType item) {}

  private int capacity() {
    return (1 << theTrees.length) - 1;
  }

  private int findMinIndex() {
    if (isEmpty()) {
      throw new UnderflowException();
    }

    int minIndex;
    AnyType minElement == null;
    for (int i = 0; i < theTrees.length; i++) {
      if (theTrees[i] == null) {
        continue;
      }
      if (minElement == null || minElement.compareTo(theTrees[i].element) < 0) {
        minElement = theTrees[i].element;
        minIndex = i;
      }
    }
    return i;
  }

  private Node<AnyType> combineTrees(Node<AnyType> t1, Node<AnyType> t2) {
    // 因为实现的是最小堆，确保最小的节点为根节点
    if (t1.element.compareTo(t2.element) > 0) {
      return combineTrees(t2, t1);
    }
    t2.nextSibling = t1.leftChild;
    t1.leftChild = t2;
    return t1;
  }

  public void merge(BinomialQueue<AnyType> rhs) {
    if (this == rhs) {
      return;
    }

    currentSize += rhs.currentSize;

    if (currentSize > capacity()) {
      int maxLength = Math.max(theTrees.length, rhs.theTrees.length);
      expandTheTrees(maxLength + 1);
    }

    Node<AnyType> carray = null;
    for (int i = 0, j = 1; j <= currentSize; i++, j *= 2) {
      Node<AnyType> t1 = theTrees[i];
      Node<AnyType> t2 = i < rhs.theTrees.length ? rhs.theTrees[i] : null;

      int whichCase = t1 == null ? 0 : 1;
      whichCase += t2 == null ? 0 : 2;
      whichCase += carray == null ? 0 : 4;

      switch(whichCase) {
        case 0:   // 情况 1
        case 1:   // 情况 2
          break;
        case 2:   // 情况 3
          theTrees[i] = t2;
          rhs.theTrees[i] = null;
          break;
        case 3:   // 情况 4
          carry = combineTrees(t1, t2);
          theTrees[i] = rhs.theTrees[i] = null;
          break;
        case 4:   // 情况 5
          theTrees[i] = carry;
          carry = null;
          break;
        case 5:   // 情况 6
          carry = combinTrees(t1, carry);
          theTrees[i] = null;
          break;
        case 6:   // 情况 7
          carry = combinTrees(t2, carry);
          rhs.theTrees[i] = null;
          break;
        case 7:   // 情况 8
          theTrees[i] = carry;
          carry = combineTrees(t1, t2);
          rhs.theTrees[i] = null;
          break;
      }
    }

    for (int k = 0; k < rhs.theTrees.length; k++) {
      rhs.theTrees[k] = null;
    }
    rhs.currentSize = 0;
  }

  public void insert(AnyType x) {
    merge(new BinomialQueue<>(x));
  }

  public AnyType findMin() {
    int index findMinIndex();
    return theTrees[index].element;
  }
  
  public AnyType deleteMin() {
    if (isEmpty()) {
      throw new UnderflowException();
    }

    int minIndex = findMinIndex();
    AnyType minItem = theTrees[minIndex].element;

    Node<AnyType> deletedTree = theTrees[minIndex].leftChild;

    // 由被删除的根节点的子树构建新的二项堆
    BinomialQueue<AnyType> deletedQueue = new BinomialQueue<>();
    deletedQueue.expandTheTrees(minIndex + 1);

    deletedQueue.currentSize = (1 << minIndex) - 1;
    for (int j = minIndex - 1; j >= 0; j--) {
      deletedQueue.theTrees[j] = deletedTree;
      deletedTree = deletedTree.nextSibling;
      deletedQueue.theTrees[j].nextSibling = null;
    }

    // 将最值对应的树移除
    theTrees[minIndex] = null;
    currentSize -= deletedQueue.currentSize + 1;

    // 将两个堆合并
    merge(deletedQueue);

    return minItem;
  }

  public boolean isEmpty() {
    return currentSize == 0;
  }
}

日志, 算法, 堆

算法堆

This post is licensed under CC BY 4.0 by the author.