图：找关键点

Posted Oct 21, 2023

By Yuhang Peng 10 min read

图上的关键点（articulation points）

我们之前介绍过图的基本概念，我们知道如果一个图是连通的，表明图上任意的一个节点都可以通过遍历来访问到图上的其他节点。

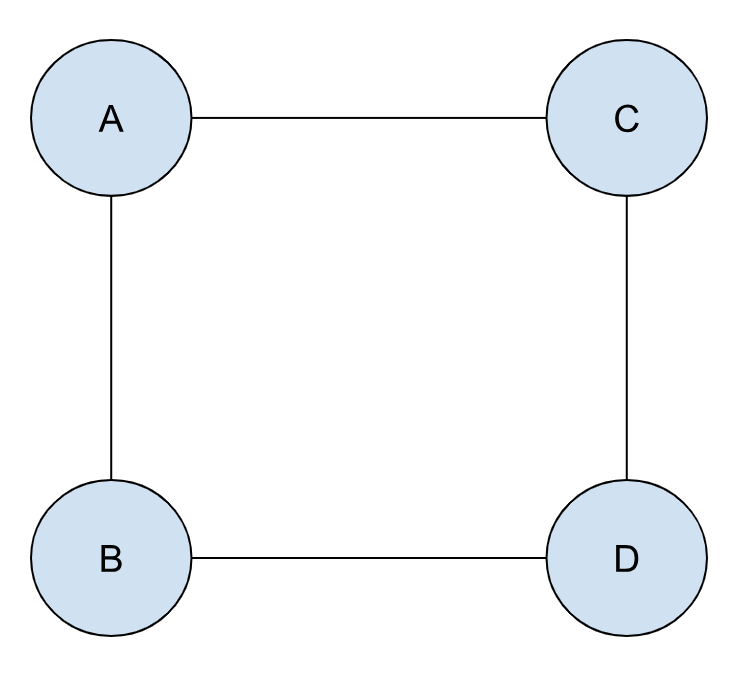
在此基础上，我们在做一下延伸，在一个连通图中，如果移除任意一个节点都不会破环其连通性，那么这个的图就被称为 双向连通的（biconnected）。比如下图就是一个双向连通图：

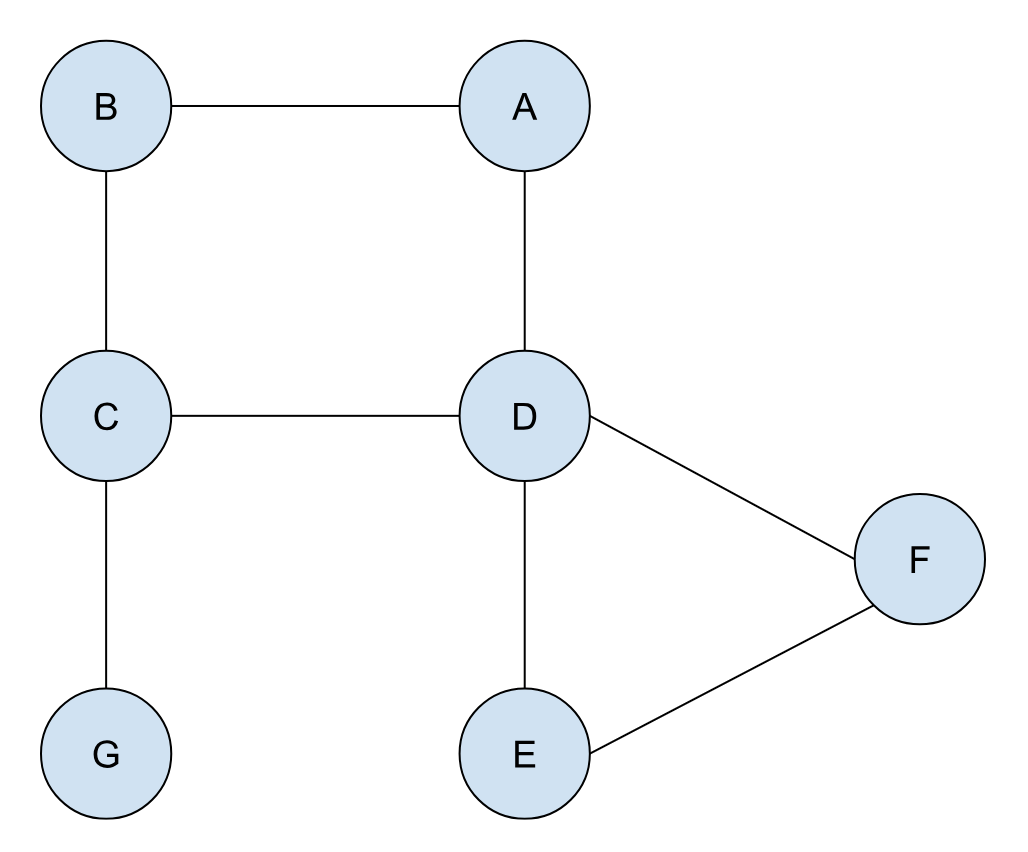
这和我们今天讲的东西有什么联系？要知道双向连通这个要求是比较严苛的，那么对于那些不是双向连通的图，我们就需要清楚哪些地方，或者说哪些节点的移除会导致图不再连通，这样的节点就被称为 关键节点（articulation points）。比如下图中的 C 以及 D 就是关键节点：

C 的移除会导致节点 G 与原图脱离，D 的移除会导致节点 E 以及 F 与原图脱离。

找关键节点有什么实际的意义？这里你可以把节点想象成是网络中的路由，道路中的枢纽，以及机场或是火车站，公交站，关键节点的缺失势必会造成图上一部分的节点和其余节点脱离，这是我们不希望看到的。找到关键节点，对其进行严格保护以及监控预警才会让整个系统更加地稳定。

具体算法

那么如何找呢？通过观察，可以发现那些关键节点本身的特征并不明显，但是与其相连的节点要想互联，那么就只能经由它。比如上面的例子中的 C，与其相连的 G 要想去到其他节点，那么就必须经由 C。

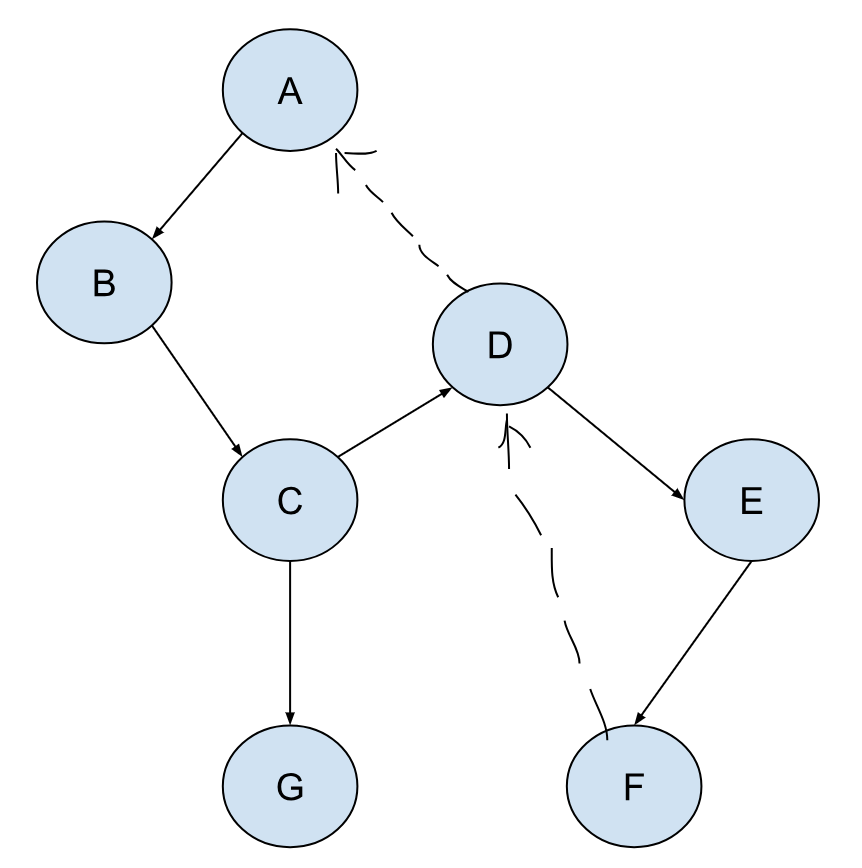
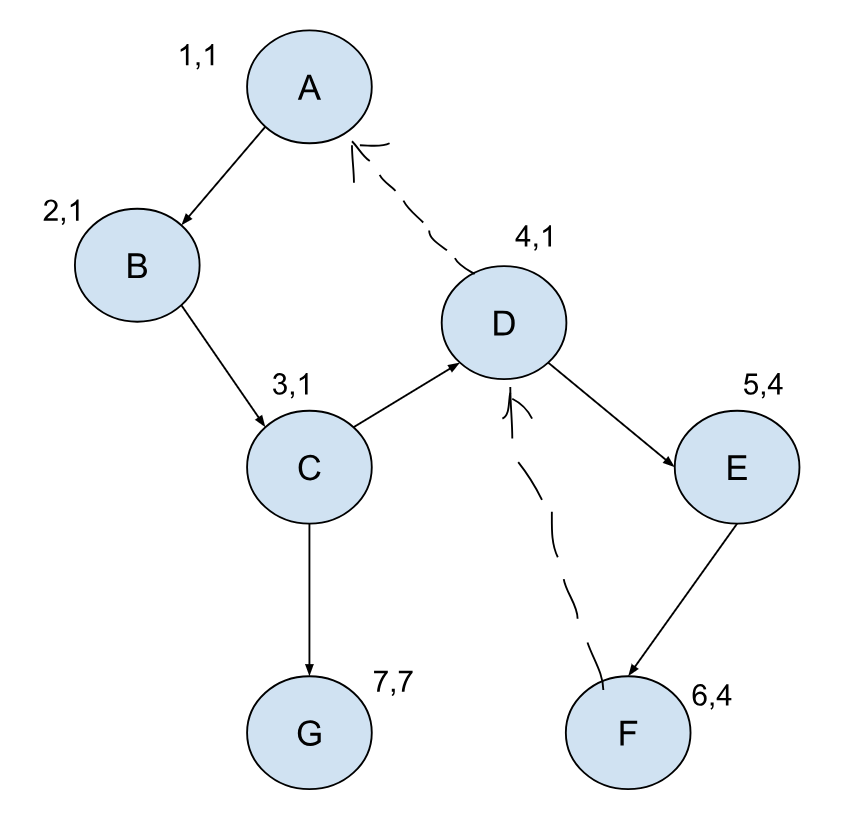
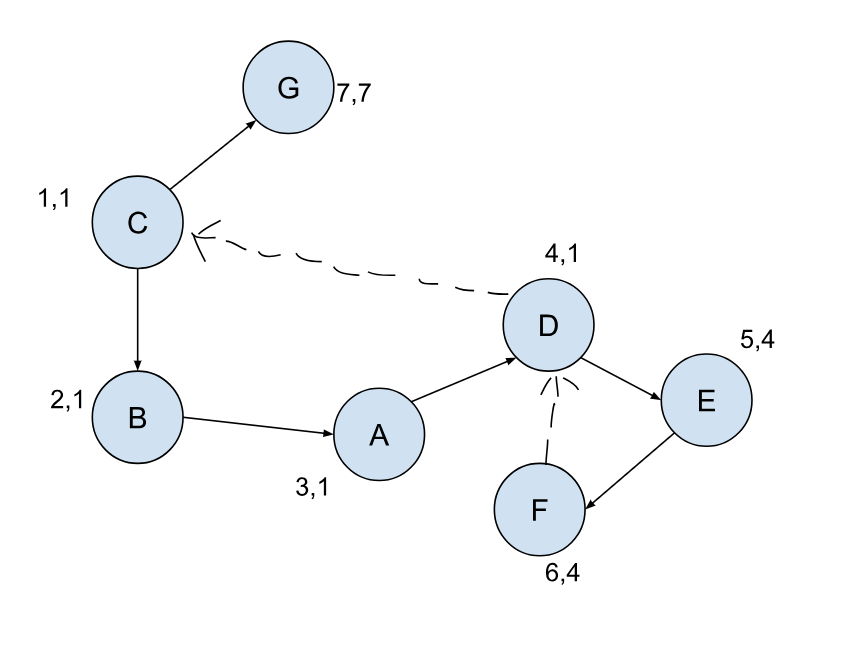
但这些都只是直观上的感受，如何把其落实到实际的算法中呢？图的问题一般都是通过遍历来解决，如果我们用深度优先搜索来遍历这张图，我们其实可以得到一个类似树的结构：

图上的实线是遍历的路径，同样的节点我们不需要进行二次遍历。虚线表示的是 返回路径，表明现在正在遍历的节点是有另外一条路径通到之前遍历过的节点（父节点除外，因为这其实是同一条边），这个信息对我们寻找关键点很重要。

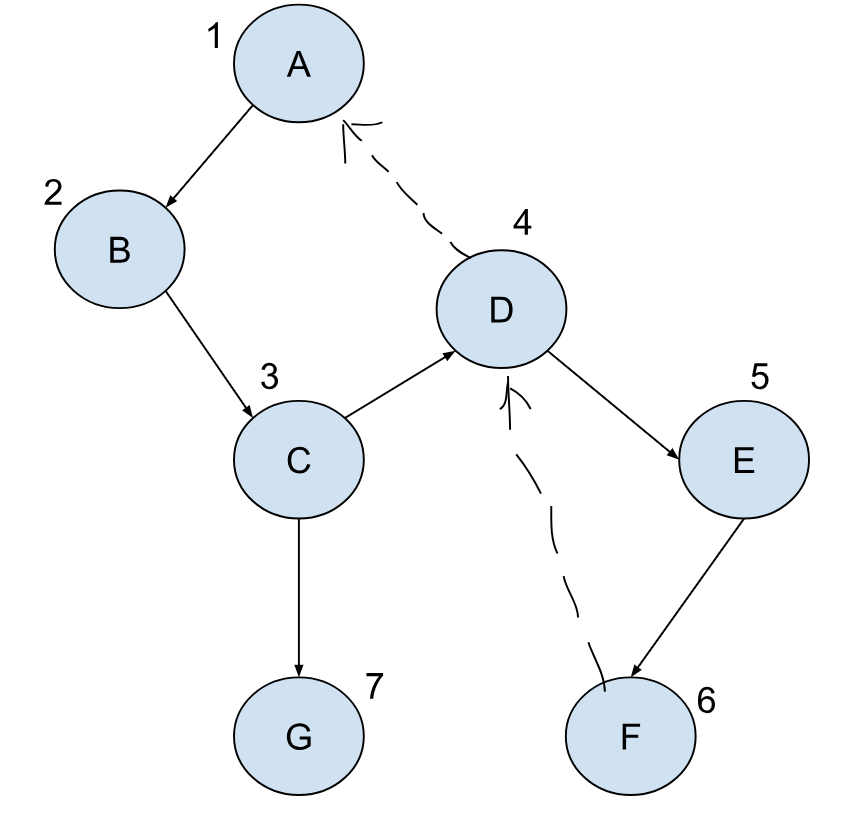
我们按照遍历的顺序从小到大给每个节点都填上编号：

如果把这个图看作是树，那么这样的编号方式其实是 前序遍历，也就是每到一个节点我们就编号。

有了这个编号还不够，我们的目的是找到一个节点是否可以连通到其他的节点。从图中可以很容易地观察到，如果一个节点不管是通过返回路径，或是其他路径能够通到其父节点之外的节点，那么说明该节点很可能有其他的通路。

我们这里给每个节点再定义一个最小路径编号，至于为什么是最小，我们待会再说，它是下面这些编号取最小值：

节点编号
所有返回路径上的节点编号
所有路径中的节点的最小路径编号

最小路径编号依然可以通过遍历得到，我们将其列在编号的后面：

如果还是把这个图看作是树，这个遍历就是 后序遍历，每个节点的编号都需要依赖其子节点的结果，因而节点的编号在其子节点之后。

最小路径编号可以告诉我们什么呢？通过比较一个节点的编号与其子节点的最小路径编号，我们就可以知道该节点是不是关键节点。如果子节点的最小路径编号比该节点的编号小，说明子节点可以通过其他的路径通到前面遍历过的节点，所以即使该节点被移除，那么子节点也不会受影响（因为有通路可以避开该节点），反之，说明子节点并没有其他的路径来避开该节点，那么这个该节点就是关键节点。

当然，有个例外就是根节点，也就是遍历最开始的点，它的编号肯定是最小的，如果按照上面的方法，其子节点的最小路径编号不可能比它还小。因此对根节点来说，除了要用上面的方法进行检验外，我们还需要看它是不是有多个子节点，如果仅有一个子节点，那么即使把它移除，其余图依然连通，它就不是关键节点。反之，如果根节点有两个或者两个以上的子节点，则表明其是关键节点，比如我们从节点 C 开始遍历，我们就需要这个检测：

算法具体实现如下

  
class Vertex {
  Vertex parent;
  List<Vertex> adjacents;
  boolean visited;
  int num; // 节点编号
  int low; // 最小路径编号
}

class Graph {
  private int counter = 1;

  // 前序遍历算出每个节点的编号
  public void assignNum(Vertex v) {
    v.num = counter++;
    v.visited = true;
    for (Vertex n : v.adjacents) {
      if (!w.visited) {
        w.parent = v;
        assignNum(w);
      }
    }
  }

  // 后序遍历计算最小路径编号，找到关键节点
  public void assignLow(Vertex v) {
    v.low = v.num;  // 1. 节点编号
    for (Vertex n : v.adjacents) {
      if (w.num > v.num) {
        assignLow(w);
        if (w.low >= v.num) {
          System.out.println(v + " is an articulation point");
        }
        v.low = Math.min(v.low, w.low);  // 3. 所有路径中的节点的最小路径编号
      } else if (v.parent != w) {     // 返回路径
        v.low = Math.min(v.low, w.num);  // 2. 所有返回路径上的节点编号
      }
    }
  }

  public void findArt(Vertex v) {
    assignNum(v);
    assignLow(v);

    // 对根节点进行额外的检测
    int numOfChildren = 0;
    for (Vertex n : v.adjacents) {
      if (n.parent == v) {
        numOfChildren++;
      }
    }

    if (numOfChildren > 1) {
      System.out.println(v + " is an articulation point");
    }
  }
}

上面是把前序和后序遍历分开来进行，合在一起也是可行的：

  
void findArt(Vertex v) {
  v.visited = true;
  v.low = v.num = counter++;  // 1. 节点编号
  for (Vertex n : v.adjacents) {
    if (!w.visited) {
      w.parent = v;
      findArt(w);
      if (w.low >= v.num) {
        System.out.println(v + " is an articulation point");
      }
      v.low = Math.min(v.low, w.low);  // 3. 所有路径中的节点的最小路径编号
    } else if (v.parent != w) {     // 返回路径
      v.low = Math.min(v.low, w.num);  // 2. 所有返回路径上的节点编号
    }
  }
}

因为要遍历图上的所有节点和路径，时间复杂度是 O(V + E)

日志, 算法, 图

算法图

This post is licensed under CC BY 4.0 by the author.

图上的关键点（articulation points）

具体算法

Trending Tags