图上的最短路径：Dijkstra

图的基本概念

在开始今天的内容之前，我们先来弄清楚两个问题，“图是什么？”，“图又有哪些表示形式？”。

同链表和树一样，图也是由两个东西组成————节点（vertices）和边（edges）。与图不同的是，链表和树都会对其边做一些限制，比如对普通单链表来说，每个节点一一首尾相连，一眼看过去，链表就是一个线性结构。树的话在链表的基础上放宽要求，比如二叉树的每个节点可以有两个子节点，但是一般说来，和单链表一样，树的边也是有方向性的（父 ——> 子）。

链表和树都是对节点以及边做了些限制而得到，我们可以说链表是图，也可以说树是图，图是链表和树之上更宽的一个概念。一个图可以表示成 G = (V, E)，其中 V 表示节点，E 表示边。

这就完了吗？图的概念很广，链表是图，树是图，节点和边随随便便放在一起也是图，如果仅仅提到图，我们很难清楚这东西具体指什么，因此我们会对其细分。

要知道，不管是图、链表或是树，他们的节点都是一样的，不一样是对边的要求。根据对边的要求的不同，我们可以得到下面这些概念：

• 根据边是否具有方向性，我们可以将图分为 有向图（directed graph）和 无向图（undirected graph）
• 根据是否有环，我们可以将图分为有环图 和 无环图（acyclic graph），一般来说话默认可能有环
• 根据边是否带有权重，可以分为 有权图（weighted graph） 和 无权图（un weighted graph）。一般默认无权

上面着三个基本概念可以自由组合，比如被广泛提及的有向无环图——DAG(Directed Acyclic Graph)。

当然，图中还有一个 路径（path） 的概念，把它单独拆出来看就类似是一个链表。简单路径（simple path） 指的是除首尾节点外，路径上访问到的节点不能重复。

还有一个连通的概念，如果从图上任何一个节点出发，总是能访问其他所有节点，那么这个图就是 连通的（connected）。在有向图中，为了对这个概念细分，连通的图被称为 强连通（strongly connected）。如果一个有向图不是连通的，但是将其看成是无向图却是连通的话，那么这个有向图就是 弱连通（weakly connected）。完全图（complete graph） 的要求更加严格，表示任何一对节点之间都存在直接相连的边，当然这也是边最多的情况，拿无向图来说，这里 $ E = V(V-1)/2 $。

图上的最短路径问题

给定一个有向图 G = (V, E)，以及一个节点 s，我们需要找到 s 与其他任意节点之间的最短的路径（路径的长度是路径上所有边的权重之和）。

这个问题看似清晰明了，实则禁不起推敲，如果允许图有环并且允许边的权重为负的话，那么存在的一种情况是，一条路径无限次经过权重为负的边，这样最短路径可以到负无穷。我们必须做一些限制，要不就是图中没有权重为负的情况，要不就是当存在这种情况是最短路径为 0。

图上的最短路径算法

最短路径算法多种多样，今天我们要介绍的 Dijkstra 算法是其中最广为人知的一种，它背后的思想是 贪心。贪心的本质思想就是 局部最优可以扩展到全局最优，但要知道这个思想并不是任何时候都奏效，反证法是证明贪心无效的常见途径，也就是说你找到一种情况，局部最优没法推广到全局最优，那么就说明贪心无效，但是反过来，证明贪心有效往往不是那么容易，有时需要复杂的数学推导和证明。

当我们用 Dijkstra 来求最短路径是，还需要有一个前提————图中不能存在权重为负的边，否则的话，该算法求解出来的结果就会是错误的，至于原因我们后面会解释。

Dijkstra 算法的思想是，从起始节点开始，每到一个节点，标记已经访问，已经标记的节点将不再被访问，我们时刻记录到每个节点所需要的花费，如果此时没有遍历到某节点则表明花费为 ∞，我们每次都选择当下花费最小的节点作为下一个要标记的节点。

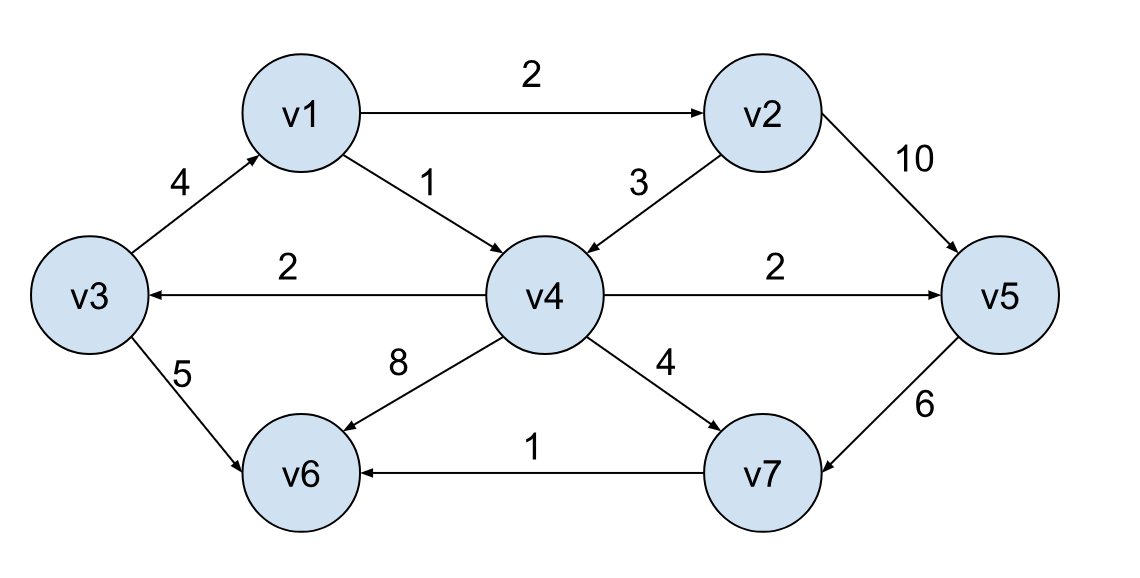
说的有点抽象，还是来举个例子：

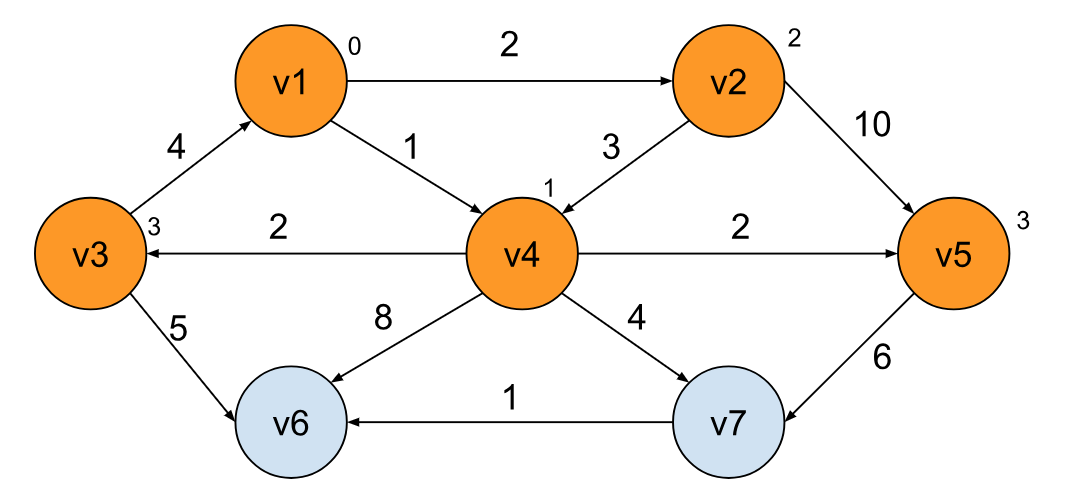
假设我们的起始节点为 v1，也就是说我们到 v1 的花费为 0:

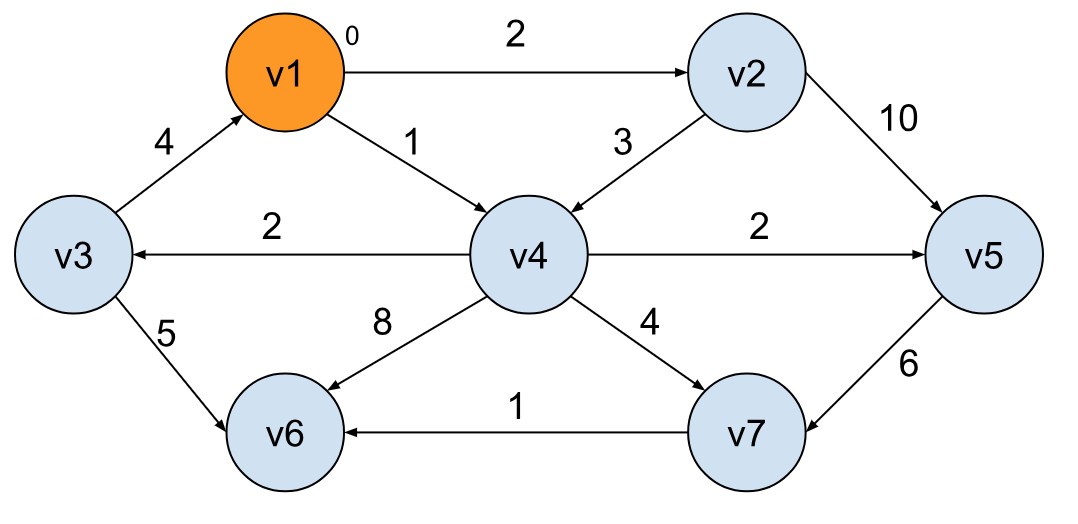
从 v1 为起点，我们可以到达 v4 和 v2，这里我们选择最小情况，也就是 v4：

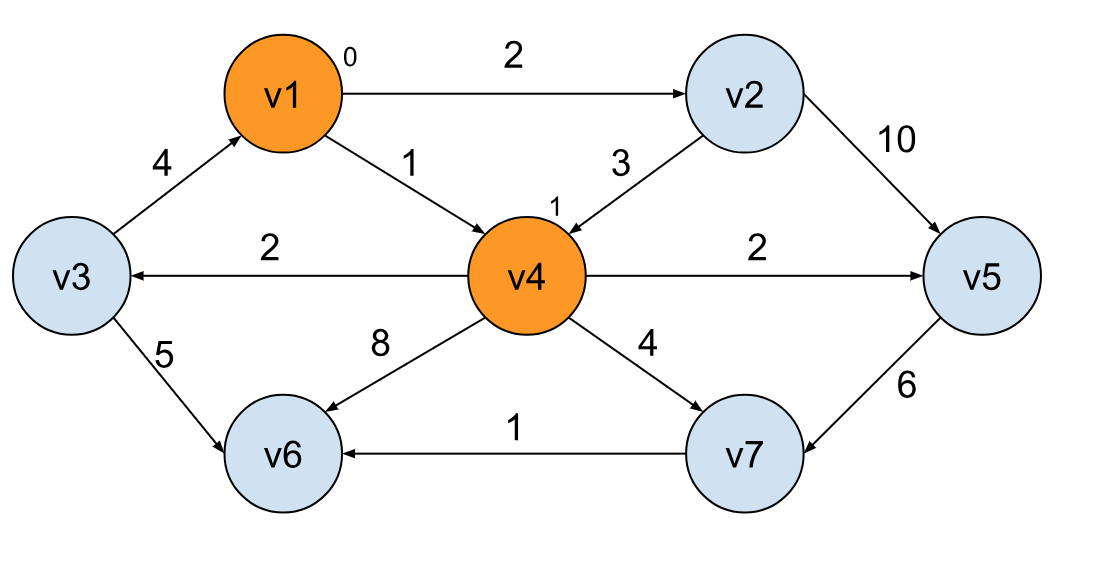
这时我们可以选择去到 v2，通过 v4 我们又可以去到 v5，v6，v7，v3，还是老样子，选择当前路径最短的点，去到 v2 只需要花费 0 + 2 的开销，为当前的最小：

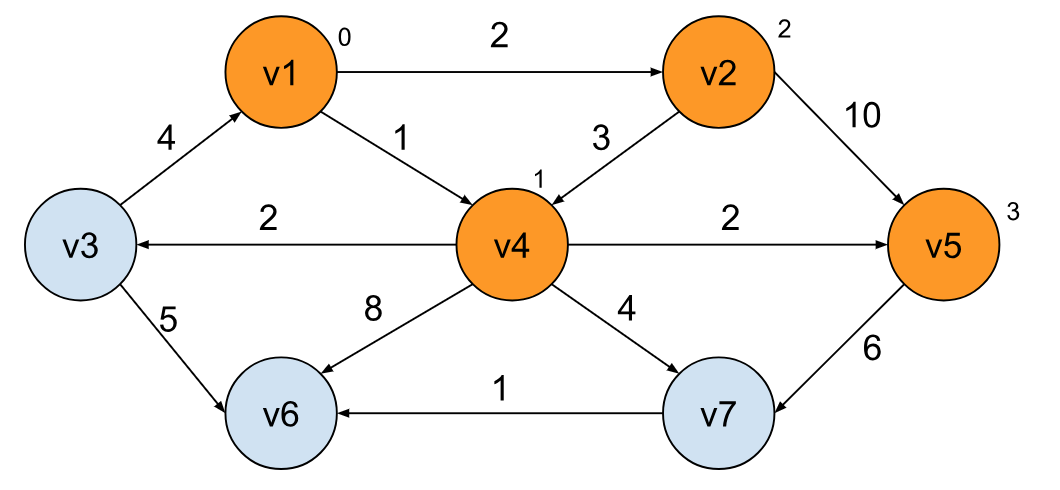
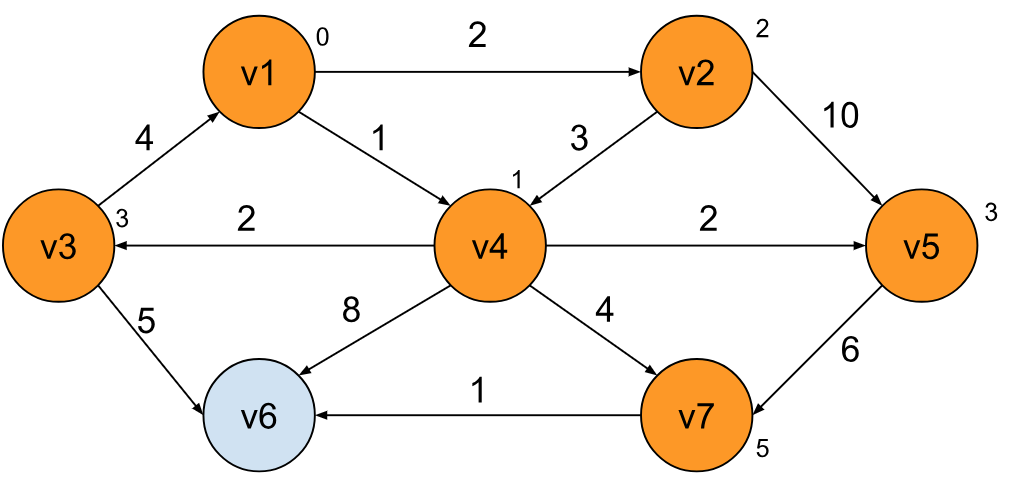
每到一个节点我们就将此节点标记起来，表明下次不会再访问，于此同时，通过这个节点我们可以解锁去到其他节点的路径，比如这里就解锁了 2 -> 5 的路径，但是我们需要选择最小开销，对比下来，还是 4 -> 5 的路径总开销比较小，为 1 + 2 = 3:

同样的策略，我们可以将 v3 标记并得出 v1 到 v3 的最短路径：

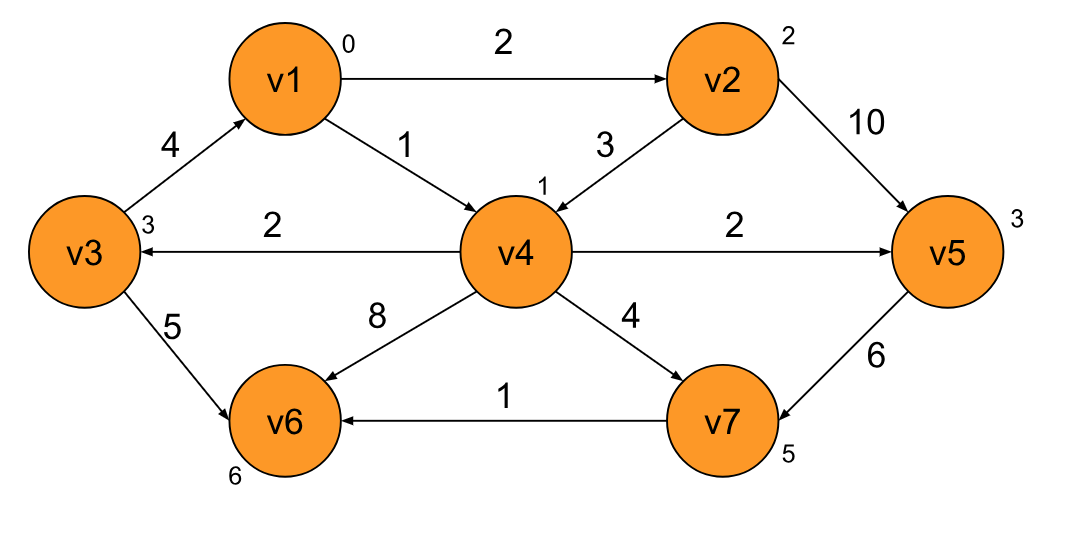
类似的方法，我们也可以得出 v1 到 v6，以及 v7 的最短路径：

整个算法跑完，我们就可以得出 v1 到任意节点的最短路径的值具体是多少，当然，如果有需要，你也可以将具体的路径给保存下来，方法和计算路径和类似。

最开始接触这个算法的时候，最为困惑的点在于如何证明这个算法的正确性？为什么这里的局部最优可以推广到全局最优？

假设我们的起始点为 $ V_s $，一开始的时候我们发现存在 $ V_s $ 到 $ V_t $ 的直接路径，怎么确定这个路径就一定是最短的？我们是否可以从 $ V_s $ 先到其他节点，然后再从其他节点再到 $ V_t $？如果当前所有 $ V_s $ 到其相邻节点的直接路径中，$ V_s $ 到 $ V_t $ 是最短的，那就排除了这种情况，因为从 $ V_s $ 到其他节点的开销已经超过了从 $ V_s $ 直接到 $ V_t $ 的开销，并且重点是图中没有负权重，那么即使有其他的路径，那这个路径也不会产生更低的开销。把这里的 $ V_s $ 换成是任意中间节点，也是一样的，只不过我们考虑的不再是单个边，而是路径和。因此，每次仅考虑当前最短的路径和就能保证最终的答案是最短的。

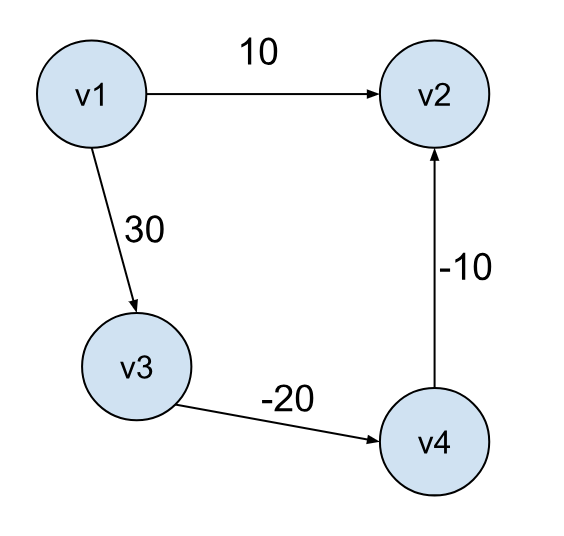
回到之前的问题，为什么图中有负权重存在的话，这个算法将不奏效。道理很简单，我们不能排除未知的路径，该路径会经过权重为负的边到达我们已标记的节点，让我们的结果变得不正确，比如下面这个例子：

如果起始节点是 v1，那么按照此算法，到 v2 的最短路径会被认为是 10，然而 v1 -> v3 -> v4 -> v2 的路径开销为 0。

由此可见，图中不含有负权重的边是 Dijkstra 算法成立的必要条件。

具体实现：

class Vertex {
  public Map<Vertex, Integer> adj;  // adjacency vertex to edge's weight
  public boolean visited;
  public int dist;
}

class VertexCompare implements Comparator<Vertex> {
  public int compare(Vertex s1, Vertex s2) {
    return s1.dist - s2.dist;
  }
}

void dijkstra(Vertex s, Vertex[] graph) {
  for (Vertex v : graph) {
    v.dist = Integer.MAX_VALUE;
    v.visited = false;
  }

  PriorityQueue<Vertex> pq = new PriorityQueue<>(
    new VertexCompare<Vertex>()
  );

  s.dist = 0;
  pq.add(s);

  while (!pq.isEmpty()) {
    Vertex cur = pq.poll();

    if (cur.visited) {
      continue;
    }

    cur.visited = true;
    for (Vertex n : cur.adj.keySet()) {
      if (!n.visited) {
        int cost = cur.adj.get(n);
        if (cur.dist + cost < n.dist) {
          n.dist = cur.dist + cost;
          pq.add(n);
        }
      }
    }
  }
}

在上面的实现中，我们利用了优先队列（堆），把每次找最小值的时间缩小至 O(logV)，其中 V 表示的是节点的个数。除了节点，我们还需要挨个遍历每个节点的边，假设边的个数是 E，由此可得算法的时间复杂度为 O(ElogV + VlogV) = O(ElogV)。

因为我们是通过边来确定是否将某节点加入到队列，也就是说队列中可能同时存在两个节点，因此空间复杂度是 O(E)。