为硬盘而生的数据结构:B 树
时间复杂度之外的复杂度
算法绕不开的一个概念就是时间复杂度,我们衡量一个算法的好坏基本上也就看这个指标。解同一个问题,$ O(N) $ 的做法就是会比 $ O(N^2) $ 要高效,要更节省时间。但是这里我们其实省略了一个前提条件,这些算法都是在内存中运行的。你可能会觉得奇怪,算法不在内存中运行还在其他地方运行吗?
内存属于计算机的内部存储资源,除此之外,计算机还会和外界存储设备打交道,比如各种硬盘。就拿磁盘来说,数据都是分区的,定位数据并返回数据的时延是很大的。现代计算机每秒钟能够执行 10 多亿条指令,但是每秒钟计算机只能和磁盘建立不到 1000 次交互。
可见这里的时间瓶颈已经不再是算法时间复杂度了,而是计算机与磁盘进行数据交互的次数。我们之前常常说的平衡二叉树,比如 AVL,Splay 还有红黑树都是在内存中运行的,但你试想一下,假如每个树节点的数据都是存放在磁盘中的,那么上述这些数据结构还能提供高效的搜索吗?
很显然,场景变了,如何节省时间的数据结构也需要改变。
B 树结构介绍
正如上面所说,当数据(树)存放在磁盘上,从根节点开始树的搜索遍历,每往下一层跳到一个新的树节点,就代表着要进行一次磁盘的读取,那么树的高度或层数越小,我们访问磁盘的频率就会越低。
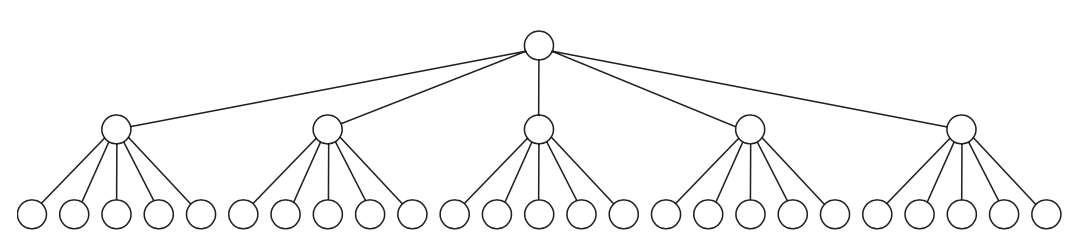
之前我们讨论的树的算法大都在内存中,而且都是以二叉树为主,这也是为什么时间复杂度是和 $ log_2N $ 相关的。这里我们需要缩小树的高度,而且需要保证所有数据都在树上,那么唯一的方法就是通过增加树的宽度来降低树的高度,也就是将之前的二叉树改为 M 叉树,比如下图显示的是 M = 5 的情况:
这颗树上一共有 31 个节点,有 3 层,但如果是二叉树,那么则需要 5 层。树的层数 H 和节点数 N 的关系为 $ H = log_MN $。
但是 M 叉树还不是最终的 B 树,它仅仅是 B 树的一个基本框架,还有很多的数据存放上的细节。关于 B 树,也不止一个版本,B 树前前后后演变了很多次,现在主流的都是 B+ 树。关于 B 树和 B+ 树,这里对二者的区别不做深究,就都当成是 B 树,我们来看看 B 树在 M 叉树结构上做了哪些限定:
- 所有的数据都存放在叶子节点
- 非叶子节点最多存放
M - 1个 Keys 来帮助搜索定位 - 根节点可以是叶子节点,也可以有 2 ~ M 个子节点
- 所有的非叶子节点(根节点除外)的子节点数量必须在 ⌈M/2⌉ 和 M 之间
- 所有的叶子节点存放的数据条数必须在 ⌈L/2⌉ 和 L 之间(L 是基于节点的数据块大小与 M 计算得来)
这里的前 3 点都很好理解,而 4,5 两点主要是为了保证数据分布均匀而做的限定。和其他的数据结构一样,我们对 B 树也可以进行插入和删除操作,当数据多到不够放,那么我们就需要增加层数,反过来,但数据不断变少,我们则需要减少层数以提升效率,有了 4,5 两点的加持,我们让这两个过程更加地合理且稳定,在后面的例子中也会作具体讲解。
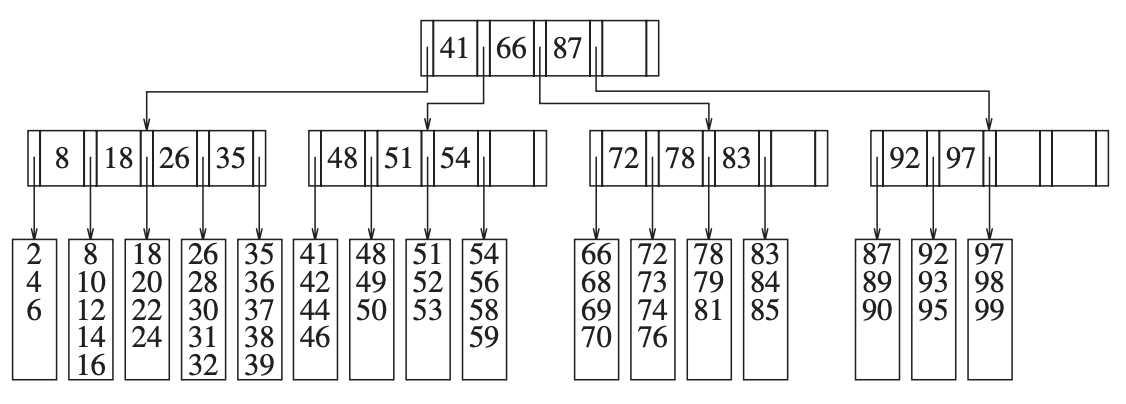
下图显示的是一个 M = 5,L = 5 的 B 树:
B 树上的操作
插入
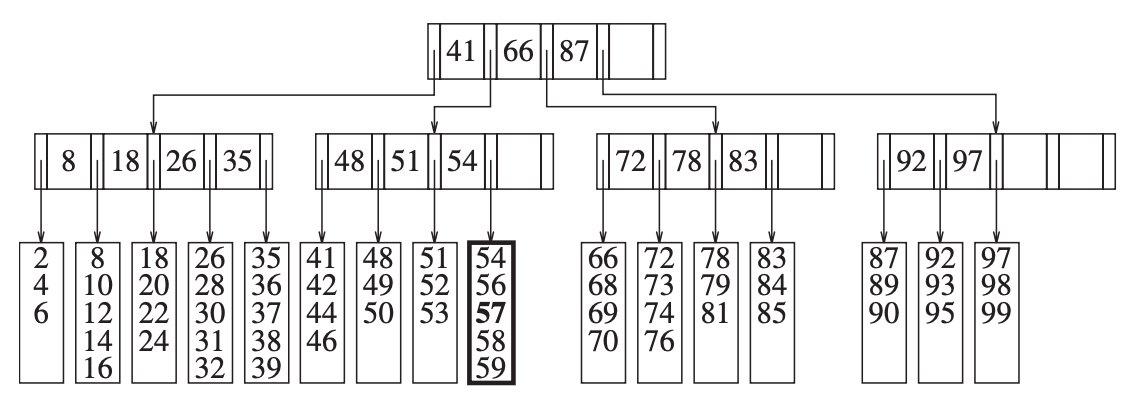
插入可谓是非常常见的操作,比如在上面的例子中插入 57 这个数据,我们就可以由上而下将数据放到对应的叶子节点上:
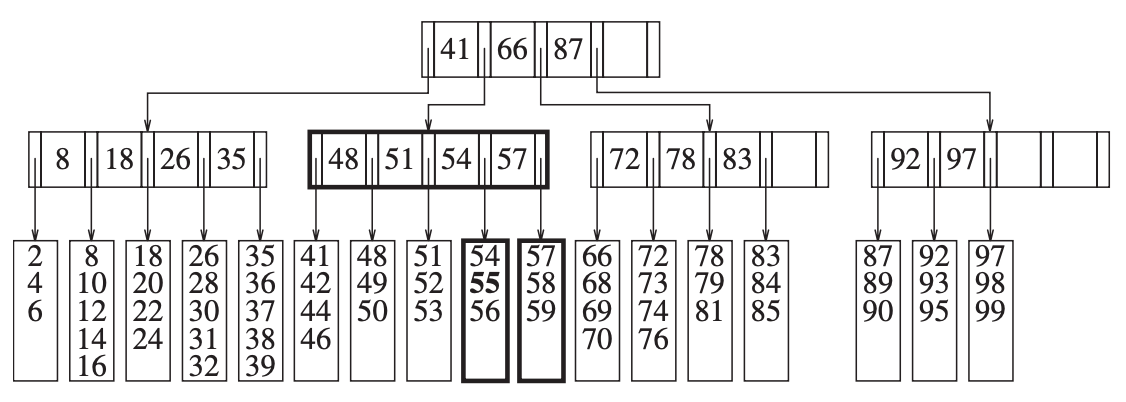
但是在插入中存在一些特殊的情况,比如当某个叶子节点的数据槽放满了,我们该如何处理呢?比如这里我们继续插入 55,这时这个数据槽的数据就会从 5 个变成 6 个,违反了之前的第 5 条限定,这时就需要将这个数据槽拆分,一般来说都是均等拆分,也就是拆分成两个大小为 3 的数据槽:
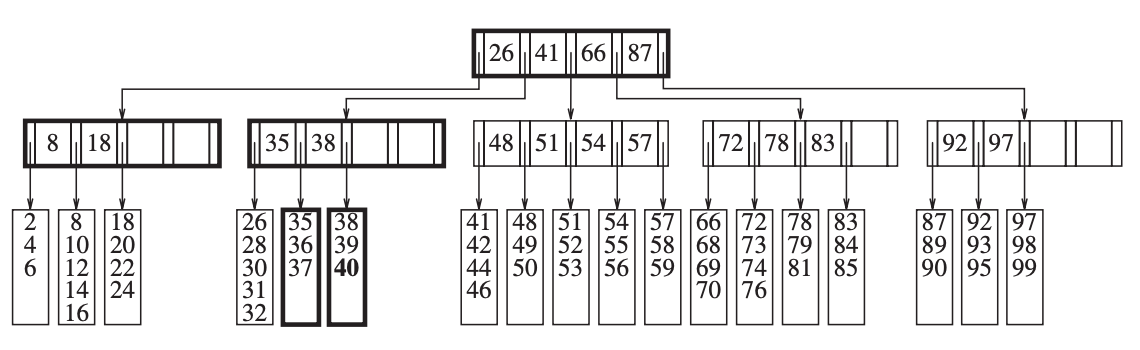
那如果说,叶子节点的父节点的 key 的上限到了呢?比如我们继续插入 40,这时,对应的叶子节点数据槽已满,我们按上个例子进行数据槽的拆分,但是叶子节点的父节点已经有 5 个子节点了,这时就违反了之前的第 4 条限定,那么这个时候就需要将父节点进行拆分,拆分成两个节点,每个节点带 3 个叶子节点:
由此可见,当某个节点存放的数据到了上限,我们只需要将这个节点存放的数据进行拆分,然后在它的父节点中新增一个 key 即可。如果它的父节点也达到了上限,那么就继续向上传递,将它的父节点也进行拆分,然后继续在祖父节点上新增一个 key,直到根节点。
如果发现根节点存放的数据也达到了上限,就将根节点一分为二,再向上增加一个新的根节点,这也就会导致 B 树的层数增加。
新增叶子节点数据槽,新增非叶子节点的 key 均会产生额外的磁盘读取,但是这些情况往往十分罕见,特别是在 M 和 L 比较大的情况下。这就类似动态数组的扩容,哈希表中的 rehashing,虽然单次操作的时间消耗很大,但是均摊到每次操作来看,其实微乎其微。
删除
删除其实就是插入的逆向操作,也就是将对应的数据移出数据槽。插入中的特殊情况需要我们对节点进行拆分,而删除就需要我们对节点进行合并。
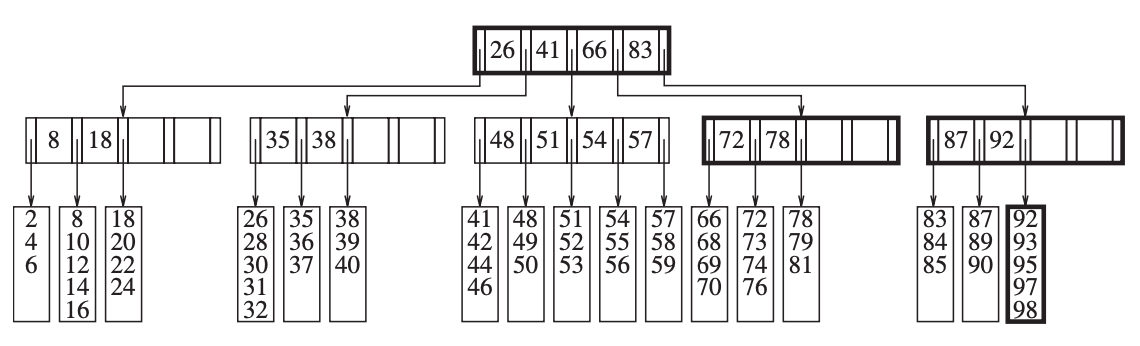
继续前面的例子,当我们要移出元素 99,你会发现数据槽中的数据个数变成了 2,小于 ⌈L/2⌉,这时就需要将相邻的数据槽中的数据移到当前数据槽中,如果相邻数据槽的数量也不够了,那说明这两个数据槽是可以合并的,直接进行合并。如果合并之后父节点的 key 的数量小于 ⌈M/2⌉,使用同样的策略即可,由此,删除操作后的树就是下面这样:
和插入操作的拆分类似,合并也是递归向上的,当合并导致根节点的子节点的数量小于 2,也就是根节点只有一个子节点,那么就可以移除之前的根节点了,这也就会导致 B 树的层数的减少。